
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие бинарного отношения.Содержание книги Поиск на нашем сайте
Операции над бинарными отношениями. Теоретические вопросы; Определение n - местного, одноместного (унарного), бинарного, тернарного отношений. Примеры унарного, бинарного, тернарного отношений. Способы задания бинарного отношения. Объединение, пересечение, разность, дополнение бинарных отношений. Обратное бинарное отношение. Композиция бинарных отношений. Докажите: композиция бинарных отношений не коммутативна, ассоциативна. 9. 1. Бинарное отношение r задано высказывательной формой. Задайте его: а) парами б) таблицей. 1. А = {-1, 0, 1, 2, 3} а, r в Û а + в Î 2Z 2. А = {n Î N, n £ 10}, а, r, в Û в = rеst (а, 4). 3. А = {-2, -1, 1, 2, 5}, а, r, в Û а + в ³ 0 ® а > в. 4. А = {-1, 0, 1, 2, 4, 5}, а r в Û а простое число). 9.2. a, b, n Ì 1. a = 3. х a у Û у = 2х + 5, х b у Û у = 3х + 5,
n = {(1; 0), (2; 1),(3; 2), (4; 1), (5; -5)}
4. х a у Û у = 9.3. Заданы отношения a = b на А = {-1,0,2,-3,3}. Найдите a Ç b, a 1. х a у Û х + у < 0, х b у Û х у £ 0, 2. х a у Û х + у х b у Û х, у простое число взаимно простые 3. х a у Û х = у 4. х a у Û х 9. 4. Для любых отношений a, b, n, заданных на множестве А, докажите: 1. (a È b) 3.(a) 5. (a Ç b) 6. (a È b) о n=(a о n) È (b о n), 7. (a Ç b) о Ì (a о n) Ç (b о n) 8. a о (bÇn) Ì (aоb) Ç (aоn). 9. (a \ b)о n É (a о n) \ (b о n), 10. a о (b \ n) É(a о b) \ (a о n).
З А Н Я Т И Е № 10. Свойства бинарных отношений. Теоретические вопросы: Запишите свойства бинарных отношений: рефлексивность, cимметричности, транзитивности, антирефлекcивности, антисимметричности, связности. Запишите, что означает - свойство нерефлексивности, несимметричности, нетранзитивности, несвязности. Является ли свойство антирефлекcивности отрицанием свойства рефлексивности, а свойство антисимметричности отрицанием свойства симметричности? 10. 1. Пусть r - бинарное отношение на множестве А. Докажите: 1. r = симметрично Û r 3. r - антирефлексивно Û r Ç D = Æ, 4. r - антисимметрично Û r Ç r 5. r - связно Û r Ì r 6. r - рефлексивность Û
10. 2. Выясните, двумя способами будет ли бинарное отношение r, заданное на множестве А = {1,2,3,} обладать свойствами рефлексивности, симметричности, транзитивности, антисимметричности, связности, если 1. r = {(1, 1),(1, 2),(2, 1),(2, -2),(3, 3),(2, 3)} 2. r = {(2, 1),(2, 2),(1, 2),(3, 3),(3, 2),(2, 3)} 3. r = {(2, 1),(2, 3)} 4. r = {(1, 2),(2, 3),(1, 3),(2, 1),(1, 1),(2, 2)} 5. r = {(2, 1),(3, 2),(3, 1),(1, 1),(2, 2),(3, 3)} 6. {(1, 1)}. 10. 3. Какими свойствами обладает отношение r 1. х r у Û х £ у + 1 на Z 2. х r у Û 2х + у 3. Х r У Û Х Ç У = Æ на Р(Z) 4. х r у Û у = | х| на R. 5. х r у Û х 10. 4. Какими свойствами обладают отношения: 1. Параллельности на множестве прямых на плоскости. 2. Перпендикулярности на множестве прямых на плоскости 3. Подобия на множестве всех многоугольников. 4. Х r У Û Х симметрична У относительно прямой Х, У - точки, не принадлежащие 5. “Быть родственником” на множестве людей. 6. “Быть знакомым” на множестве людей. 7. “Быть студентом одной группы” (одноклассником) на множестве всех людей. 10.5 Найдите смежный класс 1. х r у Û 3х + у 2. х r у Û х > 2у на N, а = 10, 3. х r у Û 4. х r у Û lg у = х 5. х r у Û |3х + 2| > у на R, а = 5. 10.6. Докажите: для любых отношений a и b, заданных на множестве А: 1. Если a, b - симметричны, то 2. Если a, b- рефлексивны, то a 3. Если a, b - транзитивны, то a Ç b, a 4. Если a, b антирефлексивны, то a È b, a Ç b - антирефлексивны. 5. Если a, b рефлексивны, то 6. Если a, b - антисимметричны, то a Ç b - антисимметричны.
З А Н Я Т И Е № 11. Отношение эквивалентности Теоретические вопросы: Определение отношения эквивалентности. В каком случае бинарное отношение не будет отношением эквивалентности? Понятие разбиения множества, класса эквивалентности, фактор-множества.
11.1. На множестве А = {1, 2, 3, 4, 5} задано отношение a. Найдите фактор множество А | a. Какие из заданных отношений будут отношениями эквивалентности? 1. a = 2. a = 3. a = 4. 5. a = 6. = 7. a = 8. a = 11. 2. Докажите, что М - разбиение множества А = {1,2,3,4,5,6,7} Перечислите все элементы отношения эквивалентности r соответствующего разбиению М.
1. М = {{1}, {2,5},{3}, {4,6,7,}}, 2. М= {{1,7},{2,4,5,6},{3}},
3. М= {{1,2,3,4,5,6,7}}, 4. М= {{ 1}, { 2}, { 3}, {4},{5},{6}, {7}}
5. М= {{1,2,4,},{5,6,7,} {3}, 6. M= {{1,2,3,4,},{5,6,7,}} 11. 3. Докажите, что r отношение эквивалентности. Найдите классы эквивалентности. 1. Х r У Û Х и У - тезки, на множестве студентов Вашей группы. 2. Х r У Û Х и У ровесники, на множестве людей. 3. х r у Û х - у 4. х r у Û х - у Î Z на R. 5. х r у Û х || у, на множестве прямых плоскости. 6. х r у Û последняя цифра числа х совпадает с последней цифрой числа у, на N. 7. х r у Û х и у числа одного знака на Z°. 8. х r у Û х 9. (а, в) r (с, d)Û а + d = в +с на N х N. 10. (а, в) r (с, d) Û аd = вс, на Z° х Z°. 11. х r у Û Sin х = Sin у, на R. 12. х r у Û ху > 0 или х 11. 4. Докажите, что a - отношение эквивалентности на R и найдите класс смежности элементов а и в.
2. х a у Û || х - 1| -3 | = || у- 1| -3 |, а = -2, в = 2. 3. х a у Û |х 4. х a у Û | (х - 1) 5. х a у Û Sin 6. х a у Û Sin 7. х a у Û Sin
8. х a у Û |2IхI 9. х a у Û |2 IхI- 4| = |2IуI- 4 |, а = 2, в = 1. 11.5. Найдите минимальное отношение эквивалентности r на множестве А = {1, 2, 3, 4, 5,} так, чтобы: 1. 1 r 2 и 2 r 3. 2. a = 3. a = 11.6. Пусть a и b - отношение эквивалентности на А. Докажите: 1. a 2. a о b - отношение эквивалентности Û a и b перестановки. 3. 11.7. Заданы отношения эквивалентности a и b. Найдите a Ç b, a 1. а a в Û а º в (mod 4), а b в Û а º в (mod 6). 2. а a в Û а º в (mod 5), а b в Û а º в (mod 3). 11. 8. Сколько различных отношений эквивалентностей можно задать на множестве: 1. из двух элементов; 2. из трех элементов; 3. из четырех элементов?
З А Н Я Т И Е № 12.
Отношение порядка. Теоретические вопросы: Определение нестрогого порядка, строгого порядка, линейного порядка. Понятие наибольшего, наименьшего, максимального, минимального элемента. Число линейных порядков n - множества. Упр 1. Выясните, является ли r отношением порядка на А. Определите тип порядка. Найдите экстремальные элементы 1. r = {(1, 2), (3, 2), (1, 3)}, А = {1, 2, 3} 2. r = {(х, у), у = х + 2}, А = R. 3. r = {(4, 2), (2, 3), (4, 3)}, А = {2, 3, 4, 5}. 4. r = {(х, у), х 5. r = {(х, у), х 6. х r у Û х делит у Ú х < у, А = |N. 7. (а, в) r (с, d) Û а < с Ú (а = с Ù в £ d), А = Z х Z. Упр 2. Найдите экстремальные элементы на множестве А относительно r. 1. х r у Û х делит у, А = N, 2. х r у Û х делится на у, А = N 3. х r у Û х делит у. А = N 4. х r у Û х делит на у. А = N È {0}. 5. х r у Û х делит у. А = N {1}. 6. Х 7. х r у Û х < у, А = [0, ¥). 8. х r у Û х делится на у, А =Д Д Упр 3. r - отношение порядка на А. Изобразите r диаграммой. Найдите экстремальные элементы. 1. х r у Û х делит у, А = Д 2. х r у Û х делится на у А = Д 3. х r у Û х делится у. А = Д 4. х r у Û х делит у, А = Д Упр 4. 1. Пусть: r - строгий (нестрогий) порядок. Каким будет r?. 2. Если r - строгий порядок, то r È порядок. 3. Если r - нестрогий порядок, то r È порядок. 4. Если r отношения порядка то r порядка. 5. Если a, b - отношения строгого порядка. Каким будет a Ç b?.
З А Н Я Т И Е № 13.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.31 (0.008 с.) |

 в Ù (а ³ в Ú а + в-
в Ù (а ³ в Ú а + в- .Найдите a о b, b о a, a
.Найдите a о b, b о a, a  , a È
, a È  ,a Ç b, a
,a Ç b, a 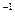 , если
, если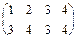 , b=
, b= 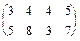 , n =
, n =  , 2. a = {(х,у), у =
, 2. a = {(х,у), у = 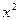 - 2х + 3}, b =
- 2х + 3}, b =  ,n = {(х, у), у= 2х - 1}
,n = {(х, у), у= 2х - 1} , n =
, n = 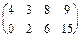 .
. = {(а, а), а Î А}
= {(а, а), а Î А} ,
, для отношения r, если:
для отношения r, если: у = х
у = х 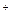 а = 100
а = 100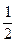
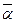 , a Ç b, a Èb, a \ b - симметричны.
, a Ç b, a Èb, a \ b - симметричны.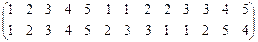
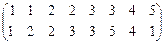


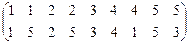
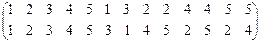
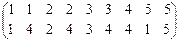
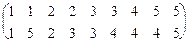
 1. х a у Û || х | -2| = || у | -2 |, а = 2, в = 1.
1. х a у Û || х | -2| = || у | -2 |, а = 2, в = 1.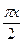 = Sin
= Sin 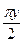 , а =1, в = 2.
, а =1, в = 2. = Sin
= Sin 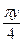 , а = 1, в = 2.
, а = 1, в = 2. - 2| = |2IуI- 2|, а = 2, в = 1.
- 2| = |2IуI- 2|, а = 2, в = 1.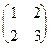 Ì r.
Ì r.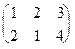 Ì r 4. 5 r 1.
Ì r 4. 5 r 1. = N \ {1}.
= N \ {1}. У Û Х Ì У, Х,У Ì Р (М).
У Û Х Ì У, Х,У Ì Р (М). .
.



