
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство от противногоСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Метод доказательства от противного основан на замене доказательства теоремы А ® В доказательством равносильной ей: а) А ® В «А Ù б) А ® В «А Ù в) А ® В «А Ù В каждом из трех случаев рассуждение идет по следующей схеме: предполагается истинность условия и отрицания заключения теоремы, а затем доказывается, в первом случае, два противоречащих друг другу предложения С и П р и м е р 3. Во всяком треугольнике против равных углов лежат равные стороны. ДОКАЗАТЕЛЬСТВО. Эта терема является обратной по отношению к теореме: во всяком треугольнике против равных сторон лежат равные углы. Пусть в треугольнике АВС ÐА = ÐС, докажем, что ВА = ВС. Предположим противное, т.е. что ВА ¹ ВС. Тогда одна из сторон должна быть больше другой, и, следовательно, согласно прямой теореме, один из углов А или С должен быть больше другого. Это противоречит условию, что ÐА = ÐС; значит, нельзя допустить, что стороны АВ и ВС не равны, поэтому АВ = ВС. (Второй случай).
Теоретические вопросы: Отношение следования и равносильности. Определение математических понятий. Теоремы. Взаимно обратные и противоположные теоремы. Необходимые и достаточные условия. Доказательство от противного.
6.1. Даны два предиката на R. Установите между ними отношение логического следования: 1. x > 1 и х > 2; 2. x ³ 3 и x ³ 5; 3. x < 4 и x < - 1; 4. x £ 3 и x £ 0; 5. (x - 1) (x + 2)=0 и (x - 1 = 0) Ù (x + 2 = 0); 6. x 7. x 8. х 9. | x | < 2 и x < 2; 10. | x | > 3 и x > 3; 11. | x - 1 | £ 2 и x £ 3; 12. | x + 2 | ³ 1 и x £ -3; 13. x > 2 и 15. 6.2. Даны два предиката на некотором универсальном множестве U. Установите между ними отношение логического следования. 1. x Î А и x Î А \ В; 2. x Î А и x Î А Ç В; 3. x Î А и x Î А È В; 4. x Î А Ç В и x ÎА \ В. 6.3. Равносильны ли на множестве R следующие предикаты? 1. x = 0 и x (x 3. x + 1 =0 и (x + 1) 5. 7(x - 3) = 49 и х - 3 = 7; 6. x+5=x-1 и x(x-3)=x 7. 9. х + 3 > 2 и х + 10. 2x - 1 < 5 и 2x 11. sin x + cos x = 1 и (sin x + cos x) 12. 13. 14. 15. log 16. lg (x + 1) = lg (2x + 3) и x + 1 = 2x + 3; 17. arcsin x = 1 и x = sin 1; 18. arcsin x = 3 и x = sin 3; 19. x 20. x 21. 22. 6.4. Запишите на языке предикатов определения: 1. - делимости целого числа n на целое число m; 2. - коллинеарности векторов а и в; 3. - ограниченной функции из R в R; 4. - периодической функции; 5. - наибольшего элемента на М относительно <.
6.5. Укажите род и видовое отличие в определениях четырехугольника, прямоугольника, ромба, квадрата, равнобедренного треугольника, равностороннего треугольника, трапеции. 6.6. Укажите ошибки в следующих определениях: 1. прямоугольник - это, когда все углы прямые; 2. отрезок - это прямая, ограниченная с двух сторон; 3. луч - это прямая, ограниченная с одной стороны; 4. простое число - это, когда оно имеет два делителя; 5. углом, вписанным в окружность, называется угол, образованный двумя хордами; 6. окружностью называется фигура, состоящая из всех точек, равноудаленных от данной. 6.7. Выделите условие и заключение в следующих теоремах и сформулируйте их в виде: “ Если..., то...”: 1. перпендикуляр к одной из двух параллелных прямых есть также перпендикуляр к другой; 2. вертикальные углы равны; 3. сумма углов треугольника равна 180 4. диагонали ромба взаимно перпендикулярны; 5. сумма двух смежных углов равна 180 6. против равных сторон треугольника лежат равные углы; 7. дуги, заключенные между равными хордами, равны; 8. диагонали параллелограмма делятся в точке пересечения пополам.
6.8. Для каждого из следующих утверждений сформулируйте обратное к нему, противоположное и противоположное к обратному утверждению. Укажите, истинно оно или ложно, дайте обоснование: 1. квадратное уравнение имеет корни только в том случае, когда его дискриминант неотрицателен; 2. если дискриминант квадратного трехчлена равен нулю, то его корни совпадают; 3. сумма корней квадратного трехчлена х равна - p, а произведение корней равно q; 4. квадратный трехчлен с неотрицательным дискриминантом можно разложить в произведение линейных множителей.
6.9. Вместо многоточия вставьте одно из выражений “ необходимо, но не достаточно”, “ достаточно, но не необходимо “, “ необходимо и достаточно” - так, чтобы получилось истинное высказывание: 1. а - четное число... для того, чтобы 3а было четным числом; 2. а делилось на с... для того,чтобы а,в делилось на с; (а, в, с Î Z); 3. а и в делятся на с... для того, чтобы а + в дели- лось на с (а, в, с Î Z); 4. делимость числа на 4... для того, чтобы оно дели- лось на 8; 5. свойства треугольника быть равносторонним... для того, чтобы он был остроугольным; 6. x Î A... x Î A È B; 7. x Î A... x Î A Ç B; 8. x Î A... x Î A \ B; 9. x Î A È B... x Î A Ç B; 10. x Î A È B... x Î A \ B; 11. x Î A Ç B... x Î A \ B; 12. ав = 0... для того, чтобы а = 0 и в = 0; 13. а < 2 и в < 5... для того, чтобы а + в < 7.
6.10. Для каждого из следующих утверждений о натуральных числах дайте три разные формулировки, используя слова: “ достаточно”, “ необходимо”, “ только тогда, когда”: 1. если а делится на 24, то а делится на 2 и на 3; 2. если а делится на 20 и на 30, то а делится на 60; 3. если произведение двух чисел делится на простое число р, то хотя бы один из сомножителей делится на число р; 4. если а делится на два различных простых числа, то а делится на их произведение; 5. если число имеет ровно два различных делителя, то оно простое. 6.11. Сформулируйте каждое из следующих утверждений о натуральных числах при помощи слов; “если..., то...”; 1. для того чтобы число делилось на 12, достаточно, чтобы оно делилось на 6 и на 4. 2. а 3. для того, чтобы а чтобы а делилось на 10 и на 6; 4. для того, чтобы а делилось на в, необходимо, чтобы а делилось на любой простой делитель в; 5. число имеет не более двух различных делителей только тогда, когда оно простое или равно 1. 6. для того, чтобы а делилось на произведение bc, необходимо, чтобы а делилось на b и на с. 6.12. Руководствуясь определением импликации, сформулируйте: 1. достаточное, но не необходимо условие ложности импликации; 2. необходимое, но недостаточное условие ложности импликации; 3. необходимое и достаточное условие ложности им- пликации; 4. необходимое и достаточное условие истинности импликации 6.13. Методом от противного докажите следующие теоремы: 1. в круге равные хорды одинаково удалены от центра и стягивают равные дуги; 2. в круге хорды, одинаково удаленные от центра, равны и стягивают равные дуги; 3. если одно из слагаемых делится на 7, а другое - нет, то сумма не делится на 7; 4. две прямые, параллельные третьей, параллельны; 5. если две параллельные прямые пересечены какой-нибудь прямой, то соответственные углы равны; 6. бесконечность множества простых натуральны чисел; 7.доказать, что число
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.187 (0.007 с.) |

 В ® С Ù
В ® С Ù 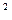 + 6 +
+ 6 +  = 5x +
= 5x + 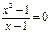 ;
; ; 14. x < 2 и
; 14. x < 2 и 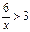 ;
; > 0 и 3 < x < 5; 16. 2 < x < 3 и
> 0 и 3 < x < 5; 16. 2 < x < 3 и  >1.
>1. 
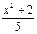 =
=  ;
;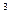 =0; 4. 2x = 10 и (2х-10)(х+1)=0;
=0; 4. 2x = 10 и (2х-10)(х+1)=0;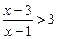 и х - 3 >3(x - 1); 8. 2x>1 и 2х + х
и х - 3 >3(x - 1); 8. 2x>1 и 2х + х 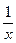 + 3 > 2 +
+ 3 > 2 +  = 1 и x
= 1 и x 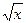 =
=  и x = 2x + 1;
и x = 2x + 1; =
=  и 1- x = 2x;
и 1- x = 2x; (x+2) = log
(x+2) = log  > x
> x  > x + 1 и x > (x + 1)
> x + 1 и x > (x + 1)  ;
; не является рациональным.
не является рациональным. З А Н Я Т И Е № 7.
З А Н Я Т И Е № 7.


