
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Высказывания и операции над нимиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Определение. Предложение, относительно которого можно сказать истинно оно или ложно, называют высказыванием. Например, следующие предложения являются высказываниями: а) 6 кратно 3; б) число 1 является решением уравнения х - 1 = 0; в) 1 есть простое число; г) 5 > 3; д) 2.2 = 5; е) 5 есть чётное число; ж) город Кызыл - столица Тувы. Предложения а), б), г), ж) - истинные высказывания; предложения в), д), е) - ложные. Вопросительные и восклицательные предложения высказываниями не являются. Определения высказываниями также не являются, так как представляют собой условное соглашение о введении нового термина. Под значением высказывания будем понимать его истинностное значение (“истина” или “ложь”). Обозначаем высказывания: А, В, С и т.д., а их значения “истина” или “ложь” соответственно буквами И и Л. В логике высказываний нас интересуют связи, которые определяются тем, каким образом одни высказывания строятся из других, называемых элементарными. В предложениях: а) “если 10 делится на 3, то 100 делится на 3”; б) “10 делится на 3 и 100 делится на 3”; в) “10 делится на 3 или 100 делится на 3”; г) “неверно, что 10 делится на 3”, - можно выделить элементарные высказывания А: ”10 делится на 3” и В: “100 делится на 3”. Структура этих предложений: “если А, то В”, “А и В”, “А или В”, “неверно, что А”. Союзам “и”, “или”, “если, то”, “неверно, что” в логике высказываний соответствуют логические операции конъюнкции, дизъюнкции, импликации, отрицания. Определение. Отрицанием высказывания А называется новое высказывание “неверно, что А” (обозначение “ Значение отрицания полностью определяется истинностной таблицей:
Чтобы построить отрицание элементарного высказывания, достаточно поставить слова “неверно, что” перед данным высказыванием, либо перед сказуемым поставить частицу “не”. ПРИМЕРЫ. А: “Сегодня я сдаю экзамен”.
В: 2 Î Z; Определение. Конъюнкцией двух высказываний А и В называется новое высказывание “А и В” (обозначение “АÙВ”), которое истинно тогда и только тогда, когда оба высказывания истинны. Определение. Дизъюнкцией двух высказываний А и В называется новое высказывание “А или В”, (обозначение “АÚВ”), которое истинно тогда и только тогда, когда истинно хотя бы одно из этих высказываний. Определение. Импликацией двух высказываний А и В называется новое высказывание ”если А, то В” (обозначение “А®В”), которое ложно только в том случае, когда А истинно, а В ложно. Определение. Эквиваленцией двух высказываний А и В называется высказывание “А тогда и только тогда, когда В” (обозначение “А«В”),которое истинно в том и только в том случае, когда А и В оба истинны или оба ложны. Значения истинности результатов вышеприведённых логических операций задаются истинностной таблицей:
С помощью логических операций над высказываниями можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками, ((х Ù у) v ┐z). Определение (формулы, индуктивное): 1. Всякая переменная: х, у, z… взятая в отдельности есть формула, символы 0, 1 – также формулы. 2. Если А, В – формулы, то следующие выражения суть формулы: (АÙВ), (А v В), (А→В), ┐А. 3. Никакие другие выражения, составленные из переменных и символов логических операций, не являются формулой. Обозначаем формулы буквами А, В, С. Пример: х, у, (х Ù у), ((х Ù у) → у) – формулы. (х Ù у) →, х Ù у – формулами не являются. В определении формулы четко вырисована структура: у любой формулы есть главный логический знак, тот, который фигурирует последним. Скобки играют большую роль, но и делают записи громоздкими. Мы договоримся о сокращении числа написания скобок. Внешние скобки опустим. Договоримся о приоритете логических символов, т.е. об их силе связывания. Порядок таков: ┐, И вместо ((х Ù у) → х) пишем ху → х
Определение (Подформулы, индуктивное): 1.Подформулой формулы пункта 1 является она сама. 2. Подформулами формулы пункта 2 являются: А, В, она сама, все подформулы формулы А и все подформулы формулы В.
Контрольные вопросы и устные упражнения 1. Понятие высказывания. Являются ли следующие предложения высказываниями и найдите истинностные значения, если это возможно: 1. 6 кратко 3; 2. функции у = х2 монотонно возрастает; 3. 5 > 3; 4. 2 × 2 = 5; 5. натуральное число делится на 3; 6. если натуральное число х ³ 3 то х > 7. 2. Определение операции отрицания. Каковы значения Р и Q, если Ø Р - л, ØØ Q - и? 3. Определение операции дизъюнкции. Каковы значения высказываний Р и Q, если Р Ú Ø Q - л? 4. Определение операции конъюнкции. Каковы значения высказываний Р и Q, если Ø Р Ù Q - и? 5. Определение операции импликации. Найдите значение R, если Ø Q и ( 6. Определение операции эквиваленции. 7. Понятие формулы. Тождественно истинная и тождественно ложная формулы. Порядок выполнения логических операций. Таблица истинности.
Упражнения 3.1. Выясните логическую структуру следующих предложений: 1. число 9 является рациональными или иррациональными; 2. если углы вертикальные, то они равны; 3. треугольник АВС равнобедренный или прямоугольный; 4. число 56 не делится на 9; 5. если число целое и положительное, то оно натуральное.
3.2. Сформулируйте отрицание следующих высказываний: 1. 257 - четное число; 2. число 3. число 23 делится на 7; 4. число 9 положительно; 5. 3 > 5: 6. 5 + 3 = 8; 7. 30 - простое число; 8. Луна больше Земли; 9. Аня старше Тани; 10. 2 ³ 10. Укажите, что является истинным: само высказывание или его отрицание.
3.3. Для каждого из следующих высказывании составьте отрицание, а затем двойное отрицание. Убедитесь, что двойное отрицание совпадает по смыслу с исходным высказыванием. 1. 15 делится на 3; 2. 5 - положительное число; 3. 3 < 7; 4. - 3 £ 3. 3.4. Являются ли следующие высказывания отрицанием друг друга. 1. “число 47 простое” и “число 47 составное”; 2. “угол
3.5. Определите значения истинности высказываний. 1. число 321 делится на 3 и на 9; 2. число 321 делится на 3 или на 9; 3. 2 - нечетное число ® 2 Ø 3; 4. (2 Ø 3) \/ (2 <3) ® (2 < 5); 5. Ø (5 - простое число) /\ (2 < 5) ® (2 < 5); 6. Ø (2 < 3) ® (2 < 3 ® 2 < 4); 7. (2 = 3) ® (4 = 2 × 3); 8. (3 < 4) ® (6 ³ 5); 9. Ø (5 < 3) /\ (3 £ 2) ® (3 <5); 10. ((7: 2 = 3) \/ 2 - простое число) /\ Ø (2 £ 3). 3.6. Известно, что высказывание А истинно. Можно ли, зная лишь это, определить значение истинности высказывания вида: А /\ В; А \/ В, А ® В; А «В; Ø А?
3.7. Даны числа: 31, 53, 409, 348, 20, 3094, 233, 33, 271, 143, 3, 333, 14, 30. Выпишите все числа, в записи которых: 1. три цифры и есть цифра 3; 2. три цифры или есть цифра 3; 3. есть цифра 3 и число делится на 2; 4. есть цифра 3 или число делится на 2.
3.8. Найдите логические значения формул при заданных значениях высказываний: 1. Ø(А Ú Ø В) А ®, если А - и, В - Ù; 2. (Ø А ® Ø С) Ú (В ® А), если А - Ù, В - и, С - и; 3. (Ø А Ú С) Ù (С ® В), если А - Ù, В – и; 4. Ø ((В ® А) Ú (А ® Ø В), если А - Ù; 5. (В ®(Ø В ®(С Ú А))) ®В, если В – и; 6. (Ø А ® Ø С) Ú (В ® А), если А - Ù, В - и, С - и; 7. Ø (С Ú В) ®(А Ú Ø Д), если (ØА Ù В)®(С Ú Ø Д) - Ù.
3. 9. Укажите порядок действий, определите название предложения: 1. А ® В ® Ø С Ù (Ø Д Ú Е); 2 Ø А® В Ù С Ú А; 3. (А® Ø В) Ù Ø А Ú С; 4. Ø(А Ú В Ù Ø С).
3.10. Расставьте скобки в предложениях так, чтобы получить разные формулы. Сколько их получится? 1. А Ù Ø В ® С; 2. Ø А Ú В Ù С ® Ø В; 3. Ú Ø В ® А «Ù А Ù В; 4. А Ú Ø В ® А Ú С; 5. А Ú Ø В Ù Ø С Ú С; 6. А Ù С ® Ø А Ú В «А.
3. 11. Построить таблицы истинности формул. Является ли формула тождественно истинной (ложной)? 1. А ® А; 2. А Ú Ø А; 3. А Ù Ø А; 4. Ø(А «В); 5. А Ú В ® А; 6. А ® А Ú В; 7. А Ù В ® А; 8. А ® А Ù В; 9. А ® А Ù Ø В; 10. А Ú В ® А Ù В; 11. А Ù Ø В ® Ø А Ù В; 12. Ø(А Ù В ® А); 13. Ø(А Ù С ® Ø В Ú А); 14. Ø(А ® В) Ú (В ® С); 15. (А Ù Ø В Ù Ø В Ù Ø С).
3.12. Методом от противного докажите тождественную истинность формул: 1. (А ® В) Ù А ® В; 2.(А ® В) ®(А Ù С ® В); 3. (А ® В) ®(А Ù С ® В).
З А Н Я Т И Е № 4. Равносильные преобразования формул алгебры логики. Пусть дана формула А = ┐(х v у) → х┐у. Здесь переменные принимают значения из множества {0,1}. В зависимости от значений х, у определенное значение принимает формула А.
х у х v у ┐(х v у) ┐ у х┐у ┐(х v у) → х┐у 1 1 1 0 0 0 1 1 0 1 0 1 1 1 0 1 1 0 0 0 1 0 0 0 1 1 0 0
Можно сократить работу по нахождению истинного значения формулы. Всякая формула есть функция с областью определения {0, 1} и областью значений {0,1}. Пусть х1, х2, …, хn – список переменных, если эта последовательность содержит все переменные, входящие в формулу А. Придавая значения α1 ,α2 , …, αn всем переменным, а их 2n (почему?), мы вычислим соответствующие значения формулы А. Фактически формула А является суперпозицией функций v, →, ┐ У нас есть эффективный способ вычисления значения формулы в двоичном наборе – алгоритм вычисления истинности всякой формулы. Введем понятие равносильных формул. Определение. Даны две формулы А и В алгебры логики и х1, х2, …,хn – список переменных, входящих в формулы А и В. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на каждом наборе значений переменных и записываются: А ≡ В или А = В. Пример: х → у = ┐х v у, х v ┐х ≠ (х v ┐х)у, у = (х v ┐х) у Формулы различны, функции одинаковы. Определение. Формула А называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных. Определение. Формула А называется тождественно ложной (противоречие), если она принимает значение 0 при всех значениях входящих в нее переменных. Очевидно, что отношение равносильности рефлексивно, симметрично и транзитивно. Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А↔В– тавтология, и обратно, если формула А↔В – тавтология, то А и В равносильны. Основные равносильности: 1. ху = ух 2. х v у = у v х 3. х(уz) = (ху)z 4. х v (у v z) = (х v у) v z 5. (х v у)z = (хz) v (уz) 6. ху v z = (xz) v (yz) 7. ┐ху = ┐х v ┐у 8. ┐(x v y) = ┐x Λ ┐y 9. х → у = ┐х v у 10. x v y = ┐х → у 11. х → у = ┐у → ┐х 12. ┐┐x = x – закон снятия двойного отрицания 13. 14. х v х = х идемпотентности 15. х Ù 0 = 0 16. х Ù 1 = х 17. х v 1= 1 18. х v 0 = х 19. х v ┐х = 1 20.х Ù ┐х = 0 – закон противоречия. Выделим ряд равносильностей, которые встречаются часто и позволяют значительно упростить формулу. Здесь символами А, В обозначаются произвольные формулы Правила сокращения: 1. Ах v А┐х = А – склеивание 2. Ах v ┐х = А v ┐х – удаление Ах v ┐х = А v ┐х – удаление А┐х v х = А v х – удаление 3. А v АВ = А – поглощение А(А v В) = A – поглощение Данные правила предлагается доказать самостоятельно Определение. Операция подстановки Тогда, если А = В, то Упростить: 1. (┐(х v y) → x v y)y = (x v y v x v y)y = (x v y)y = xy v y = = (x v 1)y = y 2. (x → y) → ((y → z) →(x v y → z)) = ┐(┐x v y) v (┐(┐y v z) v v (┐(x v y) v z)) = x┐y v y┐z v ┐x┐y v z = ┐y(x v ┐x) v v (y v z)(┐z v z) = ┐y v y v z = 1 Контрольные вопросы и устные упражнения 1. Понятие равносильных формул. Основные равносильности. Равносильны ли: 1). А и Ø Ø А; 2). А ® В и В Ú Ø А; 3). А Ù В и Ø (А Ù В) Ú (А Ù С)? 2. Законы логики. Докажите законы дистрибутивности, де Моргана, идемпотентности, контрапозиции. 3. Принцип двойственности в алгебре логики. 4. Какая связь между алгеброй логики и алгеброй множеств? Упражнения
4. 1. Являются ли законами логики следующие формулы: 1. х ® х Ú у; 2. х Ù у ® х Ú у; 3. х Ú (х ® у); 4. х Ú у ® х Ù у?
4.2. Равносильны ли формулы: 1. х Ù у и х Ú у 2. х ® у и х Ú у 3. х Ú (Ø х Ù у) и х Ú у 4. х ® у и Ø у® Ø х 5. (х ® у) Ù (Ø х ® Ø у) и (у ® Ø х) ®(Ø х Ù Ø у)
4.3. Упростите, используя равносильные формулы: 1. х Ú (х Ú у); 2. у Ù (х Ù у); 3. Ø х Ú (х Ú у); 4. (х Ù у) Ù Ø х; 5. х ® х; 6. х ® (х ® у); 7. х ® (х ® Ø х); 8. х ® Ø х Ú Ø у; 9. Ø х Ù у ® х Ú у; 10. (х ® у) Ú (х Ù Ø у); 11. Ø (Ø х Ú у) ®((х Ú у) ® х; 12. Ø (Ø хØ у) Ú ((х ® у) Ù х); 13. (х ® у) Ù (у ® х) Ù (х Ú у); 14. (у ® х) Ù у ® Ø х) Ù (z ® х); 15. (х Ù z) Ú (х Ù Ø z) Ú (у Ù z) Ú (Ø х Ù у Ù z); 16. Ø((х ® у) Ù у ® Ø х)); 17. Ø (Ø х Ú (у ®(z® х Ù у Ú Ø z))).
4.4. Проверить равносильность формул: 1. х Ú (Ø х Ù у) и х Ú у; 2. х ® у и Ø у ® x; 3. (х ® у) Ù (Ø х ® Ø у) и (у ® Ø х) ®(Ø х Ù Øу); 4. х ® (у Ú (z ® Ø х)) и х Ù z ® у.
4.5. Докажите следующие теоремы: 1. если А, то А Ú В; 2. если А Ù В, то В; 3. если (ØА Ú В) Ù (С ® Ø В), то (А ® Ø С).
4.6. Равносильным образом следующие формулы преобразуйте так, чтобы они содержали только операции Ø и Ù. 1. (х È у) ® (Ø х ® z); 2. (Ø х ® у) Ú Ø (х ® у); 3. ((х Ú у Ú z) Ú х) Ú z; 4. ((х ® у) ® z) ® Ø х.
4.7. Равносильным образом следующие формулы преобразуйте так, чтобы они содержали только операции Ø и Ú. 1. (х ® у) ®(у Ù z); 2.(Ø х Ù у) ® (х Ù у); 3. ((Ø х Ù Ø у) Ú z) Ùz Ù Ø у); 4. ((х®(у Ù z) ®(Øу ® Ø х)) ® Øу.
4.8. Равносильными преобразованиями формул освободитесь от знаков “®“ и “«“, отрицание отнести к переменным: 1. Ø х ® Ø у; 2. х «х Ú у; 3. х ® у Ú Ø х; 4. х ® х «Ø у; 5. ((х ® у) Ù (у ® х)) ® (х Ú у); 6. ((х ® у) Ù (у ® Ø х)) ®(z ® х); 7. Ø (х ® у); 8. Ø (х ® (у ® х)); 9. Ø (Ø(х Ú у) ®(z ® х)); 10. Ø((х Ù (у Ú Ø z)) Ú (Ø х Ù у)).
4.9. Двумя способами докажите тождественную ложность формул. 1. Ø (х ® х Ú у); 2. Ø (х Ú у ® х Ú у); 3. х Ú у «х Ù Ø у; 4. ®(х ®у)); 5. ((х ®у) Ù (у ®z)) Ù Ø (х®z); 6. (х ®у) Ù (х® Ø у) Ù х.
З А Н Я Т И Е № 5.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

 А”), которое получается из А добавлением к нему слова “неверно, что...” и которое истинно тогда и только тогда, когда А ложно.
А”), которое получается из А добавлением к нему слова “неверно, что...” и которое истинно тогда и только тогда, когда А ложно. или v, →,
или v, →,  .
.
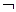 Р Ú Р) Ù (Q ® R) ложные высказывания.
Р Ú Р) Ù (Q ® R) ложные высказывания. рациональное;
рациональное; хх = х – закон
хх = х – закон – результат замены каждого вхождения переменной х формулой С.
– результат замены каждого вхождения переменной х формулой С.



