
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторов. Базис и ранг системы векторов.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теоретические вопросы; 1. Определение линейно зависимой, линейно независи- мой системы векторов. 2. Что означает линейная зависимость в случае, когда сис- тема состоит из одного вектора? Из двух векторов? 3. Какая система векторов называется ступенчатой? Из не- скольких векторов может состоять ступенчатая система? Почему? Ступенчатая система векторов линейна независима? 4. Определение базиса конечной системы векторов. 5. Ранг конечной системы векторов (определение). 6. Из скольких векторов может состоять базис системы векторов в. 7. На сколько единиц ранг основной матрицы может отли- чаться от ранга расширенной матрицы? Упр № 1. а) Докажите, что если подсистема системы век- торов линейно зависима, то система линейно зависима. б) Сформулируйте обратную противоположной теореме для г). в) Если упороченная система векторов линейно независима, то удлиненная линейно независима. г) Докажите, что если строки основной матрицы линейно независимы, то система уравнений совместна при любом столбце свободных членов. Сформулируйте и докажите обратное утверждение. Домашнее задание: Докажите, что система содержа - шая а) нулевой вектор линейно зависима. б) два коллинеарных вектора линейно зависимы в) два равных вектора линейно зависима. Почему условия а, б, в только достаточны для линей- но независимости?
Упр № 2. Выясните, являются ли следующие системы векторов линейно зависимыми или линейно независимыми. а) б)
в)
Упр № 3. Выясните, при каких значениях параметра а век- торы каких значениях оин будут линейно независимы, если
Упр № 4. Найдите все значения линейно выражается через векторы
а) б)
Упр № 5. Пусть система вектор сима. Докажите, что системы а) б) Упр № 6. Найдите базис и ранг системы векторов и осталь- ные векторы выразите через этот базис: а)
б)
Упр № 7. Найдите все базисы системы векторов: а) б)
Домашнее задание: 1. Исследуйте на линейную зависимость систему векторов:
2.. Найдите какой нибудь базис ситемы векторов и выра- зите остальные векторы через этот базис.
3. Найдите все базисы системы векторов:
4. Выражается ли вектор
5. Докажите, что векторы базис R4, Найдите координаты вектора базисе:
З А Н Я Т И Е № 15.
Критерий совместности системы линейных Уравнений. Теоретические вопросы; 1. Определение ранга матрицы. 2. Критерий совместности системы линейных уравнений 3. Критерий определенности системы линейных уравне- ний, критерий неопределенности. 4. Почему однородная система линейных уравнений всегда совместна. 15.1. Чему равен ранг матрицы при различных значениях l?
а) А = 15.2. Исследовать совместность и найти общее решение и одно частное решение ситемы уравнений. 1. 2х1 + 2х2 + 4х3 - х4 + 3х5 = 2 х1 +х2 +3х3 - 2х4 +3х5 = 1 3х1 +3х2 + 5х3 - 2х4 +3х5 = 1 2х1 + 2х2 +8х3 - 3х4 +9х5 = 2
2. 2х1 - х2 + х3 + 2х4 + 3х5 = 2 6х1 - 3х2 +2х3 + 4х4 +5х5 = 3 6х1 - 3х2 + 4х3 + 8х4 +13х5 = 9 4х1 - 2х2 +х3 + х4 +2х5 = 1
3. 2х1 + 5х2 - 8х3 = 8 4х1 + 3х2 - 9х3 = 9 2х1 + 3х2 - 5х3 = 7 х1 + 8х2 - 7х3 = 12
4. х1 + 2х2 + 3х3 - 2х4 + х5 = 4 3х1 + 6х2 +5х3 - 4х4 +3х5 = 3 х1 + 2х2 + 7х3 - 4х4 +х5 = 11 2х1 + 4х2 +2х3 - 3х4 +3х5 = 6
15.3. Найдите общее решение для систем уравнений. 1. х1 + х2 + х3 + х4 + х5 = 0
2.. х1 + 2х2 + 4х3 - 3х4 = 0 3х1 + 5х2 +6х3 - 4х4 = 0 4х1 + 5х2 - 2х3 + 3х4 = 0 3х1 + 8х2 +24х3 - 19х4 = 0
3. 3х1 + 5х2 + 2х3 = 0 4х1 + 7х2 + 5х3 = 0 х1 + х2 - 4х3 = 0 2х1 + 9х2 + 6х3 = 0
4. 5х1 + 6х2 - 2х3 + 7х4 + 4х5 = 0 2х1 + 3х2 -х3 + 4х4 +2х5 = 0 7х1 + 9х2 - 3х3 + 5х4 +6х5 = 0 5х1 + 9х2 - 3х3 + х4 +6х5 = 0
15.5. Исследуйте систему и найдите общее решение в зависимости от значения параметра l.
а) 5х1 - 3х2 + 2х3 + 4х4 = 3 4х1 - 2х2 +3х3 + 7х4 = 1 8х1 - 6х2 - х3 - 5х4 = 9 7х1 - 3х2 +7х3 + 17х4 = l
б) 2х1 + 3х2 + х3 + 2х4 = 3 4х1 + 6х2 +3х3 + 4х4 = 5 6х1 + 9х2 + 5х3 + 6х4 = 7
8х1 + 12х2 +7х3 + lх4 =9
Домашнее задание 1. Даны системы линейных уравнений:
а) 2х1 + х2 - х3 + 3х4 = 0 3х1 - х2 - х3 + х4 = 0 х1 + 3х2 - х3 + 5х4 = 0
б) х1 + 21х2 + (1 - i) х3 = 0 -х1 + 2х2 + (-1 - i) х3 = 0 3х1 + 61х2 + (3 - 3i)х3 = 0 Докажите, что системы имеют ненулевые решения. Найдите общее решение и одно четное.
2. Даны системы линейных уравнений: а) 2х1 - х2 + 3х3 + 4х4 = 5 4х1 - 2х2 + 5х3 + 6х4 =7
б) х1 + х2 + 3х4 = 5 4х1 + х2 + 2х3 - х4 = 6 3х1 - 4х3 - х4 = -2 2х1 - х2 +3х3 +6х4 =10
в) 3х1 - 5х2 + 2х3 + 4х4 = 2 7х1 - 4х2 + х3 + 3х4 = 5 5х1 + 7х2 - 4х3 - 6х4 = 3
Исследуйте совместность и найдите общее решение и одно частное решение систем уравнений.
3. Вычислите ранг матрицы в зависимости от параметра а.
Дополнительные задания: 1. lх1 + х2 + х3 = 1 х1 + lх2 + х3 = 1 х1 + х2 +lх3 = 1
2. (1 + l) х1 + х2 + х3 = 1 х1 + (1 + l)х2 + х3 = l х1 + х2 + (1 + l)х3 = l2
З А Н Я Т И Е № 16.
Определители
Теоретические вопросы:
1. Определитель квадратной матрицы порядка n (определение) 2. Запишите формулу для вычисления определителя 2-ого и 3-го порядка. 3. Основные свойства определителя. 4. Достаточные условия равенства нулю определителя 5. Миноры и их алгебраические дополнения. 6. Способы вычисления определителей. П р и м е р. 16.1. Вычислите определители: 1. 4. 16.2. Выясните, какие из приведенных ниже произведений входят в определители соответствующих порядков и с какими знаками: а) а43 а21 а35 а12 а54 б) а61 а23 а36 а12 а54 в) а27 а36 а51 а74 а25 а43 а62 16.3. Выберите значения i и k так, чтобы произведение а62 аi5 а33 ак4 а46 а21 входило в определитель 6 - го порядка со знаком минус. 16.4. а) Выпишите все слагаемые входящие в определитель 5 - го порядка и имеющие вид а14 а23 а3 L3 а4L4 а55 б) Выпишите все слагаемые входящие в определитель 4 - го порядка со знаком минус и содержащие множитель а23.
16.5. Вычислите определители 3 - го порядка. 1.
4. 16.6. Разложите определитель по элементам 3 - го столбца.
Упр 7. Вычислите определители методом приведения к треугольному виду: а) Упр 8. Вычислите определители:
1.
3.
5.
Упр 9. Дан определитель Д =
а) Запишите разложение определителя по второй строке. б) Составьте определитель Д1, заменив 3 - й столбец определителя Д линейной комбинацией 1 - го и 2 - го столбца с коэффициентами l1 = -1, l2 = 3 в) Вычислите определитель Д, получив предварительно нули в какой-либо строке или столбце. Верно ли, что Д1 = Д? г) Поменяйте местами 1-й и 2-й столбца определителя Д. Вычислите полученный определитель.
Дополнительные задания: 1. Докажите, что 2. Решите уравнения: а)
Домашнее задание 1. Вычислите определители: 1). 3). 2. Вычислите определители 3 - го порядка: 1. 3. С какими знаками входят данные произведения в определители соответствующих порядков: 1. а13 а22 а31 2. а12 а23 а34 а45 а56 а67 а78 а81? 4. Входят ли в определитель 5-го порядка произведения: 1. а13 а24 а23 а41 а55 2. а21 а13 а34 а55 а42?
Дополнительные задания: 1. Используя утверждения |А × В| = |А| × |В|, докажите: 1) Если матрица А - невырожденная, то |А-1| = |А|-1
2) Пусть матрица В - обратима. Докажите, что |В-1× А× В| = |А|
2. Решите относительно l уравнение | А - l Е| = 0, где 1). А =
З А Н Я Т И Е № 17.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.188.121 (0.018 с.) |

 1 = (1, 2, -1),
1 = (1, 2, -1),  1=(2, 1, -1, 1),
1=(2, 1, -1, 1),  1,
1,  , при которых вектор
, при которых вектор 
 линейно незави-
линейно незави- = (2, 1, 2) через векторы
= (2, 1, 2) через векторы б) А =
б) А = 

 2.
2.  3.
3. 
 5.
5. 
 2.
2.  3.
3. 
 5.
5. 

 б)
б)  2.
2. 
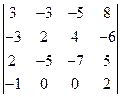 4.
4. 
 6.
6. 

 делится на 275.
делится на 275. = 0 б)
= 0 б)  = abc
= abc 2).
2). 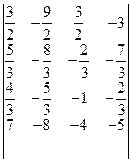
 4).
4). 
 2.
2. 
 2). А =
2). А = 



