
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запись решений уравнений, неравенств, системСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ТЫВИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Г.А. Троякова, О.П. Магеря АЛГЕБРА – 1 Практические занятия для студентов первого курса физико - математического факультета
Кызыл 2011 г. УДК 513
Г.А. Троякова., О.П.Магеря. Алгебра – 1.Практические занятия для студентов первого курса физико-математического факультета. ТывГУ.- Кызыл, 2009. – 56 с.
Настоящее пособие написано в соответствие с программой для специальности «математика», квалификация: «учитель математики». Оно представляет собой систему практических занятий по темам: элементы теории множеств и логики, бинарные отношения, системы линейных уравнений, - изучаемым в первом семестре.
Печатается по решению кафедры алгебры и геометрии, УМС физико-математического факультета ТывГУ.
Рецензенты: Доцент кафедры алгебры и математической логики Красноярского госуниверситета к.ф.-м.н. доцент кафедры высшей математики Красноярского политехнического Университета, к.ф.-м.н..
С Тывинский государственный университет
З А Н Я Т И Е № 1.
Множества Понятие множества В математике, да и в других науках, каждое новое понятие определяется обычно через уже известные, более элементарные понятия. Последнее, в свою очередь, определяется через ещё более простые и т.д., до тех пор, пока не придут к исходным понятиям. Понятие множества - исходное, первичное. Оно не поддаётся точному определению, его можно лишь описать, пояснить на примерах. Под множеством А будем понимать любое собрание определённых и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются элементами или членами множества А. Если элемент х принадлежит множеству А, то это обозначается так: х Î А, - если же х не принадлежит множеству А, то знак Î перечёркивают и пишут: х Ï А. Множество задано, если по отношению к любому объекту можно сказать, является он элементом этого множества или нет.
В алгебре чаще всего приходится иметь дело с числовыми множествами. Для некоторых из них приняты стандартные обозначения: N - множество натуральных чисел; Z - множество целых чисел; Q - множество рациональных чисел; R - множество действительных чисел. Например, запись -7 Î Z читают так: “число -7 является целым”, а запись -7 Ï N - “число -7 не является натуральным”. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Убедитесь в этом!
Обычно множество задаётся перечислением всех его элементов (если это возможно), например, М = {a, b, c}; выделением из более широкого указанием признака, характеристического свойства, по которому элементы данного множества отличаются от всех остальных, например, В = {x | x Î N и x < 7}. Задайте множество В перечислением! Определение. Множество называется конечным, если количество его элементов может быть выражено определённым (конечным) числом и обозначается: n(А). В противном случае множество называется бесконечным. Например, множество К всех двузначных чисел конечно и n(K) = 90, а множество натуральных чисел N бесконечно. Определение. Два множества А и В называют равными и пишут А = В, если А и В содержат одни и те же элементы. Например, множества С = {2, 3, 4, 5, 6} и L = {x | x Î N и х < 7} равны. Множества {1, 2, 3} и {3, 1, 2, 1} тоже равны, т.к. каждый элемент первого множества принадлежит второму множеству и наоборот; оба множества состоят из трёх элементов и, обычно, используют запись {1, 2, 3}.
Отношения между множествами Определение. Множество В называется подмножеством множества А (обозначение: В Ì А), если каждый элемент множества В является также элементом множества А. Пустое множество считают подмножеством любого множества ( Для наглядности множество изображается кругом (или другой связной фигурой) - круг Эйлера-Венна на плоскости мыслится как множество точек круга. Возможны следующие отношения между множествами А и В: а) множества А и В имеют общие элементы, но ни одно из них не является подмножеством другого (рис.1); б) множества А и В не имеют общих элементов (рис.2); в) одно из множеств, например В, является подмножеством другого (рис.3); г) множества равны (рис.4).
рис.1 рис.2 рис.3 рис.4
Определение. Пусть a, b Î R и a < b. Интервалом от a до b называется подмножество множества R, состоящее из всех тех чисел х. для которых a < x < b. Обозначение: (a; b).
a b x Аналогично даются определения:
б) открытый слева полуинтервал от a до b (обозначение: (a; b ]); определяющее неравенство: a < x £ b; изображение:
в) открытый справа полуинтервал от a до b. Указанные выше множества называют промежутками. Дайте полные определения для пунктов а), б), в)!
Операции над множествами Определение. Пересечением множеств А и В называется множество, состоящее из всех общих элементов этих множеств. Пересечение множеств А и В обозначается так: А Ç В. Определение можно записать в виде: А Ç В = { x | x Î A и х Î В } При помощи кругов Эйлера пересечение множеств А и В изображается заштрихованной областью:
рис.5 Заметим, что если множества А и В не имеют общих элементов, то А Ç В =
Определение. Объединением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А и В. Обозначение: А È В. Определение объединения можно записать в виде: А È В = { x | x Î A или х Î В } Заметим, что А È Объединение множеств А и В изображается с помощью кругов Эйлера заштрихованной областью:
рис.6 Определение. Разностью множеств А и В называется множество элементов, которые принадлежат множеству А и не принадлежат множеству В. Обозначение: А \ В. Определение разности множеств А и В можно записать в виде А \ В = { x | x Î A и х Ï В } Изображение:
рис.7
ПРИМЕР. Даны два множества: P = { x | x = 3k, k Î N, x <20 }, Q = { x | x = 4k, k Î N, x < 20 }. Найдите А È В, А Ç В, А \ В, В \ А. РЕШЕНИЕ. Зададим множества P и Q перечислением элементов: P = { 3, 6, 9, 12, 15, 18 }, Q = { 4, 8, 12, 16 }. Исходя из определений, имеем: P È Q = { 3, 4, 6, 8, 9, 12, 16, 18 }, P Ç Q = { 12 }, P \ Q = { 3, 6, 9, 15, 18 }, Q \ P = { 4, 8, 16 }. Определение. Универсальным называют такое множество, которое содержит в себе все множества, рассматриваемые в данной задаче. Обозначение: U или I. Определение. Дополнением множества А называется множество элементов универсального множества U, не принадлежащие А. Обозначение: А. Очевидно А = U \ A. Контрольные вопросы и устные упражнения
Понятие множества, его элемент. Что означает запись: а) а Ï М, б) сÎ В. Конечные и бесконечные множества. Пустое множество. Как его обозначают? Почему ¢ Равные множества. Как доказать, что два множества равны? Верно ли, что {1, 2, 3} = {3, 2, 2, 3, 1}?{1. 2, {1. 2}}={{1,2}, 2}? Способы задания множеств. Задайте различными способами множество натуральных чисел, меньших 5. Подмножество. Как проверить, что одно множество является подмножеством другого? Верно ли, что А подмножество В, где Универсальное множество.
Упражнения 1. 1. Запишите перечислением элементов: 1. Множество простых чисел первых двух десятков; 2. Множество букв в слове “ параллелограмм”; 3. Множество корней уравнения х2 = 25; 4. Множество цифр в числе 25252; 5. Множество целых чисел, заключенных между 65 и 75; 6. Множество натуральных делителей числа 3003. 1. 2. Поставьте вместо звездочки знак Î или Ï так, чтобы получилось верное высказывание: 35 * N, 15 * Z, -73 * Q, 1,73 * Z, 3,11 * Q,
1.3. Запишите с помощью перечисления элементов. 1. Множество правильных несократимых дробей со знаменателем 9; 2. Множество несократимых дробей с однозначным знаменателем, заключенных между числами 0 и 1/2.
1.4. Найдите множество корней уравнения; 1. (х - 1)(х - 2)(х - 3) = 0; 2. (х2 - 9)(х2 - 25) = 0; 3. х2 + 3 4. (х2 - 4х + 1) 5. х2 - 5( 6. х2 - 5 7. х + 8. 3х2 + |х - 2| = 2; 9. (х2 - 2х)(х - 1)2 = 12; 10. (х - 1)(х + 0,5)(х4 + 7) = 0 1.5. Запишите с помощью перечисления элементов множество: 1. А = {х | х Î N, х < 12}; 2. В = { х | х Î Z, |х | < 5; 3. C = { х | х = 3n, nÎ N, х < 33}; 4. D = { х | х = 5n + 1, nÎ N, х < 50}; 5. E = { x | 6. K = { x | | x - 3 | = 5 }; 7. 4 = { n | n Î Z; 8. М = {(х, y) | х + у - ху = 0, х, у, Î Z }; 9. N = {(х, у) | х2 - у2 = 3, х, у Î N}; 10. О = {(х, у) | х2 - 3ху + 2у2 = 3, х, у Î Z}.
1.6. Докажите, что множества А и В равны: 1. А = {у | у Î Z, |у| < 5}, В = { у | у Î Z, -7 < у - 2 < 3}; 2. А = {у | у = (а-3)(а+5), а Î Q}, В ={у | у=а2+2а-15,а ÎQ}; 3. А = {х | х = 8к -3, к Î Z}, В = {х | х = 8n + 5, n Î Z}
1.7. Среди множеств выделите равные: А = { х | х Î Z, х2 £ 25 }; В = { х | х Î Z, -3 £ х £ 5}; C = { х | х Î Z, | х | £ 5 }; D = { х| [Î Z,|х-1| £ 4 }.
1.8. Что представляет собой множество точек плоскости: 1. равноудаленных от двух точек А и В; 2.равноудаленных от трех точек А,В и С, не лежащих на одной прямой; 3. равноудаленных то трех точек А, В и С, лежащих на одной прямой; 4. равноудаленных от сторон угла АОВ?
1.9. В каких координатных углах расположены точки, принадлежащие множеству: 1. { (х; у) | х Î N, у Î N }; 2. { (х; у) | х Î Z, у Î N }; 3. { (х; у) | х Î Q, у Î Q, у £ 0 }; 4. { (х; у) | х Î Q, у Î Q, у ³ 0 }.
1.10. Постройте в координатной плоскости множество точек: 1. { (х; у) | х Î Z, у Î Z, -2 £ х £ 2, -2 £ у £ 2 }; 2. { (х; у) | х - любое число, у = 3 }; 3. { (х; у) | х = 2, у - любое число }; 4. { (х; у) | 1 £ х £ 2, у - любое число }.
1.11. Найдите множество решений системы уравнений: 1. (х + 1)2 - (х - 2)2 = 9 2. (х - 2)2 - (х + 3)2 = 10 (у + 1)2 - (у - 1)2 = 4 (у + 5)2 - (у - 5)2 = 48.
1.12. Найдите n(А), если: 1. А - множество натуральных делителей числа 28, 2. А - множество трехзначных чисел; 3. А - множество цифр в записи числа 11010100; 4. А - множество букв в слове “ математика”; 5. А - множество корней уравнения х2 + 1 = 0;
1.13. Сколько элементов содержит множество В, если: 1. В - множество простых двузначных чисел; 2. В - множество простых делителей числа 1001?
1.14. Известно, что х Î А и х Î В. Следует ли отсюда, что: 1. А Ì В; 2. В Ì А; 3. А = В? Изобразите на кругах Эйлера. Объясните, почему А = {2, 4, 6} является подмножеством множества В = {2, 4, 6,7}, но С = {4, 6, 8} не будет подмножеством В.
1.15. Изобразите с помощью кругов Эйлера отношения между множествами А и В, если: 1. А - множество натуральных чисел, В - множество чисел, кратных 5 (5Z); 2. А - множество прямоугольников, В - множество квадратов; 3. А - множество прямоугольников, В - множество прямоугольных треугольников.
1.16. Каковы отношения между множествами N, Z, Q, R? Изобразите эти отношения на кругах Эйлера.
1.17. Выпишите все подмножества множества А, если: 1. А = {а}; 2. А ={а, в}; 3. А ={ 1, 2, 3 }; 4. А ={{1};{2; 3}}. Чему равно количество подмножеств n - множества?
1.18. Для множеств А и В выясните, какие из утверждений: А Ì В, В Ì А, А = В, - верны: а) б) в) г)
1.19. Докажите: 1. если А Ì В, В Ì С, С Ì А, то А = В = С; 2. если А Ì В, В Ì С, С ¹ В, то С ¹ А; 3. если А Ì В, то (А Ç С) Ì (В Ç С); 4. если А Ì В, то (А \ С) Ì (В \ С).
1.20. Подмножества конечного множества называются сочетаниями. С1n - число одноэлементных подмножеств множества из n элементов; С2n - число 2 -элементных подмножеств, С3n - число 3 - элементных подмножеств. 1. Задано множество А = { а, в, е}. Выпишите одноэлементные, 2- элементные, 3-элементные подмножества. Найдите С 03, С13, С23, С33, С03 + С13 + С23 + С33, 2. А = { а, в, с, d,е }. Убедитесь: С 05 = С 55; C15 = C 45, С25 = С35. Чему равен х, если Скn = Cхn?
З А Н Я Т И Е № 2. Операции над множествами Правило суммы
При решении практических задач часто приходится выбирать из некоторого множества его подмножества, распределять элементы множества в том или ином порядке и т.д. Так как в этих задачах речь идёт о тех или иных комбинациях объектов, их называют комбинаторными задачами. Раздел математики, в котором изучаются комбинаторные задачи, называют комбинаторикой. ЗАДАЧА. На тарелке лежат 6 яблок и 5 груш. Сколькими способами можно выбрать один плод? РЕШЕНИЕ. Так как в задаче идёт речь о выборе “яблока или груши”, то его можно осуществить 6 + 5 = 11 способами.
Справедливо следующее утверждение: Правило суммы. Если элемент а можно выбрать m способами, а элемент b - n способами, причём любой выбор элемента а отличен от любого выбора элемента b, то выбор “ а или b ” можно сделать m + n способами. Это же правило на языке теории множеств формулируется так: Теорема. Если пересечение конечных множеств А и В пусто, А Ç В = А Ç В =
Множества могут иметь и непустое пересечение. Для двух множеств ситуацию характеризует Теорема. Для любых конечных множеств А и В верно равенство: n(A È B) = n(A) + n(B) - n(A Ç B). (1) Доказательство, Множество А È В есть объединение трёх не
пересекающихся множеств: А \ (А Ç В), А Ç В и В \ (А Ç В). Каждое из них соответственно имеет элементов: n(A) - n(A Ç B), n(A Ç B) и n(B) - n(A Ç B). Следовательно, число элементов во множестве А È В равно: n(A) - n(A Ç B) + n(A Ç B) + n(B) - - n(A Ç B) = n(A) + n(B) - n(A Ç B) Формула (1) есть частный случай для двух множеств и её можно распространить на любое конечное число элементов. Например, для трёх множеств А, В и С: n(A È B È C) = n(A) + n(B) + n(C) - - n(A Ç B) - n(A Ç C) - n(B Ç C) + n(A Ç B Ç C). Обоснуйте этот факт на кругах Эйлера! Правило произведения Определение. Прямым произведением двух множеств А и В называется множество всех упорядоченных пар (а; в) таких, что а Î А и в Î В. Обозначение: А А Аналогично определяется прямое произведение n множеств А1´А2´...´Аn = { (a1,a2,...,an) | a1 Î A1, a2 Î A2,..., an Î An } Здесь: (а1, а2,..., аn) - упорядоченная n-ка. Считаем, что (а; в) = (а1; в1), если а = а1 и в = в1. ПРИМЕР. Найдите А ´ В, если А = { 1, 2 }, b = { a, b, c }. ОТВЕТ: По определению А´В = { (1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}.
Пусть А и В - числовые множества. Тогда элементы прямого произведения этих множеств будут упорядоченными парами чисел, которые можно изобразить на плоскости и получить фигуру. ПРИМЕР. Изобразите на координатной плоскости А ´ В, если: а) А = { 1, 2, 3 }, B = { 2, 4 }; б) А = { 1, 2, 3, 4 }, B = [ 1; 4 ]; в) А = [ 1; 3 ], B = [ 1; 4 ]. ОТВЕТ: Результаты изображены:
у у у 4 4 4 3 3 3 2 2 2 1 1 1 1 2 3 4 5 х 1 2 3 4 5 х 1 2 3 4 5 х а) б) в) Как найти число элементов прямого произведения двух множеств? Рассмотрим это на примере. Пусть А = {a, d, c}, т.е. n(A) = 3 и В ={p, q}, где n(B) = 2. Выпишем все элементы множества А ´ В:
(a, p) (b, p) (c, p) (a, q) (b, q) (c, q) В этой таблице n(A) столбцов и n(B) строк. Поэтому n(A ´ B) = n(A) . n(B)
Можно сформулировать и более общее утверждение Теорема. Если А1, А2,..., Аn - конечные множества, то n(A1´ A2´...´ An) = n(A1) . n(A2) . ... . n(An).
ЗАДАЧА. Сколько двузначных чисел можно образовать используя только цифры 0, 1, 2,? РЕШЕНИЕ. Первую цифру двузначного числа мы можем выбрать только из множества А = { 1, 2 } (почему?), а вторую цифру из множества В = {0, 1, 2 }. Получим: 10, 11, 12, 20, 21, 22. Их шесть. n(A ´ B) = n(A) . n(B) = 2.3 = 6.
Решение таких задач можно проводить на основе следующего утверждения, обобщающего теорему: Правило произведения. Если первый элемент а1 упорядоченной n-ки можно выбрать m1 способом, второй элемент а2, после выбора а1, - m2 способами (независимо от того, как выбран а1)и т.д., элемент аn, после выбора а1, а2,..., аn-1 и независимо от того, как они выбраны,- mn способами, то общее число получаемых n-ок равно m = m1m2...mn. Без повторений
ЗАДАЧА. Сколькими способами можно упорядочить элементы множества А = {a, b, c}? РЕШЕНИЕ. Очевидно, этих способов 6: abc, acb, bac, bca,cab, cba. Это число можно найти и, используя правило произведения: n = 3.2.1 = 3! = 6. (Смотрите также задачу № 68.) Определение. Последовательность, состоящая из всех различных элементов множества, называется его перестановкой. Например, (1; 5; 2; 4; 3) - одна из перестановок множества А = { 1; 2; 3; 4; 5 }. Число различных перестановок множества, состоящего из n элементов, обозначается Рn. Мы видим, что: Рn = n! Найдём все трёхэлементные подмножества множества {a, b, c, d }. Это: {a,b,c}, {a,c, d}, {a,b,d}, {b,c,d}. Итак, число таких подмножеств равно 4. Пусть n(A) = n. Обозначим через r число k-элементных подмножеств множества А. Пусть m - число упорядоченных наборов из k элементов множества А. По правилу произведения m = n.(n -1).....(n - k + 1) Как связаны числа r и m? Очевидно, m = k!.r. Откуда: r = Определение. k-элементные подмножества n-элементного множества А (k £ n) называются сочетаниями без повторений из элементов этого множества по k. Число таких подмножеств обозначается: Сnk. Cnk =
Контрольные вопросы и устные упражнения Свойства операций над множествами. В чем заключается двойственный характер этих свойств? Число элементов объединения множеств. Правило суммы. Упражнения 2.1. Найдите пересечение, объединение, разность множеств А и В, если: 1. А = { 1, 2, 3, 4, 5}, В = {3, 4, 5, 6, 7}; 2. А - множество двузначных чисел, кратных 5 и В - множество двузначных чисел, кратных 3; 3. А = { х | х Î N, х < 37}, В = { х | х Î N, х > 28 }. 2.2. Пусть R - универсальное множество, А = (-1; 3], В = [0; 5). Найдите: 1. А Ç В; 2. А \ В; 3. 6. А È В; 7. В \ А; 8. 2.2. Какие элементы входят в пересечение, объединение множеств букв в словах: 1. математика и грамматика; 2. ворона и сорока; 3. насос и сосна; 4. ветка и роща? 2.3. Изобразите на координатной прямой множества А и В, их пересечение, объединение, разность, а также
2.4. Начертите два треугольника так, чтобы их пересечением: 1) была точка; 2) был отрезок; 3) был треугольник; 4) был четырехугольник.
2.5. Даны множества: А = {15, 17, 18, 21, 29}, В = {12, 17, 21, 37, 43}, С = {18, 21, 29, 43}. Найдите пересечение, объединение, разность множеств А и В, А и С, В и С, а также А Ç (В È С) и А È(В Ç С).
2.6. Какая фигура образуется в пересечении множеств точек {(х, у) | 0 £ у } и {(х, у)| 0 £ х + у £ 5}?
2.7. Дано: А = (0; 1) È [2; ¥), В = [0,5; 3), U = R. Найдите А È В, А Ç В, В \ А, А \ В,
2.8. Дано: А = {1, 2, 3, 4}, В = {3, 4, 5, 6}; C = {1, 3, 5}, U = {1, 2, 3, 4, 5, 6, 7}. Найдите А \ В,
2.9. Докажите следующие свойства: 1. А \ (В È С) = (А \ В) Ç (А \ С) 2. А È (В \ А) = А È В 3. дистрибутивность объединения относительно пере- сечения. 4. дистрибутивность пересечения относительно объединения. 5. А Ç 7. А \ В = 9. А \ В = А Ç
2.10. Докажите равенство множеств при помощи основных свойств операций. 1. (А È В) Ç 3. (А Ç В) È (
2.11. Упростите запись множеств при помощи основных свойств операций. 1 3. (
7.
2.12. Можно ли доказать равенство или включение множеств с помощью диаграмм Эйлера-Венна? Проиллюстрируйте равенство множеств: 1. А Ç (В Ç С) = (А Ç В) Ç С 2. А Ç (В ÈС)= (А ÇВ) È(А ÇС) 3. А È 5. А \ В = А Ç
2.13. Решите уравнения для X Ì И. 1. 5. х È х = х 6. х Ç 8. х Ç (1, 3) = (1, 2) 9. х \ (1, 3) = [1; 2]
2.14. Докажите, что А Ì В. Почему В не будет подмножеством А. 1. А = (\ У) Ç(С \ Д), В = Х Ç С. 2. А = (Х \ У) \ С, В = Х Ç 3. А = Х Ç У, В = (Х È У) \ (Х \ У) 4. А = Х Ç (У \ С), В = (Х È У) \ (Х Ç С).
2.15. Запишите двойственные формулы. Используя свойства операций над множествами, докажите: 1. (А Ç В) È В = В; 2. (А Ç 3..(А Ç В) È (А Ç В) È А = А; 4. (А È В) Ç 5. 6. (А Ç В) È 7. (А Ç В) È (
2.16. Можно ли узнать число участников шахматных соревнований, если в них было: 1. 20 юношей и 12 девушек, 2. 20 юношей и 27 школьников?
2.17 Экзамен по математике сдавали 250 школьников. Оценку ниже 5 получили 180 человек, а выдержали этот экзамен 210 школьников. Сколько человек получили оценки 3 и 4?
2.18. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 -на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на лыжах, и на коньках?
2.19. В группе из 100 туристов 70 человек знают английский язык, 45 знают французский и 23 знают оба языка. Сколько человек не знают ни английского ни французского языка?
2.20. В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили торт и коробку конфет?
2.21. В отряде из 40 человек 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого. Сколько ребят умеет плавать и играть в шахматы?
2.22. Найдите n А Ç В Ç С), если известно, что n(А)=13, n(В) = 18, n(С) = 9, n(А È В È С) = 40.
2.23. На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги А, В и С. Результаты опроса оказались таковы: книгу А читало 25 учащихся, книгу В - 22, книгу С - также -22. Книгу А или В читали 33 ученика, А или С - 32, В или С 31; все три книги прочитали 10 учащихся. Сколько учеников прочли только по одной книге? Сколько учащихся не читали ни одной из этих трех книг?
2.24. Сколько среди первых 50 натуральных чисел не делятся ни на 2, ни на 3, ни на 5?
2.25. В спортивном лагере 65% ребят умеют играть в футбол, 70% в волейбол, 75% - в баскетбол. Каков наименьшее число ребят, умеющих играть и в футбол, и в волейбол, и в баскетбол?
2.26. Сколько чисел среди первой сотни натуральных не делятся ни на 2, ни на 3, ни на 5, ни на 7?
2.27. Найдите множество решений уравнений: 1.
3. х2 - 7 |х| = 0 4. 2х2 + |х| = 0
5. х2 - 7. х2 + 3 9. х = 3
2.28. Найдите решения неравенств, запишите их в виде промежутков и изобразите на числовой оси: 1. - 2х + 21 > 0; 2. 18 - 3х £ 0;
3.
5. (
7. |х - 2| > 0; 8. |х + 2| £ 3;
9. |5х - 1| ³ - 3; 10. |х - 3| £ -1.
2.29. Найдите область определения функций 1. у =
2. у =
3. у =
2.30. Решите систему неравенств 1.
3. 5.
7.
9. 2.31. Придумайте систему двух неравенств, решением которой является промежуток: 1. (- 3; 0,5]; 2. (- ¥; 1); 3. [ -1; 5 ]; 4. [- 3; + ¥).
2.32. Решите совокупность неравенств: 1. 3. 4. 5. 6. 7.
8. 10.
12.
2.33. Решите неравенства: 1. | х |(3х + 2) > 0; 2. | х-3 |(7х - 4) £ 0; 3. (9х2 + 12х + 4)(3х - 2) ³ 0; 4. (20х - 4х2 - 25)(3х - 8) £ 0; 5. | х2 - 36 | (3 - х) ³ 0; 6. | х2 - 9 | (2х - 3) > 0; 7. 8. З А Н Я Т И Е № 3.
Упражнения 3.1. Выясните логическую структуру следующих предложений: 1. число 9 является рациональными или иррациональными; 2. если углы вертикальные, то они равны; 3. треугольник АВС равнобедренный или прямоугольный; 4. число 56 не делится на 9; 5. если число целое и положительное, то оно натуральное.
3.2. Сформулируйте отрицание следующих высказываний: 1. 257 - четное число; 2. число 3. число 23 делится на 7; 4. число 9 положительно; 5. 3 > 5: 6. 5 + 3 = 8; 7. 30 - простое число; 8. Луна больше Земли; 9. Аня старше Тани; 10. 2 ³ 10. Укажите, что является истинным: само высказывание или его отрицание.
3.3. Для каждого из следующих высказывании составьте отрицание, а затем двойное отрицание. Убедитесь, что двойное отрицание совпадает по смыслу с исходным высказыванием. 1. 15 делится на 3; 2. 5 - положительное
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 912; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.58 (0.015 с.) |

 . Примером пустого множества может служить множество коней уравнения: 2х + 5 = 2(х - 1).
. Примером пустого множества может служить множество коней уравнения: 2х + 5 = 2(х - 1).








 Изображение:
Изображение:


 а) отрезка от a до b (обозначение: [ a; b ]); определяющее неравенство: a £ x £ b; изображение:
а) отрезка от a до b (обозначение: [ a; b ]); определяющее неравенство: a £ x £ b; изображение:
 a b x
a b x



 a b x
a b x


 {¢}
{¢} ,
,  ? Какое подмножество называется собственным? несобственным? Приведите примеры.
? Какое подмножество называется собственным? несобственным? Приведите примеры.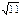 * Q,
* Q,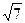 * R, е * Q,p * Q,
* R, е * Q,p * Q,  Sin
Sin  * Z, 1234 * Z,
* Z, 1234 * Z,  * Q
* Q +
+  * N, -123456 * 3Z.
* N, -123456 * 3Z. х + 4 = 0;
х + 4 = 0; = 0;
= 0; )2 - 14 = 0;
)2 - 14 = 0; - 14 = 0;
- 14 = 0; = 0;
= 0; -
- 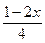 > x, x Î Z, x < 19 };
> x, x Î Z, x < 19 };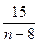 Î Z };
Î Z }; ,
, 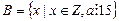 ;
;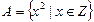 ,
,  ;
; ,
,  ;
; ,
,  ?
?
 В.
В.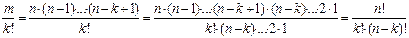
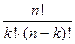
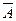 ; 4.
; 4.  ;
;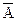 и
и 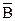 , если А = {х | 2 £ х £ 6}, В = {х | 4 £ х £ 8}.
, если А = {х | 2 £ х £ 6}, В = {х | 4 £ х £ 8}. = И.
= И.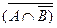 È В 2. ((А È(В È С)) Ç А) È
È В 2. ((А È(В È С)) Ç А) È 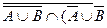 4.
4. 
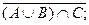 6.
6. 
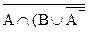 ) È В
) È В 
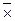 = Æ; 2.
= Æ; 2. 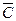
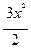 =
=  ; 2.
; 2. 
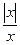 = 0, 6. х2 +
= 0, 6. х2 + 
 8. х2 - 5
8. х2 - 5 
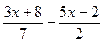 < х; 4.
< х; 4. 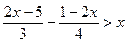 ;
; - 2) х ³ 2
- 2) х ³ 2 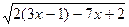


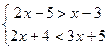 2.
2. 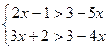
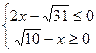 4.
4. 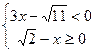
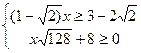 6.
6. 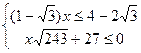
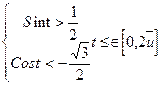 8.
8. 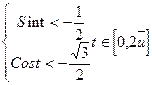
 10.
10. 
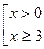 2.
2. 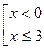
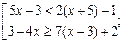
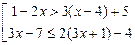
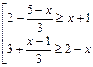 .
.
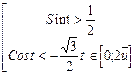
 9.
9. 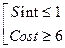
 11.
11. 
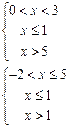 13.
13. 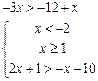

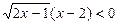 ;
;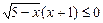 .
.


