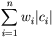Тема: перевод из одной системы счисления в другую.

Лабораторные работы

 

Лабораторная работа №1.

Тема: Перевод из одной системы счисления в другую.

Цель: научиться переводить числа из одной системы счисления в другую.

 

Методические указания.

Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.

Все системы счисления делятся на позиционные и непозиционные.

Непозиционными системами являются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе. Примером непозиционной системы счисления является римская система. К недостаткам таких систем относятся наличие большого количества знаков и сложность выполнения арифметических операций.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяющееся позицией цифры в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону. Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.

Количество p различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления "p".

В десятичной системе используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; эта система имеет основанием число десять.

Задание 1. Запишите развернутую и краткую формы записи любого числа.

В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную. В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое 1. Поэтому основной системой счисления применяемой в ЭВМ является двоичная система.

Двоичная система счисления. Используется две цифры: 0 и 1.

Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7.

Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таблица 1).

Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр латинскими

буквами: 10=A,

11=B,

12=C,

13=D,

14=E,

15=F.

Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (Таблица 1).

 

Таблица 1. Наиболее важные системы счисления.

Перевод чисел из одной системы счисления в другую.

Перевод чисел в десятичную систему осуществляется путем составления

степенного ряда с основанием той системы, из которой число переводится. Затем

подсчитывается значение суммы.

Задание 2.

Перевести 10101101.101 из «2» в «16», «8» и «10» с.с.

При одновременном использовании нескольких различных систем счисления основание системы, к которой относится число, указывается в виде нижнего индекса.

Задание 3. Переведите самостоятельно.

а) Перевести 703.048 из «10» в «2», затем в «8» и наконец, в «16»

б) Перевести B2E.416 из «16» в «10», затем в «8».

Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.

Задание 4.

а) Перевести 18110 из «10» в «2».

б) Перевести 62210 из «8» в «2», затем в «10».

Перевод правильных дробей из десятичной системы счисления в недесятичную.

Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.

Задание 5. Перевести 0.312510

Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.

Задание 6. Перевести 0.6510 из «10» в «2» с.с. Точность 6 знаков.

Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.

Задание 7.

Перевести 23.12510 из «10» в «2» с.с.

Необходимо отметить, что целые числа остаются целыми, а правильные дроби дробями в любой системе счисления. Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.

Задание 8.

а)Перевести 305.47 из «8» в «10» с.с.

б)Перевести 7B2.E16 из «16» в «10».

Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.

Задание 9.

а) Перевести 1101111001.1101 из «2» в «8» с.с.

б) Перевести 11111111011.100111 из «2» в «16» с.с.

Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.

Задание 10.

Перевести 175.248 "16" с.с.

Двоичная арифметика.

При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.

Задание 11. Выполнить сложение двоичных чисел:

а) X=1101, Y=101;

б) X=1101, Y=101, Z=111;

При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.

Задание 12. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.

Пример. 1001* 101=?

Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.

Пример. 1100.011: 10.01=

Самостоятельная работа.

Выполнить перевод числа в соответствии с вариантом.

1. Перевести десятичное число А=121 в двоичную систему счисления.

2. Перевести двоичное число А=10001010111,01 в десятичную систему

счисления.

3. Перевести десятичное число А=135,656 в двоичную систему счисления с

точностью до пяти знаков запятой.

4. Перевести двоичное число А=10111011 в десятичную систему счисления

методом деления на основание.

5. Перевести восьмеричное число А=345,766 в двоичную систему счисления.

6. Записать десятичное число А=79,346 в двоичнодесятичной

форме.

7. Перевести десятичную дробь 64

A = 63 9 в двоичную систему счисления.

8. Перевести десятичное число А=326 в троичную систему счисления.

9. Перевести десятичную дробь 40

A = 63 5 в двоичную систему счисления.

10. Перевести десятичное число А=15,647 в двоичную систему счисления.

11. Перевести десятичное число А=1211 в пятеричную систему счисления.

12. Перевести десятичную дробь А=0,625 в двоичную систему счисления.

13. Перевести двоичную дробь А=0,1101 в десятичную систему счисления.

14. Перевести десятичное число А=113 в двоичную систему счисления.

15. Перевести двоичное число А=11001,01 в десятичную систему счисления.

16. Перевести десятичное число А=96 в троичную систему счисления.

Методические указания.

В связи с разными подходами к определению информации выделяют два подхода к измерению информации.

Краткие сведения из теории.

Шифры простой замены

Система шифрования Цезаря - частный случай шифра простой замены. Метод основан на замене каждой буквы сообщения на другую букву того же алфавита, путем смещения от исходной буквы на K букв.

Известная фраза Юлия Цезаря

VENI VI D I VICI, где

A

B

C

D

E

F

G

H

I

G

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

 

пришел, увидел, победил, зашифрованная с помощью данного метода, преобразуется в

SBKF SFAF SFZF

при смещении на 4 символа влево.

Греческим писателем Полибием за 100 лет до н.э. был изобретен так называемый полибианский квадрат размером 5*5, заполненный алфавитом в случайном порядке. Греческий алфавит имеет 24 буквы, а 25-м символом является пробел. Для шифрования на квадрате находили букву текста и записывали в зашифрованное сообщение букву, расположенную ниже ее в том же столбце. Если буква оказывалась в нижней строке таблицы, то брали верхнюю букву из того же столбца.

 

M	T	L	E	X
A	K	F	Q	Y
N	B	R	O	W
C	J	H	D	P
U	I	S	G	V

 

Схема шифрования Вижинера. Таблица Вижинера представляет собой квадратную матрицу с n² элементами, где n — число символов используемого алфавита. На рисунке показана верхняя часть таблицы Вижинера для кириллицы. Каждая строка получена циклическим сдвигом алфавита на символ. Для шифрования выбирается буквенный ключ, в соответствии с которым формируется рабочая матрица шифрования.

 

а

б

в

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

б

в

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

в

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

в

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

в

г

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

в

г

д

И т.д. до 33-ей строки..

Таблица Вижинера

 

Осуществляется это следующим образом. Из полной таблицы выбирается первая строка и те строки, первые буквы которых соответствуют буквам ключа. Первой размещается первая строка, а под нею — строки, соответствующие буквам ключа в порядке следования этих букв в ключе шифрования. Пример такой рабочей матрицы для ключа «книга» приведен на Рис. 3.1.3.

Процесс шифрования осуществляется следующим образом:

1. под каждой буквой шифруемого текста записываются буквы ключа. Ключ при этом повторяется необходимое число раз.

2. каждая буква шифруемого текста заменяется по подматрице буквами находящимися на пересечении линий, соединяющих буквы шифруемого текста в первой строке подматрицы и находящимися под ними букв ключа.

3. полученный текст может разбиваться на группы по несколько знаков.

Пусть, например, требуется зашифровать сообщение: максимально допустимой ценой является пятьсот руб. за штуку. В соответствии с первым правилом записываем под буквами шифруемого текста буквы ключа. Получаем:

максимально допустимой ценой является пятьсот руб. за штуку

книгакнигак нигакнигак нигак нигакниг акнигак ниг ак нигак

а

б

в

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

в

г

д

е

ё

ж

з

и

й

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

в

г

д

е

ё

ж

з

и

й

к

л

м

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

в

г

д

е

ё

ж

з

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

а

б

в

а

б

в

г

д

е

ё

ж

з

и

й

к

л

м

н

о

п

р

с

т

у

ф

х

ц

ч

ш

щ

ъ

ы

ь

э

ю

я

 

Дальше осуществляется непосредственное шифрование в соответствии со вторым правилом, а именно: берем первую букву шифруемого текста (М) и соответствующую ей букву ключа (К); по букве шифруемого текста (М) входим в рабочую матрицу шифрования и выбираем под ней букву, расположенную в строке, соответствующей букве ключа (К),— в нашем примере такой буквой является Ч; выбранную таким образом букву помещаем в зашифрованный текст. Эта процедура циклически повторяется до зашифрования всего текста.

Эксперименты показали, что при использовании такого метода статистические характеристики исходного текста практически не проявляются в зашифрованном сообщении. Нетрудно видеть, что замена по таблице Вижинера эквивалентна простой замене с циклическим изменением алфавита, т.е. здесь мы имеем полиалфавитную подстановку, причем число используемых алфавитов определяется числом букв в слове ключа. Поэтому стойкость такой замены определяется произведением стойкости прямой замены на число используемых алфавитов, т.е. число букв в ключе.

Расшифровка текста производится в следующей последовательности:

1. над буквами зашифрованного текста последовательно надписываются буквы ключа, причем ключ повторяется необходимое число раз.

2. в строке подматрицы Вижинера, соответствующей букве ключа отыскивается буква, соответствующая знаку зашифрованного текста. Находящаяся под ней буква первой строки подматрицы и будет буквой исходного текста.

3. полученный текст группируется в слова по смыслу.

Нетрудно видеть, что процедуры как прямого, так и обратного преобразования являются строго формальными, что позволяет реализовать их алгоритмически. Более того, обе процедуры легко реализуются по одному и тому же алгоритму.

Одним из недостатков шифрования по таблице Вижинера является то, что при небольшой длине ключа надежность шифрования остается невысокой, а формирование длинных ключей сопряжено с трудностями.

Нецелесообразно выбирать ключи с повторяющимися буквами, так как при этом стойкость шифра не возрастает. В то же время ключ должен легко запоминаться, чтобы его можно было не записывать. Последовательность же букв не имеющих смысла, запомнить трудно.

С целью повышения стойкости шифрования можно использовать усовершенствованные варианты таблицы Вижинера. Приведем только некоторые из них:

· во всех (кроме первой) строках таблицы буквы располагаются в произвольном порядке.

· В качестве ключа используется случайность последовательных чисел. Из таблицы Вижинера выбираются десять произвольных строк, которые кодируются натуральными числами от 0 до 10. Эти строки используются в соответствии с чередованием цифр в выбранном ключе.

 

Известны также и многие другие модификации метода.

Алгоритм перестановки

Этот метод заключается в том, что символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока символов. Рассмотрим некоторые разновидности этого метода, которые могут быть использованы в автоматизированных системах.

Самая простая перестановка — написать исходный текст задом наперед и одновременно разбить шифрограмму на пятерки букв. Например, из фразы

ПУСТЬ БУДЕТ ТАК, КАК МЫ ХОТЕЛИ.

получится такой шифротекст:

ИЛЕТО ХЫМКА ККАТТ ЕДУБЪ ТСУП

В последней группе (пятерке) не хватает одной буквы. Значит, прежде чем шифровать исходное выражение, следует его дополнить незначащей буквой

(например, О) до числа, кратного пяти:

ПУСТЬ-БУДЕТ-ТАККА-КМЫХО-ТЕЛИО.

Тогда шифрограмма, несмотря на столь незначительные изменения, будет выглядеть по-другому:

ОИЛЕТ ОХЫМК АККАТ ТЕДУБ ЬТСУП

Кажется, ничего сложного, но при расшифровке проявляются серьезные неудобства.

Во время Гражданской войны в США в ходу был такой шифр: исходную фразу писали в несколько строк. Например, по пятнадцать букв в каждой (с заполнением последней строки незначащими буквами).

П У С Т Ь Б У Д Е Т Т А К К А

К М Ы Х О Т Е Л И К Л М Н О П

После этого вертикальные столбцы по порядку писали в строку с разбивкой на пятерки букв:

ПКУМС ЫТХЬО БТУЕД ЛЕИТК ТЛАМК НКОАП

Если строки укоротить, а количество строк увеличить, то получится прямоугольник-решетка, в который можно записывать исходный текст. Но тут уже потребуется предварительная договоренность между адресатом и отправителем посланий, поскольку сама решетка может быть различной длины-высоты, записывать к нее можно по строкам, по столбцам, по спирали туда или по спирали обратно, можно писать и по диагоналями, а для шифрования можно брать тоже различные направления.

Шифры сложной замены

Шифр Гронсфельда состоит в модификации шифра Цезаря числовым ключом. Для этого под буквами сообщения записывают цифры числового ключа. Если ключ короче сообщения, то его запись циклически повторяют. Зашифрованное сообщение получают примерно также, как в шифре Цезаря, но используют не одно жестко заданное смещение а фрагменты ключа.

Пусть в качестве ключа используется группа из трех цифр – 314, тогда сообщение

С О В Е Р Ш Е Н Н О С Е К Р Е Т Н О

3 1 4 3 1 4 3 1 4 3 1 4 3 1 4 3 1 4

Ф П Ё С Ь З О С С А Х З Л Ф З У С С

 

В шифрах многоалфавитной замены для шифрования каждого символа исходного сообщения применяется свой шифр простой замены (свой алфавит).

 

	АБВГДЕЁЖЗИКЛМНОПРСТУФХЧШЩЪЫЬЭЮЯ_
А	АБВГДЕЁЖЗИКЛМНОПРСТУФХЧШЩЪЫЬЭЮЯ_
Б	_АБВГДЕЁЖЗИКЛМНОПРСТУФХЧШЩЪЫЬЭЮЯ
В	Я_АБВГДЕЁЖЗИКЛМНОПРСТУФХЧШЩЪЫЬЭЮ
Г	ЮЯ_АБВГДЕЁЖЗИКЛМНОПРСТУФХЧШЩЪЫЬЭ
.	…………
Я	ВГДЕЁЖЗИКЛМНОПРСТУФХЧШЩЪЫЬЭЮЯ_АБ
_	БВГДЕЁЖЗИКЛМНОПРСТУФХЧШЩЪЫЬЭЮЯ_А

 

Каждая строка в этой таблице соответствует одному шифру замены аналогично шифру Цезаря для алфавита, дополненного пробелом. При шифровании сообщения его выписывают в строку, а под ним ключ. Если ключ оказался короче сообщения, то его циклически повторяют. Зашифрованное сообщение получают, находя символ в колонке таблицы по букве текста и строке, соответствующей букве ключа. Например, используя ключ АГАВА, из сообщения ПРИЕЗЖАЮ ШЕСТОГО получаем следующую шифровку:

ПРИЕЗЖАЮ_ШЕСТОГО

АГАВААГАВААГАВАА

ПОИГЗЖЮЮЮШЕПТНГО

Такая операция соответствует сложению кодов ASCII символов сообщения и ключа по модулю 256.

Задание

Придумайте 3 фразы, каждая минимум из 7 слов. Реализуйте шифрование этой фразы всеми перечисленными видами шифрования.

Текстовый редактор Блокнот

Открыть блокнот.

а) Используя клавишу Alt и малую цифровую клавиатуру раскодировать фразу: 145 170 174 224 174 255 170 160 173 168 170 227 171 235;

Технология выполнения задания: При удерживаемой клавише Alt, набрать на малой цифровой клавиатуре указанные цифры. Отпустить клавишу Alt, после чего в тексте появится буква, закодированная набранным кодом.

 

б) Используя ключ к кодированию, закодировать слово – зима;

Технология выполнения задания: Из предыдущего задания выяснить, каким кодом записана буква а. Учитывая, что буквы кодируются в алфавитном порядке, выяснить коды остальных букв.

Что вы заметили при выполнении этого задания во время раскодировки? Запишите свои наблюдения.

Цель работы: научиться вычислять информационный объем звуковых файлов, заданных различными характеристиками; вычислять время звучания звукового файла по его размеру; научиться работать с программой «Звукозапись» ОС Windows.

Методические указания.

С начала 90-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, может сохранять в виде файлов (файл - это определённое количество информации, хранящееся на диске и имеющее имя) и воспроизводить звуковую информацию. С помощью специальных программных средств (редакторов аудио файлов) открываются широкие возможности по созданию, редактированию и прослушиванию звуковых файлов. Создаются программы распознавания речи, и появляется возможность управления компьютером голосом.

Именно звуковая плата (карта) преобразует аналоговый сигнал в дискретную фонограмму и наоборот, «оцифрованный» звук – в аналоговый (непрерывный) сигнал, который поступает на вход динамика.

При двоичном кодировании аналогового звукового сигнала непрерывный сигнал дискретизируется, т.е. заменяется серией его отдельных выборок - отсчётов. Качество двоичного кодирования зависит от двух параметров: количества дискретных уровней сигнала и количества выборок в секунду. Количество выборок или частота дискретизации в аудиоадаптерах бывает различной: 11 кГц, 22 кГц, 44,1 кГц и др. Если количество уровней равно 65536, то на один звуковой сигнал рассчитано 16 бит (216). 16-разрядный аудиоадаптер точнее кодирует и воспроизводит звук, чем 8-разрядный.

Количество бит, необходимое для кодирования одного уровня звука, называется глубиной звука. Объём моноаудиофайла (в байтах) определяется по формуле:

При стереофоническом звучании объём аудиофайла удваивается, при квадрофоническом звучании – учетверяется.

По мере усложнения программ и увеличения их функций, а также появления мультимедиа-приложений, растёт функциональный объём программ и данных. Если в середине 80-х годов обычный объём программ и данных составлял десятки и лишь иногда сотни килобайт, то в середине 90-х годов он стал составлять десятки мегабайт. Соответственно растёт объём оперативной памяти.

Пример решения: Подсчитать, сколько места будет занимать одна минута цифрового звука на жестком диске или любом другом цифровом носителе, записанного с частотой

а) 44.1 кГц;

б) 11 кГц;

в) 22 кГц;

г) 32 кГц

И разрядностью 16 бит.

Решение.

а) Если записывают моносигнал с частотой 44.1 кГц, разрядностью 16 бит (2 байта), то каждую минуту аналого-цифровой преобразователь будет выдавать 441000 * 2 * 60 = 529 000 байт (около 5 Мб) данных об амплитуде аналогового сигнала, который в компьютере записываются на жесткий диск.

Если записывают стереосигнал, то 1 058 000 байт (около 10 Мб).

Задания.

1. Какой объем памяти требуется для хранения цифрового аудиофайла с записью звука высокого качества при условии, что время звучания составляет 3 минуты?

2. Какой объем данных имеет моноаудиофайл, длительность звучания которого 1 секунда, при среднем качестве звука (16 бит, 24 кГц)?

3. Рассчитайте объем стереоаудиофайла длительностью 20 секунд при 20-битном кодировании и частоте дискредитации 44.1 кГц. Варианты: 44,1 Mb, 4.21 Mb, 3,53 Mb.

4. Оцените информационный объем моноаудиофайла длительностью звучания 20 с, если "глубина" кодирования и частота дискретизации звукового сигнала равны соответственно 8 бит и 8 кГц;

5. Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен 700 Кбайт;

6. Запишите звуковой моноаудиофайл длительностью 20 с, с "глубиной" кодирования 8 бит и частотой дискретизации 8 кГц.

7. Определите качество звука (качество радиотрансляции, среднее качество, качество аудио-CD) если известно, что объем стериоаудиофайла длительностью звучания в 10 сек. Равен 940 Кбайт;

8. Оцените информационный объем стериоаудиофайла длительностью звучания 30 с, если "глубина" кодирования и частота дискретизации звукового сигнала равны соответственно 8 бит и 8 кГц;

9. Запишите звуковой файл длительностью 30с с "глубиной" кодирования 8бит и частотой дискретизации 8 кГц. Вычислите его объем и сверьтесь с полученным на практике значением.

10. Аналоговый звуковой сигнал был дискретизирован сначала с использованием 256 уровней интенсивности сигнала (качество звучания радиотрансляции), а затем с использованием 65536 уровней интенсивности сигнала (качество звучания аудио-CD). Во сколько раз различаются информационные объемы оцифрованного звука?

11. Оцените информационный объем моноаудиофайла длительностью звучания 1 мин. если "глубина" кодирования и частота дискретизации звукового сигнала равны соответственно:

16 бит и 48 кГц.

12. Запишите звуковой моноаудиофайл длительностью 1 минута с "глубиной" кодирования 16 бит и частотой дискретизации 48 кГц.

13. Подсчитать объем файла с 10 минутной речью записанного с частотой дискретизации 11025 Гц при 4 разрядном кодировании

14. Подсчитать время звучания звукового файла объемом 3.5 Мбайт содержащего стерео запись с частотой дискретизации 44100 Гц, 16-ти разрядном кодировании.

15. Определите количество уровней звукового сигнала при использовании 8-битных звуковых карт. Варианты: 256, 512,1024, 65 536.

16. Приведите пример:

а) аналогового способа представления звуковой информации;

б) дискретного способа представления звуковой информации.

17. Подготовить презентацию, демонстрирующую возможности звуковых форматов midi, wav, mp3, mod.

18. Перечислите параметры, от которых зависит качество двоичного кодирования звука.

Код Хаффмана

Определение 1: Пусть A={a₁,a₂,_...,a_n} - алфавит из n различных символов, W={w₁,w₂,_...,w_n} - соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C={c₁,c₂,_...,c_n}, такой что:

(1)	ci не является префиксом для cj, при i!=j

 

(2)

минимальна (|ci| длина кода ci)

называется минимально-избыточным префиксным кодом или иначе кодом Хаффмана.

Замечания:

1. Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины.

2. Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию.

3. В дальнейшем, чтобы избежать недоразумений, под кодом будем понимать битовую строку определенной длины, а под минимально-избыточным кодом или кодом Хаффмана - множество кодов (битовых строк), соответствующих определенным символам и обладающих определенными свойствами.

Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево.

Определение 2: Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана.

Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:

1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).

2. Из списка выберем 2 узла с наименьшим весом.

3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.

4. Добавим сформированный узел к списку.

5. Если в списке больше одного узла, то повторить 2-5.

Приведем пример: построим дерево Хаффмана для сообщения S="A H F B H C E H E H C E A H D C E E H H H C H H H D E G H G G E H C H H".

Для начала введем несколько обозначений:

1. Символы кодируемого алфавита будем выделять жирным шрифтом: A, B, C.

2. Веса узлов будем обозначать нижними индексами: A ₅, B ₃, C ₇.

3. Составные узлы будем заключать в скобки: ((A ₅+ B ₃)₈+ C ₇)₁₅.

Итак, в нашем случае A={ A, B, C, D, E, F, G, H }, W={2, 1, 5, 2, 7, 1, 3, 15}.

1. A ₂ B ₁ C ₅ D ₂ E ₇ F ₁ G ₃ H ₁₅

2. A ₂ C ₅ D ₂ E ₇ G ₃ H ₁₅ (F ₁+ B ₁)₂

3. C ₅ E ₇ G ₃ H ₁₅ (F ₁+ B ₁)₂ (A ₂+ D ₂)₄

4. C ₅ E ₇ H ₁₅ (A ₂+ D ₂)₄ ((F ₁+ B ₁)₂+ G ₃)₅

5. E ₇ H ₁₅ ((F ₁+ B ₁)₂+ G ₃)₅ (C ₅+(A ₂+ D ₂)₄)₉

6. H ₁₅ (C ₅+(A ₂+ D ₂)₄)₉ (((F ₁+ B ₁)₂+ G ₃) ₅+ E ₇)₁₂

7. H ₁₅ ((C ₅+(A ₂+ D ₂)₄) ₉+(((F ₁+ B ₁)₂+ G ₃) ₅+ E ₇)₁₂)₂₁

8. (((C ₅+(A ₂+ D ₂)₄) ₉+(((F ₁+ B ₁)₂+ G ₃) ₅+ E ₇)₁₂)₂₁+ H ₁₅)₃₆

В списке, как и требовалось, остался всего один узел. Дерево Хаффмана построено. Теперь запишем его в более привычном для нас виде.

 

 

ROOT

/\

0 1

/ \

/\ H

/ \

/ \

/ \

0 1

/ \

/ \

/ \

/ \

/\ /\

0 1 0 1

/ \ / \

C /\ /\ E

0 1 0 1

/ \ / \

A D /\ G

0 1

/ \

F B

Листовые узлы дерева Хаффмана соответствуют символам кодируемого алфавита. Глубина листовых узлов равна длине кода соответствующих символов.

Путь от корня дерева к листовому узлу можно представить в виде битовой строки, в которой "0" соответствует выбору левого поддерева, а "1" - правого. Используя этот механизм, мы без труда можем присвоить коды всем символам кодируемого алфавита. Выпишем, к примеру, коды для всех символов в нашем примере:

A=0010bin	C=000bin	E=011bin	G=0101bin
B=01001bin	D=0011bin	F=01000bin	H=1bin

Теперь у нас есть все необходимое для того чтобы закодировать сообщение S. Достаточно просто заменить каждый символ соответствующим ему кодом:

S^/="0010 1 01000 01001 1 000 011 1 011 1 000 011 0010 1 0011 000 011 011 1 1 1 000 1 1 1 0011 011 0101 1 0101 0101 011 1 000 1 1".

Оценим теперь степень сжатия. В исходном сообщении S было 36 символов, на каждый из которых отводилось по [log₂|A|]=3 бита (здесь и далее будем понимать квадратные скобки [] как целую часть, округленную в положительную сторону, т.е. [3,018]=4). Таким образом, размер S равен 36*3=108 бит

Размер закодированного сообщения S^/ можно получить воспользовавшись замечанием 2 к определению 1, или непосредственно, подсчитав количество бит в S^/. И в том и другом случае мы получим 89 бит.

Итак, нам удалось сжать 108 в 89 бит.

Теперь декодируем сообщение S^/. Начиная с корня дерева будем двигаться вниз, выбирая левое поддерево, если очередной бит в потоке равен "0", и правое - если "1". Дойдя до листового узла мы декодируем соответствующий ему символ.

Ясно, что следуя этому алгоритму мы в точности получим исходное сообщение S.

Метод RLE.

Наиболее известный простой подход и алгоритм сжатия информации обратимым путем - это кодирование серий последовательностей (Run Length Encoding - RLE). Суть методов данного подхода состоит в замене цепочек или серий повторяющихся байтов или их последовательностей на один кодирующий байт и счетчик числа их повторений. Проблема всех аналогичных методов заключается лишь в определении способа, при помощи которого распаковывающий алгоритм мог бы отличить в результирующем потоке байтов кодированную серию от других - некодированных последовательностей байтов. Решение проблемы достигается обы