
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевод целого числа из двоичной системы счисления в десятичную.Содержание книги
Поиск на нашем сайте
Пример. 1012 = 1*22 + 0*21 + 1*20 = 1*4 + 0 +1 = 510 Задание 12. Переведите число 1011012 в десятичную систему счисления. Решение. 1011012=1*25+0*24+1*23+1*22+0*21+1*20=32+8+4+1=4510 Ответ: 1011012=4510 Перевод целого числа из десятичной системы счисления в двоичную. Алгоритм 1. Последовательно выполнить деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя (т.е. меньшее 2). 2. Записать полученные остатки в обратной последовательности. Пример.Решение.
Задание 13. Как представляется число 2510 в двоичной системе счисления?
Решение.
2510=100112, что соответствует ответу №2. Ответ: 2. Перевод дробного числа из двоичной системы счисления в десятичную. Пример. 111,012 = 1*22 + 1*21 + 1*20 + 1*2-1 + 1*2-2 = 1*4 + 1*2 +1+ 0* = 4+2+1+0,5+0,25 = 7,7510 Перевод дробного числа из десятичной системы счисления в двоичную. Алгоритм. 1. Последовательно умножать (в исходной системе счисления) данное число и получаемые дробные части произведений на основание новой системы (на 2) до тех пор, пока дробная часть произведения не станет равной нулю или будет достигнута требуемая точность представления данного числа. 2. Полученные целые части произведений, являющиеся цифрами в числа в новой системе счисления, привести в соответствие с алфавитом новой системе счисления.
3. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
0,562510 = 0,10012.
 Решение. Решение.
Арифметические операции в двоичной и кратных ей системах счисления. Арифметические операции в позиционных системах счисления производится по единому алгоритму. Так, сложение двоичных чисел происходит по классическому алгоритму «столбиком» с переносом числа, кратного двум, единицей в следующий разряд. Рассмотрим этот алгоритм на примере двух двоичных чисел 10101012 и 1101112:
Результат сложения выглядит как 100011002. Проверим результат сложения, для чего переведем все числа в десятичную систему счисления: 10101012=8510, 1101112=5510, 100011002=14010, 8510+5510=14010. Двоичная система, являющаяся основой компьютерной арифметики, весьма громоздка и неудобна для использования человеком. Поэтому программисты используют две кратные двоичной системы счисления: восьмеричную и шестнадцатеричную. В случае шестнадцатеричной системы арабских цифр не хватает, и в качестве цифр используются первые шесть заглавных букв латинского алфавита. Примеры записи натуральных чисел от 1 до 16 в четырех системах счисления помещены в Таблице 2. Таблица 2. Примеры записи натуральных чисел от 1 до 16
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.27.24 (0.01 с.) |

 1
1
 0
0
 1
1
 0
0
 0
0
 0
0
 1
1
 0
0

 +1*
+1* 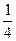 =
= 0,
0,



