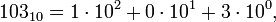Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Позиционные системы счисленияСодержание книги Поиск на нашем сайте
Позиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам. В более поздний период такая нумерация была развита индусами и имела неоценимые последствия в истории цивилизации. К числу таких систем относится десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман. Позиционная система счисления определяется целым числом Представление числа Целое число без знака
где Каждый базисный элемент Например, число сто три в десятичной системе счисления и в восьмеричной системе счисления записываются почти одинаково, а представляются по разному:
Запись числа Число
В ненулевых числах Во избежание путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса:
Построение такой записи числа называют позиционным кодированием числа, а саму запись — позиционным кодом числа. Примеры · 1 — единичная (унарная) система счисления, может рассматриваться как вырожденный случай позиционной системы счисления,
Перевод вещественного числа из десятичной системы счисления в двоичную систему
Рассмотрим число 567.25 и переведем его в двоичную систему счисления. Перевод целого числа из десятичной системы
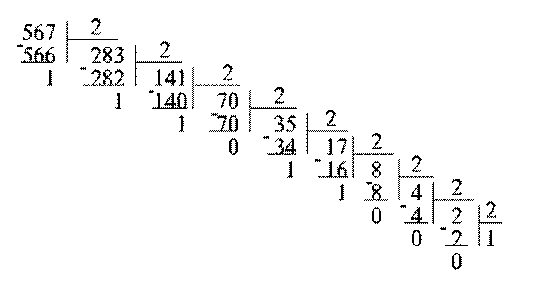
Целая часть числа равна 567. Будем последовательно делить это число, а затем частное на 2 до тех пор, пока это возможно, фиксируя при этом остаток от деления: 567:2 = 283 (остаток 1) 283:2 = 141 (остаток 1) 141:2 = 70 (остаток 1) 70:2 = 35 (остаток 0) 35:2 =17 (остаток 1) 17:2 = 8 (остаток 1) 8:2 = 4 (остаток 0) 4:2 = 2 (остаток 0) 2:2 = 1 (остаток 0) Теперь запишем число, начиная с последнего частного, приписывая ему остатки в противоположном порядке. Получим
56710 = 10001101112 Эти же операции можно записать последовательным делением в столбик:
Перевод дробной части вещественного числа из
Дробную часть, а затем дробные части получающихся произведений следует последовательно умножать на 2 до тех пор, пока очередная дробная часть произведения не окажется равной нулю или не будет достигнута нужная точность дроби. Целые части полученных произведений, записанные последовательно слева направо после запятой в искомом числе, образуют дробную часть искомого числа. Переводим дробную часть числа: 0.25 * 2 = 0. 50. 0.50 * 2 = 1. 00 (дробная часть числа равна 0, стоп). Записываем последовательно слева направо целые части полученных произведений 0.2510 = 0.012 Таким образом 567.2510 = 1000110111.012
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.173 (0.006 с.) |

 , которое называется основанием системы счисления. Система счисления с основанием
, которое называется основанием системы счисления. Система счисления с основанием  также называется
также называется  в системе счисления представляется в виде конечной линейной комбинации степеней числа
в системе счисления представляется в виде конечной линейной комбинации степеней числа 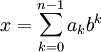 ,
, — это целые числа, называемые цифрами, удовлетворяющие неравенству
— это целые числа, называемые цифрами, удовлетворяющие неравенству 
 в таком представлении называется разрядом (позицией), старшинство разрядов и соответствующих им цифр определяется номером разряда (позиции)
в таком представлении называется разрядом (позицией), старшинство разрядов и соответствующих им цифр определяется номером разряда (позиции)  (значением показателя степени).
(значением показателя степени).