Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод математической индукции.
Индукцией (от латинского слова inductio - наведение) называется метод исследования, познания, связанный с обобщением результатов наблюдений и экспериментов. В умозаключениях от частного к общему анализ данных опыта, зафиксированный в посылках, “наводит” на существование в них общего, что и фиксируется в заключении. Заключение может быть как истинным, так и ложным. Речь идет об истинности предложения вида ("n)P(n) (*) на некотором множестве А. Если множество А конечно и содержит немного элементов, истинность утверждения (*) устанавливается, как правило, перебором элементов. П р и м е р 1. Доказать, что всякое четное натуральное число n, 4 £ n £ 100 представимо в виде суммы двух простых чисел. Достаточно рассмотреть: 4 = 2 + 2; 6 = 3 + 3; 8 = 3 + 5; 10 = 3 + 7;...; 98 = 5 + 93; 100 = 3 + 97. Доказательство проведено разбором всех возможных случаев.
П р и м е р 2. Французский математик Пьер Ферма (1601-1665) рассматривал числа вида f(n) = f(1) = f(4) =
Для бесконечного множества перебор невозможен и для доказательства истинности предложения (*) недостаточно проверить истинность Р(n) при n из какого-нибудь конкретного подмножества множества А. Более того, известны случаи, когда установление истинности Р(n) при всех n из достаточно широкого подмножества А1 множества А приводили к неверной гипотезе о том, что утверждение (*) истинно.
П р и м е р 3. На сколько частей делит пространство n плоскостей, проходящих через одну точку так, что никакие три из них не проходят через одну прямую? Одна плоскость делит пространство на две части. Две плоскости, проходящие через одну точку, делят пространство на 4-е части. Три плоскости, проходящие через одну точку, но не проходящие через одну прямую, делят пространство на 8 частей. Можно высказать утверждение, что для n = 1, n = 2, n = 3 число частей, на которое плоскости делят пространство равно 2n. Если сделать заключение, что n плоскостей разбивают пространство на 2n частей, то это предположение неверно.
П р и м е р 4. Рассмотрим ряд чисел вида b(n) = 991n2 + 1.
Подставляя вместо n числа натурального ряда, начиная с 1, мы не получим чисел, являющихся полным квадратом какого-либо другого числа, даже посвятив этому всю жизнь. И все же математик не имеет право утверждать, что все числа указанного вида не являются квадратами. Это строго оправдано. В данном случае число b(n) = 991n2 + 1 является полным квадратом при n = 12055735790331359447442538767.
П р и м е р 5. Пусть (an) - арифметическая прогрессия с разностью d: a1 = a1; a2 = a1 + d; a3 = a2 + d = a1 + 2d; a4 = a3 + d = = a1 + 3d. Гипотеза: an = a1 + (n -1)d. Проверка при n = 1, 2, 3,...позволяет выдвигать гипотезу, которая нуждается в проверке, ибо гипотеза может быть верной или неверной. Индукция - сильное и опасное оружие: велико искушение принять указанную закономерность без строгого обоснования, ведь опыты так убедительны! Примеры 2, 3, 4, где гипотезы неверны, служат хорошим лекарством от такого искушения
Метод перебора является полноценным доказательством, но невозможен, если случаев бесконечно много. В последнем случае задачи часто решаются с помощью метода математической индукции.
ТЕОРЕМА (Принцип математической индукции) Если на множестве натуральных чисел утверждение Р(n) удовлетворяет условиям: (а) P(1) истинно; (б) ("n)(P(n) ® P(n+1)) истинно, то истинно и предложение ("n) P(n). Справедливость принципа математической индукции следует из аксиом теории натуральных чисел. Более того, аналогичный принцип можно сформулировать и для высказывательной формы P(n) на множестве А, устроенном по типу множества натуральных чисел. ОПРЕДЕЛЕНИЕ. Говорят, что множество А устроено по типу множества натуральных чисел, если его элементы можно упорядочить так, что 1) есть первый элемент а1, 2) для каждого элемента а есть следующий за ним а/, 3) каждый элемент из А можно получить как следующий за а1 через конечное число шагов.
П р и м е р 6. А - множество четных неотрицательных чисел: а1 = 2, 2/ = 4, 4/ = 6 и т. д. П р и м е р 7. А = N \ { 1, 2, 3 }. a1 = 4, 4/ = 5, 5/ = 6,... П р и м е р 8. А = {-n | n Î N }. a1 = -1, (-1)/ = -2, (-2)/ = -3, (-3)/ = -4,... П р и м е р 9. A = Z. a1 = 0, 0/ = 1, 1/ = -1, (-1)/ = 2, 2/ = -2, (-2)/ = 3, 3/ = -4,...
ТЕОРЕМА (Принцип математической индукции в более общей форме) Пусть P(n) - высказывательная форма на множестве А устроенном по типу множества натуральных чисел такая, что
(а) Р(а1) истинно; (б) ("n)(P(n) ® P(n/)) истинно, тогда истинно и предложение ("n) P(n).
На сформулированном принципе основан метод доказательства, называемый методом математической индукции. Доказательство уже сформулированных утверждений методом математической индукции разбивается на четыре части. 1. Проверка того, что доказываемое утверждение P(а1) верно для первого элемента множества А. Эту часть доказательства называют базисом индукции. 2. Предположение, что доказываемое утверждение верно при некотором значении k Î А. Индукционное предположение. 3. Доказательство того, что утверждение верно для следующего элемента из множества А, т.е. истинно Р(a/). Индукционный шаг: P(k) Þ P(k+1). 4. Вывод: доказываемое утверждение истинно на основании принципа математической индукции.
Метод математической индукции применяется при решении задач на суммирование; задач, связанных с рекуррентным способом задания последовательности; при доказательстве тождеств и неравенств; выводе формул n -ого члена и суммы n первых членов арифметической и геометрической прогрессий; при решении задач на делимость и некоторые геометрические задачи, при доказательстве ряда математических утверждений и теорем. Теоретические вопросы: Принцип математической индукции. Различные формы метода математической индукции. П р и м е р 11. Доказать, что число 7n+1 + 82n-1 делится на 19 при любом натуральном n. Решение. 1. Доказываемое утверждение верно при m = 1, так как 72 + 81 = 57 и 57 делится на 19. 2. Предположим, что данное утверждение верно при некотором значении m = k, где k > 1, т.е. выражение р(k) = 7k+1 + 82k-1 делится на 19. 3. С учетом сделанного предположения докажем, что выражение р(n) = 7n+1 + 82n-1 делится на 19 при n = k + 1, т.е. 7k+2 + 82k+1 делится на 19. Действительно, 7k+2 + 82k+1 = 7. 7k+1 + 64. 82k-1 = 7. (7k+1 + 82k-1) + + 57.82k-1. Каждое слагаемое полученной суммы делится на 19: первое по индукционному предположению и 57 делится на 19, поэтому и 7k+2 + 82k+1 также делится на 19. 4. На основании принципа математической индукции можно сделать вывод, что исходное выражение р(n) делится на 19 при любом натуральном значении n.
Условимся о следующем: если даны n чисел а1, а2,..., аn, то вместо записи их суммы в виде а1 + а2 +... + аn, мы будем использовать обозначение П р и м е р 2. Докажем, что Решение П е р в ы й с п о с о б. Обозначим данное утверждение через P(n), где nÎN. При п = 1 левая часть формулы принимает вид 13,т.е. равна 1. Правая часть формулы при п = 1 принимает вид 12(1+1)2/4 и тоже равна 1. Итак, Р(1) истинно. Предположим, что это утверждение верно при п = k, т.е. что верно равенство Докажем, что P(k) Þ P(k+1) для k Î N. Имеем: 13 + 23 +...+ k3 + (k +1)3 = Итак, утверждение справедливо при п = 1, и из его справедливости для n = k следует, что оно верно и при n = k + 1. Значит, утверждение справедливо для любого натурального значения n. В т о р о й с п о с о б. Введем обозначения: А(n) = При n = 1: А(1) =13 = 1, В(1) = Пусть A(k) = B(k). Докажем, что A(k+1) = B(k+1). Это утверждение будем доказывать в виде A(k+1) - A(k) = B(k+1) - B(k). Из последнего равенства с учетом того, что A(k) = B(k), получим A(k+1) = B(k+1). A(k+1) - A(k) = (13 + 23 +... + k3 + (k + 1)3) - (13 + 23 +... + k3) = (k+1)3.
B(k+1) - B(k) = П р и м е р 3. Докажите, что при nÎN, n ³ 5 справедливо неравенство 2n ³ n2 + n + 2. Решение Обозначим данное утверждение через M(п). При п = 5 неравенство справедливо: 32 ³ 32. Пусть M(к): 2k ³ k2 + k + 2 при n ³ 5. Докажем, что M(k) Þ M(k+1): 2k+1 ³ (k + 1)2 + (k + 1) + 2, т.е. 2k+1 ³ k2 + 3k + 4. Рассмотрим 2k+1 - k2 - 3k - 4 = 2(2k - k2 - k - 2) + k2 - k ³ 0 на основании индукционного предположения и того, что k2 - k ³ 0 при n ³ 5. На основании принципа математической индукции утверждение М(п) верно при n ³ 5.
П р и м е р 4. Докажите, что при nÎN, n ³ 10 справедливо неравенство 2n > n3. Решение Данное неравенство верно при n = 10. Пусть верно утверждение для некоторого k. Индукционный шаг: 2k+1 > (k + 1)3 Û 2k+1 - k3 - 3k2 - 3k -1 > 0, 2k+1 - k3 - 3k2 - 3k -1 = = 2(2k - k3) + k3 - 3k2 - 3k -1. Остается доказать, что при k ³ 10 k3 - 3k2 - 3k - 1 > 0, что не очевидно. В этом случае индукционное предположение делаем в виде 2k+9 > (k + 9)3. Индукционный шаг: 2k+10 > (k + 10)3 Û 2k+10 - k3 -30k2 - 300k - 1000 > 0. 2k+10 - k3 -30k2 - 300k - 1000 = = 2(2k+9 - k3 - 27k2 - 243k - 729) + (k3 + 24k2 + 186k + 458) > 0.
8.1. Сформулируйте форму математической индукции в которой рассматриваются случаи: 1. n = 1; n и n + 1
2. n = 1; 1 £ к < n и n
3. n = m; m £ n и n + 1
4. n = m; m £ к < n и n
8.2. Докажите, что для любого натурального n. 1. n3 + 5n делится на 6 2. 7 n + 2 + 8 2n + 1 делится на 57. 3. 6 2n + 3 n + 2 + 3 n делится на 11 4. 11 n + 2 + 12 2n + 1 делится на 133 5. 2 5n + 3 + 5n × 3 n + 2 делится на 17. 6. 3 2n + 1 + 5 × 3 2n + 1 делится на19 7. 2 2n + 1 + 3 n + 3 + 1 делится на 11. 8. 3 2n + 1 + 2 n + 2 делится на7. 9. 4 n + 3n - 1 делится на 9. 10. 3 2n + 15 делится на 12 11. 10 n + 18 n -28 делится на 17 12. 7 2n - 4 2n делится на 33. 8.3. Докажите, что для любого натурального n справедливы следующие равентва: 1. 1 + 2 +... + n = 2. 1 2 + 2 2 +... + n 2 = 3. 1 3 + 2 3 +... + n = 4. 1 + 3 + 5 +... + (2n + 1) = (n + 1)2 5. 1 × 2 + 2 × 3 +... + n(n + 1) = 6. 1 × 4 + 2 × 7 +... + n (3n + 1) = n (n + 1)2
7. 1 × 1! + 2 × 2! +... + n × n! = (n + 1)! - 1. 8.
9. sin х + sin 2х +... + sin nx =
10. 1 + сos x + cos 2x +... + cos nx =
8.4. Докажите, что: 1. 2 n > n 2 при n ³ 5, 2. 2 n > 2n + 1 при n ³ 3. 3. 2n < n! при n ³ 4.
З А Н Я Т И Е № 9.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.67.251 (0.05 с.) |
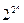 +1. При n = 0, 1, 2, 3, 4 числа f(n) являются простыми. Действительно, f(0) =
+1. При n = 0, 1, 2, 3, 4 числа f(n) являются простыми. Действительно, f(0) = 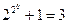 ;
;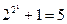 ; f(2) =
; f(2) = 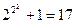 ; f(3) =
; f(3) = 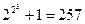
 . Ферма предположил, что все числа такого вида простые. Но через некоторое время Л.Эйлер показал, что уже следующее число f(5) =
. Ферма предположил, что все числа такого вида простые. Но через некоторое время Л.Эйлер показал, что уже следующее число f(5) = 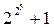 является составным:
является составным: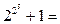 4294967297 = 641. 6700417.
4294967297 = 641. 6700417.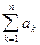 .
.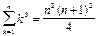 для nÎ N.
для nÎ N.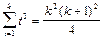 .
.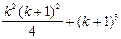 =
= 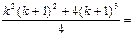
 .
.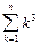 = 13 + 23 + 33 +... + n3; B(n) =
= 13 + 23 + 33 +... + n3; B(n) = 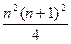 . Надо доказать: ("n Î N) A(n) = B(n)
. Надо доказать: ("n Î N) A(n) = B(n) , т.е. А(1) = В(1).
, т.е. А(1) = В(1).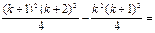
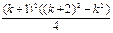 =
= 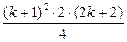 =
= 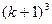 .
.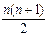


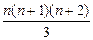
 +
+ 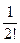 +... +
+... + 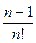 = 1 -
= 1 -