
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Число k-элементных подмножествСодержание книги Поиск на нашем сайте
Конечного множества. Перестановки и сочетания Без повторений
ЗАДАЧА. Сколькими способами можно упорядочить элементы множества А = {a, b, c}? РЕШЕНИЕ. Очевидно, этих способов 6: abc, acb, bac, bca,cab, cba. Это число можно найти и, используя правило произведения: n = 3.2.1 = 3! = 6. (Смотрите также задачу № 68.) Определение. Последовательность, состоящая из всех различных элементов множества, называется его перестановкой. Например, (1; 5; 2; 4; 3) - одна из перестановок множества А = { 1; 2; 3; 4; 5 }. Число различных перестановок множества, состоящего из n элементов, обозначается Рn. Мы видим, что: Рn = n! Найдём все трёхэлементные подмножества множества {a, b, c, d }. Это: {a,b,c}, {a,c, d}, {a,b,d}, {b,c,d}. Итак, число таких подмножеств равно 4. Пусть n(A) = n. Обозначим через r число k-элементных подмножеств множества А. Пусть m - число упорядоченных наборов из k элементов множества А. По правилу произведения m = n.(n -1).....(n - k + 1) Как связаны числа r и m? Очевидно, m = k!.r. Откуда: r = Определение. k-элементные подмножества n-элементного множества А (k £ n) называются сочетаниями без повторений из элементов этого множества по k. Число таких подмножеств обозначается: Сnk. Cnk =
Контрольные вопросы и устные упражнения Свойства операций над множествами. В чем заключается двойственный характер этих свойств? Число элементов объединения множеств. Правило суммы. Упражнения 2.1. Найдите пересечение, объединение, разность множеств А и В, если: 1. А = { 1, 2, 3, 4, 5}, В = {3, 4, 5, 6, 7}; 2. А - множество двузначных чисел, кратных 5 и В - множество двузначных чисел, кратных 3; 3. А = { х | х Î N, х < 37}, В = { х | х Î N, х > 28 }. 2.2. Пусть R - универсальное множество, А = (-1; 3], В = [0; 5). Найдите: 1. А Ç В; 2. А \ В; 3. 6. А È В; 7. В \ А; 8. 2.2. Какие элементы входят в пересечение, объединение множеств букв в словах: 1. математика и грамматика; 2. ворона и сорока; 3. насос и сосна; 4. ветка и роща? 2.3. Изобразите на координатной прямой множества А и В, их пересечение, объединение, разность, а также
2.4. Начертите два треугольника так, чтобы их пересечением: 1) была точка; 2) был отрезок; 3) был треугольник; 4) был четырехугольник.
2.5. Даны множества: А = {15, 17, 18, 21, 29},
В = {12, 17, 21, 37, 43}, С = {18, 21, 29, 43}. Найдите пересечение, объединение, разность множеств А и В, А и С, В и С, а также А Ç (В È С) и А È(В Ç С).
2.6. Какая фигура образуется в пересечении множеств точек {(х, у) | 0 £ у } и {(х, у)| 0 £ х + у £ 5}?
2.7. Дано: А = (0; 1) È [2; ¥), В = [0,5; 3), U = R. Найдите А È В, А Ç В, В \ А, А \ В,
2.8. Дано: А = {1, 2, 3, 4}, В = {3, 4, 5, 6}; C = {1, 3, 5}, U = {1, 2, 3, 4, 5, 6, 7}. Найдите А \ В,
2.9. Докажите следующие свойства: 1. А \ (В È С) = (А \ В) Ç (А \ С) 2. А È (В \ А) = А È В 3. дистрибутивность объединения относительно пере- сечения. 4. дистрибутивность пересечения относительно объединения. 5. А Ç 7. А \ В = 9. А \ В = А Ç
2.10. Докажите равенство множеств при помощи основных свойств операций. 1. (А È В) Ç 3. (А Ç В) È (
2.11. Упростите запись множеств при помощи основных свойств операций. 1 3. (
7.
2.12. Можно ли доказать равенство или включение множеств с помощью диаграмм Эйлера-Венна? Проиллюстрируйте равенство множеств: 1. А Ç (В Ç С) = (А Ç В) Ç С 2. А Ç (В ÈС)= (А ÇВ) È(А ÇС) 3. А È 5. А \ В = А Ç
2.13. Решите уравнения для X Ì И. 1. 5. х È х = х 6. х Ç 8. х Ç (1, 3) = (1, 2) 9. х \ (1, 3) = [1; 2]
2.14. Докажите, что А Ì В. Почему В не будет подмножеством А. 1. А = (\ У) Ç(С \ Д), В = Х Ç С. 2. А = (Х \ У) \ С, В = Х Ç 3. А = Х Ç У, В = (Х È У) \ (Х \ У) 4. А = Х Ç (У \ С), В = (Х È У) \ (Х Ç С).
2.15. Запишите двойственные формулы. Используя свойства операций над множествами, докажите: 1. (А Ç В) È В = В; 2. (А Ç 3..(А Ç В) È (А Ç В) È А = А; 4. (А È В) Ç 5. 6. (А Ç В) È 7. (А Ç В) È (
2.16. Можно ли узнать число участников шахматных соревнований, если в них было: 1. 20 юношей и 12 девушек, 2. 20 юношей и 27 школьников?
2.17 Экзамен по математике сдавали 250 школьников. Оценку ниже 5 получили 180 человек, а выдержали этот экзамен 210 школьников. Сколько человек получили оценки 3 и 4?
2.18. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 -на коньках. Ни на лыжах, ни на коньках не умеют кататься 60 учащихся. Сколько учащихся умеют кататься и на лыжах, и на коньках?
2.19. В группе из 100 туристов 70 человек знают английский язык, 45 знают французский и 23 знают оба языка. Сколько человек не знают ни английского ни французского языка?
2.20. В штучном отделе магазина посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили торт и коробку конфет?
2.21. В отряде из 40 человек 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого. Сколько ребят умеет плавать и играть в шахматы?
2.22. Найдите n А Ç В Ç С), если известно, что n(А)=13, n(В) = 18, n(С) = 9, n(А È В È С) = 40.
2.23. На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги А, В и С. Результаты опроса оказались таковы: книгу А читало 25 учащихся, книгу В - 22, книгу С - также -22. Книгу А или В читали 33 ученика, А или С - 32, В или С 31; все три книги прочитали 10 учащихся. Сколько учеников прочли только по одной книге? Сколько учащихся не читали ни одной из этих трех книг?
2.24. Сколько среди первых 50 натуральных чисел не делятся ни на 2, ни на 3, ни на 5?
2.25. В спортивном лагере 65% ребят умеют играть в футбол, 70% в волейбол, 75% - в баскетбол. Каков наименьшее число ребят, умеющих играть и в футбол, и в волейбол, и в баскетбол?
2.26. Сколько чисел среди первой сотни натуральных не делятся ни на 2, ни на 3, ни на 5, ни на 7?
2.27. Найдите множество решений уравнений: 1.
3. х2 - 7 |х| = 0 4. 2х2 + |х| = 0
5. х2 - 7. х2 + 3 9. х = 3
2.28. Найдите решения неравенств, запишите их в виде промежутков и изобразите на числовой оси: 1. - 2х + 21 > 0; 2. 18 - 3х £ 0;
3.
5. (
7. |х - 2| > 0; 8. |х + 2| £ 3;
9. |5х - 1| ³ - 3; 10. |х - 3| £ -1.
2.29. Найдите область определения функций 1. у =
2. у =
3. у =
2.30. Решите систему неравенств 1.
3. 5.
7.
9. 2.31. Придумайте систему двух неравенств, решением которой является промежуток: 1. (- 3; 0,5]; 2. (- ¥; 1); 3. [ -1; 5 ]; 4. [- 3; + ¥).
2.32. Решите совокупность неравенств: 1. 3. 4. 5. 6. 7.
8. 10.
12.
2.33. Решите неравенства: 1. | х |(3х + 2) > 0; 2. | х-3 |(7х - 4) £ 0; 3. (9х2 + 12х + 4)(3х - 2) ³ 0; 4. (20х - 4х2 - 25)(3х - 8) £ 0; 5. | х2 - 36 | (3 - х) ³ 0; 6. | х2 - 9 | (2х - 3) > 0; 7. 8. З А Н Я Т И Е № 3.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.166.156 (0.011 с.) |

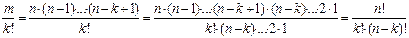
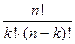
 ; 4.
; 4.  ;
; и
и 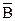 , если А = {х | 2 £ х £ 6}, В = {х | 4 £ х £ 8}.
, если А = {х | 2 £ х £ 6}, В = {х | 4 £ х £ 8}. = И.
= И.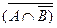 È В 2. ((А È(В È С)) Ç А) È
È В 2. ((А È(В È С)) Ç А) È 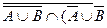 4.
4. 
 5.
5. 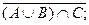 6.
6. 
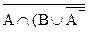 ) È В
) È В 
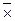 = Æ; 2.
= Æ; 2. 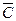
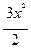 =
=  ; 2.
; 2. 
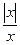 = 0, 6. х2 +
= 0, 6. х2 + 
 8. х2 - 5
8. х2 - 5 
 + 4; 10. х + 5
+ 4; 10. х + 5 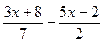 < х; 4.
< х; 4. 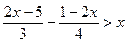 ;
; - 2) х ³ 2
- 2) х ³ 2 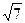 - 3)х < 7 - 3
- 3)х < 7 - 3 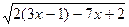


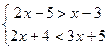 2.
2. 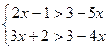
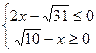 4.
4. 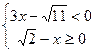
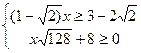 6.
6. 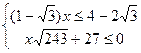
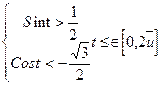 8.
8. 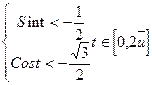
 10.
10. 
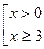 2.
2. 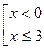
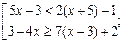
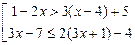
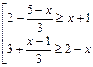 .
.
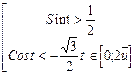
 9.
9. 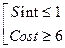
 11.
11. 
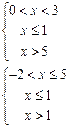 13.
13. 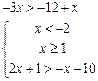

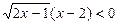 ;
;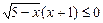 .
.


