
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индексные системы и факторный анализСодержание книги
Поиск на нашем сайте
 ), а объем выпуска продукции – как произведение численности работников на их производительность труда ( ), а объем выпуска продукции – как произведение численности работников на их производительность труда ( ) и т.д.Все сомножители в указанных произведениях могут рассматриваться как факторы, определяющие значение результативного показателя. Например, товарооборот зависит от изменения количества (объема) товаров и от изменения цен. Объем выпуска продукции предприятия зависит от изменения численности работников и от изменения их производительности труда. Поэтому при анализе динамики экономических показателей важно определить роль отдельных факторов в этом изменении. Многие экономические показатели тесно связаны между собой, и образуют так называемые индексные системы. В индексных системах отражается взаимосвязь экономических показателей: если экономические показатели связаны между собой некоторым образом, то таким же образом связаны между собой и характеризующие их индексы, т.е. если ) и т.д.Все сомножители в указанных произведениях могут рассматриваться как факторы, определяющие значение результативного показателя. Например, товарооборот зависит от изменения количества (объема) товаров и от изменения цен. Объем выпуска продукции предприятия зависит от изменения численности работников и от изменения их производительности труда. Поэтому при анализе динамики экономических показателей важно определить роль отдельных факторов в этом изменении. Многие экономические показатели тесно связаны между собой, и образуют так называемые индексные системы. В индексных системах отражается взаимосвязь экономических показателей: если экономические показатели связаны между собой некоторым образом, то таким же образом связаны между собой и характеризующие их индексы, т.е. если  . Например, если товарооборот равен произведению количества проданных товаров на их цену, то и индекс товарооборота равен произведению индекса количества товара на индекс цен ( . Например, если товарооборот равен произведению количества проданных товаров на их цену, то и индекс товарооборота равен произведению индекса количества товара на индекс цен ( . Следует помнить, что изменение цен и изменение физического объема действуют одновременно на результирующий показатель. При этом направление действия этих факторов, их интенсивность, могут быть различными. Для оценки совместного влияния факторов на изменение результативного показателя, используются системы взаимосвязанных индексов (индексные системы).Система взаимосвязанных индексов позволяет использовать индексный метод для изучения взаимосвязи показателей и проведения факторного анализа с целью определения влияния каждого фактора на результативный показатель. Схема проведения факторного анализа: если результативный показатель можно представить в виде произведения количественного (объемного) и качественного факторов, то определяя влияние объемного показателя на результативный, качественный показатель фиксируется на уровне базисного периода; а если определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода. Индексные системы позволяют определить влияние отдельных факторов на формирование уровня результативного показателя, т.е. позволяют по двум известным значениям индексов определить значение неизвестного третьего индекса.Построение индексной системы рассмотрим на примере агрегатного индекса стоимости, индекса цен и индекса физического объема. Индекс стоимости продукции (товарооборота): . Следует помнить, что изменение цен и изменение физического объема действуют одновременно на результирующий показатель. При этом направление действия этих факторов, их интенсивность, могут быть различными. Для оценки совместного влияния факторов на изменение результативного показателя, используются системы взаимосвязанных индексов (индексные системы).Система взаимосвязанных индексов позволяет использовать индексный метод для изучения взаимосвязи показателей и проведения факторного анализа с целью определения влияния каждого фактора на результативный показатель. Схема проведения факторного анализа: если результативный показатель можно представить в виде произведения количественного (объемного) и качественного факторов, то определяя влияние объемного показателя на результативный, качественный показатель фиксируется на уровне базисного периода; а если определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода. Индексные системы позволяют определить влияние отдельных факторов на формирование уровня результативного показателя, т.е. позволяют по двум известным значениям индексов определить значение неизвестного третьего индекса.Построение индексной системы рассмотрим на примере агрегатного индекса стоимости, индекса цен и индекса физического объема. Индекс стоимости продукции (товарооборота):  или или 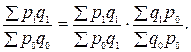 Таким образом, образована индексная система из трех индексов: индекс стоимости продукции Таким образом, образована индексная система из трех индексов: индекс стоимости продукции 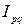 равен произведению индекса цен равен произведению индекса цен  на индекс физического объема продукции на индекс физического объема продукции  . Например, если цена на товары снизилась на 10 %, а физический объем продукции возрос на 6 %. Тогда эти изменения повлияли на стоимость продукции следующим образом: . Например, если цена на товары снизилась на 10 %, а физический объем продукции возрос на 6 %. Тогда эти изменения повлияли на стоимость продукции следующим образом:    ; ;  Таким образом, в результате изменения цены и физического объема продукции, стоимость продукции уменьшилась на 4,6 % (95,4 % - 100 %). Аналогично определяется взаимосвязь других результативных признаков с факторными признаками. Индекс затрат на производство продукции (услуг): Таким образом, в результате изменения цены и физического объема продукции, стоимость продукции уменьшилась на 4,6 % (95,4 % - 100 %). Аналогично определяется взаимосвязь других результативных признаков с факторными признаками. Индекс затрат на производство продукции (услуг):  или или  Таким образом, индекс затрат на производство Таким образом, индекс затрат на производство  равен произведению индекса себестоимости равен произведению индекса себестоимости  и индекса физического объема продукции и индекса физического объема продукции  , т.е. образована индексная система. Индекс изменения объема продукции , т.е. образована индексная система. Индекс изменения объема продукции  в связи с изменением численности работников в связи с изменением численности работников  и уровня их выработки и уровня их выработки  : :  или или  где где  - индекс производительности труда, рассчитываемый по формуле Ласпейреса; - индекс производительности труда, рассчитываемый по формуле Ласпейреса;  - индекс численности работников, рассчитываемый по формуле Пааше.Рассмотренные индексные системы являются двухфакторными (связь результативного признака с двумя факторами). Но результативный признак может зависеть от трех, четырех и более факторов. В этой связи общий индекс можно разложить и на большее число факторов. Соответственно можно получить многофакторные индексные системы, показывающие изменение результативного показателя за счет влияния каждого фактора в отдельности.Таким образом, построение системы взаимосвязанных индексов позволяет одновременно решать две задачи: определять изменение результативного показателя, как в относительном, так и в абсолютном выражении за счет влияния отдельных факторов.Расчеты по определению в абсолютном выражении изменений результативного показателя за счет отдельных факторов, называют разложением абсолютного прироста (убыли) по факторам. Рассмотрим разложение абсолютного прироста (убыли) по факторам для рассмотренной выше индексной системы, согласно которой агрегатный индекс стоимости продукции равен произведению индекса цены на индекс физического объема продукции - индекс численности работников, рассчитываемый по формуле Пааше.Рассмотренные индексные системы являются двухфакторными (связь результативного признака с двумя факторами). Но результативный признак может зависеть от трех, четырех и более факторов. В этой связи общий индекс можно разложить и на большее число факторов. Соответственно можно получить многофакторные индексные системы, показывающие изменение результативного показателя за счет влияния каждого фактора в отдельности.Таким образом, построение системы взаимосвязанных индексов позволяет одновременно решать две задачи: определять изменение результативного показателя, как в относительном, так и в абсолютном выражении за счет влияния отдельных факторов.Расчеты по определению в абсолютном выражении изменений результативного показателя за счет отдельных факторов, называют разложением абсолютного прироста (убыли) по факторам. Рассмотрим разложение абсолютного прироста (убыли) по факторам для рассмотренной выше индексной системы, согласно которой агрегатный индекс стоимости продукции равен произведению индекса цены на индекс физического объема продукции  : : 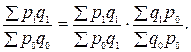  или или  где:
Пример. Имеются следующие данные об объеме продаж и ценах на туры туристской фирмы за 2008 и 2009 гг. (табл. 9.2). Таблица 9.2
Рассчитаем агрегатные индексы количества продукции
Количество проданных туров в 2009 году увеличилось по сравнению с 2008 годом на 6,2 % (106,2 % - 100 %).
Цены по трем направлениям в 2009 году по сравнению с 2008 годом в среднем увеличились на 8,9 %.
Абсолютная экономия покупателей от изменения цен:
Стоимость туров (товарооборот) в текущем периоде по сравнению с базисным увеличилась в среднем на 15, 6 %.
Проверим взаимосвязь между индексами:
Разложение абсолютных приростов по факторам:
830 = 500 + 330, 830 = 830 – верно. Таким образом, метод разложения абсолютных приростов по факторам подтверждает правильность расчетов.
Идеальный индекс Фишера Выбор формулы для оценки динамики средней цены (качественного показателя) зависит от цели исследования и принятой в стране методологии расчета. Теоретически нет ответа на вопрос, какая из формул индекса цены наиболее точно характеризует изменение индексируемой величины. В этой связи, американский экономист И. Фишер предложил использовать среднюю геометрическую из агрегатных индексов цен Пааше и Ласпейреса:
Этот индекс не имеет конкретного экономического содержания: разность числителя и знаменателя не показывает реальной экономии (потерь) из-за изменения цен на продукцию.
Формула Фишера может быть использована и для определения индекса физического объема продукции:
И. Фишер назвал формулу расчета индекса «идеальной», так как индекс обратим во времени. Это означает, что при перестановке базисного и отчетного периодов получается «обратный» индекс (величина, обратная величине исходного индекса). Данному условию удовлетворяет идеальный индекс цен Фишера:
В специальной литературе применение индекса Фишера обосновывается необходимостью устранить эффект Гершенкрона (индекс цен Ласпейреса, как правило, больше индекса цен Пааше). Эффект Гершенкрона наблюдается при отрицательной зависимости между объемом произведенной (реализованной) продукции и ценами. Из-за трудности экономической интерпретации индекс Фишера применяется редко, в основном при расчетах индексов цен за длительный период времени и при территориальных сопоставлениях.
Контрольные вопросы 1. Дайте определение индекса. В чем состоит его практическое значение? 2. В чем состоит классификация экономических индексов? 3. В чем состоят задачи индексов? 4. Какие индексы называются индивидуальными, а какие общими? 5. В каких случаях используются индивидуальные и общие индексы? 6. Назовите две функции общих индексов. 7. Назовите формы общих индексов. 8. В чем суть построения агрегатных индексов? 9. Запишите формулы агрегатных индексов физического объема, товарооборота и цен (Пааше и Ласпейреса). 10. Как определяется абсолютная экономия (перерасход) средств от изменения цен на продукцию. 11. Сформулируйте правило выбора соизмерителей (весов) индекса. 12. Расскажите о способах построения средних индексов. 13. Что характеризуют индексы постоянного, переменного составов и структурных сдвигов. 14. Какие индексы называются цепными, базисными? 15. Какая взаимосвязь существует между цепными и базисными индексами? 16. Что такое индексные системы, и в чем состоит факторный анализ? 17. Что называется разложением абсолютного прироста по факторам? 18. Как рассчитывается индекс Фишера? 19. Расскажите о сфере применения индексов в экономическом анализе.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.247 (0.008 с.) |



 - изменение стоимости продукции в результате изменения цен
- изменение стоимости продукции в результате изменения цен 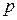 и количества
и количества 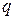 проданных товаров;
проданных товаров;
 - изменение стоимости продукции в результате изменения цен
- изменение стоимости продукции в результате изменения цен 

 - изменение стоимости продукции в результате изменения количества
- изменение стоимости продукции в результате изменения количества  или 106, 2 %.
или 106, 2 %. или 108,9 %.
или 108,9 %. =6140 – 5640=500 тыс. руб. > 0 – перерасход населения от повышения цен, экономии нет.
=6140 – 5640=500 тыс. руб. > 0 – перерасход населения от повышения цен, экономии нет. или 115,6 %.
или 115,6 %. ,
, - верно.
- верно. ,
, ;
; .
.




