
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое изображение вариационных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Анализ рядов распределения предполагает их графическое изображение. Для этой цели строят графики – полигон, гистограмму, кумуляту и огиву распределения. Полигон используется при графическом изображении дискретных вариационных рядов. Для его построения на оси абсцисс откладывают варианты признака хi, а на оси ординат – их частоты fi или частости wi. Полученные на пересечении абсцисс и ординат точки последовательно соединяют и получают ломаную линию, называемую полигоном частот, или эмпирической кривой распределения. Для примера по данным табл. 3.4 представлен полигон распределения туристских фирм по числу сотрудников (рис. 3.2).
Рис 3.2. Полигон распределения Замечание. Полигон часто замыкается. Для этого крайние точки соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе от Гистограмма используется при графическом изображении интервальных вариационных рядов. Для построения гистограммы на оси абсцисс откладывают границы интервалов признака хi, а частоты fi изображаются прямоугольниками, построенными на соответствующих интервалах с высотой в масштабе оси ординат. Высота столбиков должна быть пропорциональна частотам fi или частостям wi. В результате гистограмма представляет собой ряд сомкнутых прямоугольников, основаниями которых служит величина интервалов значений хi, а высотой – частота fi или частость wi. График гистограммы построен по данным табл. 3.5 и представлен на рис. 3.3.

Рис. 3. 3. Гистограмма распределения сотрудников туристского предприятия по стажу работы В случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения Замечание. Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями. Замечание. С помощью гистограммы графически можно определить приближенное значение моды М0. Для этого правую вершину наибольшего прямоугольника соединяют прямой линией с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых является модой распределения. На рис. 3.3 прямые линии, соединяющие вершины прямоугольников, и перпендикуляр из точки их пересечения обозначены пунктирными линиями. Точное значение моды в случае интервального ряда определяется по специальной формуле (см. § 5.3).
В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята). Для ее построения следует рассчитать накопленные частоты или частости. При помощи кумуляты изображается ряд накопленных частот. При этом на оси абсцисс откладываются варианты хi или верхние границы интервалов, а на оси ординат - соответствующие накопленные частоты Fi (или частости wi). В верхних границах интервалов проводят перпендикуляры к оси абсцисс. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумулятивную кривую. Она начинается в точке нижней границы первого интервала (с частотой, равной нулю) и заканчивается в точке, соответствующей общей сумме частот. На основе табл. 3.5 построена кумулята распределения сотрудников туристского предприятия по стажу работы (рис. 3.4).
Рис. 3.4. Кумулята распределения сотрудников туристского предприятия по стажу работы Изображение вариационного ряда в виде кумуляты целесообразно в следующих случаях: 1) при сравнении вариационных рядов; 2) при наблюдении за процессом концентрации изучаемого явления (например, для анализа концентрации производства). Замечание. С помощью кумуляты графически можно найти приближенное значение медианы Mе . Для этого на оси у находят точку Если поменять местами оси координат, то есть, на оси х откладывать накопленные частоты Fi (или частости wi), а на оси y – варианты хi, то построенная на них кумулятивная кривая называется огивой. При оценке степени концентрации (концентрации производства, капитала и др.) используется разновидность кумулятивной кривой – кривая Лоренца. График используется для анализа концентрации признака в тех или иных группах совокупности (для характеристики процессов концентрации, дифференциации и т.д.). При этом рассматривают параллельное изменение нарастающих долей единиц совокупности и нарастающих долей значений признака в общем объеме.
При построении на оси х откладывают накопленные частости (pi) объема совокупности, а на оси у – накопленные частости значений признака (q i) в общем объеме. Наносятся точки в соответствии с накопленными значениями двух рядов. Соединив точки, получают кривую, характеризующую степень неравномерности распределения. Если распределение является строго равномерным, то первые 10 % единиц обладают 10 % объема признака, первые 20 % единиц - соответственно 20 % объема признака и т.д. Это распределение отображается прямой, соединяющей нижний левый угол графика с правым верхним углом (диагональ четырехугольника), и называется линией равномерного распределения. Чем сильнее концентрация изучаемого признака (чем больше фактическое распределение двух показателей отклоняется от равномерного), тем больше кривая Лоренца отклоняется от линии равномерного распределения и наоборот. На рис. 3.5 представлена кривая Лоренца распределения выручки по предприятиям региона (см. графы 6 и 9 табл. 3.6).
Рис. 3.5. Кривая Лоренца для распределения выручки туристских предприятий Значит, чем больше это удаление (вогнутость), тем выше концентрация изучаемого показателя (в нашем случае – величины выручки) в определенных группах единиц (в нашем случае – в крупных предприятиях). Кривая степени концентрации может сколько угодно приближаться к линии равномерного распределения, но никогда ее не пересечет. Для количественного измерения степени концентрации определенного суммарного показателя по выделенным группам единиц совокупности применяются следующие показатели: § коэффициент Джини; § коэффициент Лоренца; § коэффициент Герфиндаля. Статистические таблицы Результаты сводки и группировки материалов статистического наблюдения, как правило, оформляются в виде статистических таблиц. Статистическая таблица – это таблица, содержащая сводную количественную характеристику изучаемой совокупности по одному или нескольким существенным признакам. Таблица является наиболее рациональной, наглядной и компактной формой представления статистического материала. Применение статистических таблиц позволяет определить размеры, структуру и динамику изучаемых явлений. При построении статистических таблиц необходимо исходить из целей статистического исследования и содержания полученного материала. Замечание. Статистическая таблица отличается от других табличных форм тем, что: 1) содержит результаты подсчета эмпирических данных; 2) является итогом сводки. Статистическая таблица представляет собой пересечение горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали — графы (столбцы, колонки). Строки и графы формируют остов (основу) статистической таблицы. Незаполненная цифрами статистическая таблица называется макетом. Макеты статистических таблиц разрабатывают на стадии подготовки к этапу сводки и группировки статистических данных. Содержание статистической таблицы выражают ее основные элементы - подлежащее и сказуемое. Составленная и оформленная статистическая таблица должна иметь общий, боковые и верхние заголовки (схема 1).
Название таблицы (общий заголовок)
Схема 1. Основные элементы статистической таблицы Подлежащим таблицы называется объект изучения (единицы статистической совокупности или их группы), характеризующийся цифрами. Сказуемое таблицы – это показатели, характеризующие подлежащее. Обычно подлежащее таблицы дается в левой части и составляет наименование ее строк, а сказуемое – в верхней части в виде наименования граф. В таблице могут быть подведены итоги по графам и строкам. Иногда в целях получения более компактной таблицы подлежащее и сказуемое меняют местами, т.е. подлежащее указывают по графам, а сказуемое — по строкам. Подлежащее статистической таблицы может быть простым и сложным. По характеру подлежащего различают три вида таблиц: простые, групповые и комбинационные. В простой таблице подлежащее представляет собой перечень: § отдельных единиц совокупности (перечневые таблицы), или одна какая-либо единица выделена по определенному признаку (монографические таблицы);
В подлежащем простой таблицы нет группировки единиц совокупности. Простые таблицы дают справочный материал. Как правило, отражают наличие и распределение ресурсов в стране и регионах, характеризуют динамику тех или иных показателей. Пример. Простая таблица (табл. 3.7 – 3.8). Таблица 3.7
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.96.135 (0.01 с.) |


 и
и 
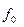 или
или  , так как в этом случае именно плотность дает представление о заполненности каждого интервала.
, так как в этом случае именно плотность дает представление о заполненности каждого интервала.
 . Через нее проводят прямую, параллельную оси х, до пересечения с кумулятой. Абсцисса точки пересечения является медианой. На рис. 3.4 показаны пунктирные линии, определяющие медиану. Точное значение медианы в случае интервального вариационного ряда определяется по специальной формуле (см. §. 5.3).
. Через нее проводят прямую, параллельную оси х, до пересечения с кумулятой. Абсцисса точки пересечения является медианой. На рис. 3.4 показаны пунктирные линии, определяющие медиану. Точное значение медианы в случае интервального вариационного ряда определяется по специальной формуле (см. §. 5.3).



