
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурные средние величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для характеристики среднего значения признака в вариационном ряду применяются показатели центра распределения: средняя величина Структурные средние (мода, медиана) применяются для изучения внутреннего строения, структуры совокупности. В отличие от средней арифметической, на которую оказывают влияние все значения признака Мода ( Мода широко используется в коммерческой практике при изучении покупательского спроса, регистрации цен и т.д. Мода обладает определенной устойчивостью к вариации признака. Поэтому ее наиболее удобно применять при изучении рядов с неопределенными границами. При расчете моды следует учитывать, что она по-разному определяется в дискретных и интервальных вариационных рядах. В дискретном ряду модой является вариант с наибольшей частотой (частостью). В интервальном вариационном ряду с равными интервалами для расчета моды сначала определяют модальный интервал (интервал, имеющий наибольшую частоту или частость), а затем применяют формулу:
В интервальном ряду моду можно определить графически по гистограмме (см. § 3.5). Для ряда с неравными интервалами модальный интервал определяется по наибольшей плотности распределения Медиана ( Таким образом, медианой является значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности: половина единиц совокупности имеют значения признака, меньше, чем медиана, а половина – больше. Медиана используется при статистическом контроле качества продукции, при изучении распределения семей по величине дохода и др. Ранжированный ряд – это ряд, построенный в порядке возрастания или убывания индивидуальных значений признака. В этой связи можно сказать, что медиана лежит в середине ранжированного ряда и делит его пополам. Также как и мода, медиана не зависит от крайних значений признака, и поэтому применяется для характеристики центра в ряду распределения с неопределенными границами. В этой связи медиана является лучшей характеристикой центральной тенденции в следующих случаях: 1) границы крайних интервалов открыты; 2) в ряду имеются чрезмерно большие или малые значения признака; 3) имеют место резкие различия между максимальным и минимальным значениями признака. Из этого следует, что медиана практически выполняет функции средней для неоднородной совокупности. Расчет медианы имеет свою специфику. Способ расчета зависит от вида ряда распределения (дискретный или интервальный) и от объема совокупности (четный или нечетный). Положение медианы в ранжированном ряду определяется ее номером:
В дискретном вариационном ряду с нечетным числом единиц ( Пример 5.4. Рассчитать значение медианы по данным о стаже работы 11 –ти сотрудников предприятия: 7, 7, 5, 3, 3, 2, 4, 5, 6, 2, 2 (лет). Решение. Строим ранжированный ряд:
Число единиц равно 11 (нечетно). Находим номер медианы: В дискретном вариационном ряду с четным числом единиц ( Пример 5.5. Рассмотрим порядок вычисления медианы в случае четного числа индивидуальных значений. Допустим, число сотрудников равно не 11, а 12 человек: 7, 7, 5, 3, 3, 2, 4, 5, 6, 2, 2, 6 (лет). Тогда ранжированный ряд будет выглядеть следующим образом (добавляем одно значение, равное 6):
Порядковый номер медианы:
Это означает, что медиана расположена между шестым и седьмым значениями признака в ранжированном ряду, который содержит четное число единиц. В этом случае медиана равна средней арифметической из соседних значений: 4 и 5.
В интервальном вариационном ряду сначала указывают интервал, в котором находится медиана. Медианный интервал – это первый интервал, в котором сумма накопленных частот Численное значение медианы определяется по формуле:
где:
В интервальном ряду медиану можно определить графически по кумуляте (см. § 3.5). Пример 5.6. По данным табл. 3.4. рассчитать средний стаж работы Решение. Ряд распределения является интервальным. Поэтому переходят к серединам соответствующих интервалов:
Таблица 5.3 Распределение сотрудников туристского предприятия по стажу работы
Cредняя арифметическая Для нахождения моды сначала определяется модальный интервал:
При нахождении медианы сначала определяют накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот В нашем случае медианным является интервал с границами 6-9. Теперь рассчитаем медиану:
Следует заметить, что расчет модального и медианного значений для вариационных рядов с неравными интервалами осуществляется по аналогичным формулам. Для сопоставимости неравных интервалов вместо показателей частот (частостей) используются показатели абсолютной Медиана находит свое практическое применение вследствие особого свойства – сумма абсолютных отклонений членов ряда от медианы есть величина наименьшая, т.е. Таким образом, в соответствии с вышеизложенным, приходим к выводу: § средняя арифметическая § мода М0 - это величина, вокруг которой группируется наибольшее количество единиц совокупности. § медиана Ме - отражает значение признака, сумма отклонений от которого является наименьшей величиной. Соотношение моды М0, медианы Ме и средней арифметической Рассмотрим возможные случаи соотношения моды, медианы и средней величины, определяющие характер распределения: 1. х = Me = Mo - симметричное распределение; 2. 3. Мо < Ме < Симметричное распределение –это распределение, в котором частоты двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. При левосторонней асимметрии большая часть единиц совокупности имеет значения признака ниже модального. На графике распределения левая ветвь вытянута больше, чем правая. При правостороннейасимметрии большая часть единиц совокупности имеет значения изучаемого признака, превышающие модальное значение. На графике распределения правая ветвь относительно максимальной ординаты вытянута больше, чем левая. Нашему примеру соответствует соотношение Чем больше расхождение между средней арифметической и модой, тем более асимметричен ряд. Для умеренно ассиметричных рядов разность между модой и средней примерно в три раза превышает разность между медианой и средней:
В нашем случае, При анализе вариационного ряда важно знать не только направление асимметрии (правосторонняя или левосторонняя), но и ее степень, которая измеряется с помощью коэффициента асимметрии.
Контрольные вопросы 1. Дайте определение средней величины. 2. Каково значение средних величин в статистике? 3. Перечислите условия и задачи применения средних величин. 4. Назовите категории средних величин. 5. В чем состоит отличие простой средней от взвешенной? 6. Приведите формулы расчета степенных средних величин. 7. Сформулируйте правило мажорантности средних. 8. В чем состоит особенность расчета средних величин в интервальных рядах? 9. Назовите сферу применения степенных средних величин. 10. Перечислите свойства средней арифметической величины. 11. В чем состоит применение метода моментов при расчете средних величин? 12. Дайте определение и назовите сферу применения структурных средних величин. 13. В чем состоит специфика расчета структурных средних величин в дискретных и интервальных рядах распределения? 14. Перечислите возможные случаи соотношения моды, медианы и средней величины, определяющие характер распределения.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.011 с.) |

 , мода
, мода 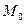 и медиана
и медиана 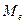 . Средняя величина характеризует типичный уровень признака в совокупности.
. Средняя величина характеризует типичный уровень признака в совокупности.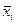 , структурные средние: не зависят от крайних значений признака; выступают как конкретные величины; совпадают с вполне определенными вариантами совокупности. Поэтому, когда для характеристики совокупности расчет средних степенных невозможен, применяются структурные средние величины.
, структурные средние: не зависят от крайних значений признака; выступают как конкретные величины; совпадают с вполне определенными вариантами совокупности. Поэтому, когда для характеристики совокупности расчет средних степенных невозможен, применяются структурные средние величины. , где:
, где: нижняя граница модального интервала;
нижняя граница модального интервала;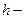 величина модального интервала;
величина модального интервала;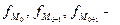 частоты (частости)соответственно модального, предыдущего и последующего интервалов.
частоты (частости)соответственно модального, предыдущего и последующего интервалов.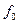 или
или  . Это объясняется тем, что моду можно рассматривать как значение признака, которому соответствует максимальная плотность распределения.
. Это объясняется тем, что моду можно рассматривать как значение признака, которому соответствует максимальная плотность распределения.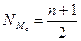 , где n – число единиц совокупности. Затем по накопленным частотам
, где n – число единиц совокупности. Затем по накопленным частотам  определяют ее численное значение.
определяют ее численное значение.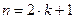 ) медианной является срединное значение ранжированного ряда.
) медианной является срединное значение ранжированного ряда.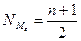 =
=  . На шестом месте стоит х6=4, который и является медианной:
. На шестом месте стоит х6=4, который и является медианной: 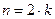 ) медианной также является срединное значение ранжированного ряда. Вначале определяют ее место
) медианной также является срединное значение ранжированного ряда. Вначале определяют ее место 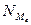 , а затем - находят как среднюю из двух центральных значений по формуле:
, а затем - находят как среднюю из двух центральных значений по формуле:  .
.
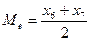 =
= 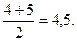
 , т.е.
, т.е.  . Для его определения необходимо подсчитать сумму накопленных частот (частостей) до числа, превышающего половину объема совокупности.
. Для его определения необходимо подсчитать сумму накопленных частот (частостей) до числа, превышающего половину объема совокупности.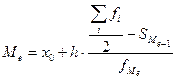 ,
,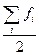 - половина объема совокупности;
- половина объема совокупности;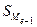 - сумма накопленных частот, предшествующих медианному интервалу;
- сумма накопленных частот, предшествующих медианному интервалу; - частота медианного интервала.
- частота медианного интервала.
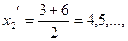
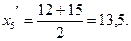

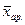 =
= 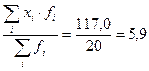 лет.
лет.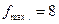 , следовательно, модальным является интервал от 6 до 9 лет.
, следовательно, модальным является интервал от 6 до 9 лет.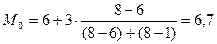 лет - наиболее часто встречающийся стаж сотрудников.
лет - наиболее часто встречающийся стаж сотрудников. >
> 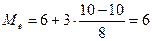 лет – половина сотрудников имеет стаж до 6 лет, а половина – более 6 лет.
лет – половина сотрудников имеет стаж до 6 лет, а половина – более 6 лет. Это свойство медианы находит широкое применение в маркетинговой деятельности.
Это свойство медианы находит широкое применение в маркетинговой деятельности.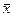 - часто используется в качестве показателя центра распределения, положительные и отрицательные отклонения от которого индивидуальных значений признака в сумме взаимно погашаются;
- часто используется в качестве показателя центра распределения, положительные и отрицательные отклонения от которого индивидуальных значений признака в сумме взаимно погашаются; .
. что свидетельствует о сильной асимметрии.
что свидетельствует о сильной асимметрии.


