
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурные средние величины.Содержание книги Поиск на нашем сайте
К структурным средним величинам относятся: 1) Мода (Мо) 2) Медиана (Ме) 3) Квартили (Q) 4) Децили (D) Все средние структурные являются именованными величинами и выражаются в тех же единицах измерения, что и значения признака (варианты). 1. Модей в статистике называют значение признака (вариант), который наиболее часто встречается в исходной совокупности. В дискретном вариационном ряду Мо является вариант, имеющий наибольшую частоту. Рассмотрим на примере с семьями:
В этом примере наибольшей частоте 8 соответствует значение признака – 1 ребенок, это и есть значение Мо и, следовательно, наиболее часто встречаются в данном примере семьи, имеющие одного ребенка. В интервальном вариационном ряду с равными интервалами по наибольшей частоте (частости) находят интервал, содержащий Мо (модальный интервал) и далее Мо вычисляют по формуле:
В этом примере наибольшая частота равна 30, следовательно, Мо содержится в интервале от 50 до 59 лет. В интервальном вариационном ряду Мо можно также вычислить графически по гистограмме:
В интервальном вариационном ряду с неравными интервалами для определения Мо необходимо: 1. рассчитать частости W 2. вычислить плотность распределения путем деления частости на величину соответствующего интервала: Z=W/i. 3. по наибольшей плотности распределения найти модальный интервал 4. Мо вычислить по формуле: В интервальном вариационном ряду с неравными интервалами Мо можно вычислить графически по гистограмме. Для этого по оси ординат вместо частот откладываются соответствующие плотности распределения.
Лекция № 5 Медиана – это значение признака при котором исходная совокупность делится на 2 равные части, при этом первая половина совокупности имеет значение признака меньше, чем медиана, а вторая имеет значения признака больше, чем медиана. Квартиль делит исходную совокупность на 4 равные части. На практике вычисляют первый (нижний) квартиль, который делит исходную совокупность в соотношении ¼: ¾ и третий (верхний) квартиль, который делит исходную совокупность в соотношении ¾: ¼. Дециль делит исходную совокупность на 10 равных частей. Например: второй D делит исходную совокупность в соотношении 2/10: 8/10; девятый D делит исходную совокупность в соотношении 9/10: 1/10. В дискретном вариационном ряду для определения Ме, квартилей и децилей необходимо: 1) Вычислить накопленные частоты. 2) Определить порядковый номер единицы, которая делит исходную совокупность в нужном нам соотношении. Например: для Ме: 3) По накопленным частотам найти значение признака, которое имеет нужная нам единица совокупности. Пример (про семьи):
По накопленным частотам определяем, что 10-ой единице совокупности (10-ой семье) соответствует значение признака равное 1, значит Ме равна 1 ребенку. Половина семей имеют 1 ребенка и вообще не имеют детей, а вторая половина имеют 1 ребенка и больше.
В интервальном вариационном ряду для определения медианы, квартилей и децилей необходимо: 1) Вычислить накопленные частоты. 2) Найти порядковый номер единицы, которая делит исходную совокупность в нужном нам соотношении. 3) По накопленным частотам найти интервал, содержащий нужную нам единицу совокупности. 4) Медиану, квартили и децили вычисляют по формулам:
В интервальном вариационном ряду медиану можно вычислить графически по кумуляте:
Квартиль вычисляют по формуле: Дециль вычисляют по формуле: В интервальном вариационном ряду квартиль и дециль можно вычислить графически по кумуляте:
Изменение величины признака от одной единицы совокупности к другой в статистике называют вариацией признака. Кроме средних величин для анализа исходной совокупности вычисляют абсолютные и относительные показатели вариации. К абсолютным показателям относятся: 1) Размах вариации (R) определяется, как разность между максимальным и минимальным значением признака в исходной совокупности R=Xmax-Xmin. 2) Среднее квартильное отклонение. Определяется как половина разности 3-его и 1-ого квартиля: 3) Среднее линейное отклонение (d). Определяется, как средняя арифметическая величина из абсолютных отклонений индивидуальных значений признака от их средней величины. Применяют 2 формулы для не сгруппированных данных и сгруппированных. Для не сгруппированных: 4) Дисперсия ( Для не сгруппированных: 5) Среднее квадратическое отклонение представляет собой квадратный корень из дисперсии. Для не сгруппированных: Среднее квадратическое отклонение показывает на сколько в среднем отличаются индивидуальные значения признака (варианты) в исходной совокупности от средней величины. Показатель среднего квадратического отклонения применяется при оценке возможного риска в финансово-экономических расчетах. Лекция №6. К относительным показателям вариации относятся: 1. Коэффициент квартильной вариации, который вычисляется по формуле:
2. Коэффициент осцилляции: 3. Коэффициент вариации: исходная совокупность считается однородной по изучаемому признаку, если коэффициент вариации меньше 33%. В этом случае средняя величина объективно представляет свою исходную совокупность. Пример вычисления показателей вариации:
В среднем возраст каждого депутата отличается от среднего возраста для депутатов данной фракции на 9,2 лет. Данная совокупность депутатов считается однородной по возрасту, т. к. коэффициент вариации меньше 33%.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1182; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.208.243 (0.007 с.) |

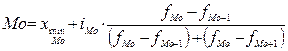 , где:
, где: 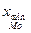 - нижняя граница интервала, содержащая Мо; iMo – величина модального интервала; fMo – частота модального интервала;
- нижняя граница интервала, содержащая Мо; iMo – величина модального интервала; fMo – частота модального интервала;  - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; 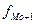 - частота интервала, следующего за модальным. Пример:
- частота интервала, следующего за модальным. Пример: Таким образом вычислили, что наиболее часто встречаются депутаты в возрасте 50,7 лет.
Таким образом вычислили, что наиболее часто встречаются депутаты в возрасте 50,7 лет.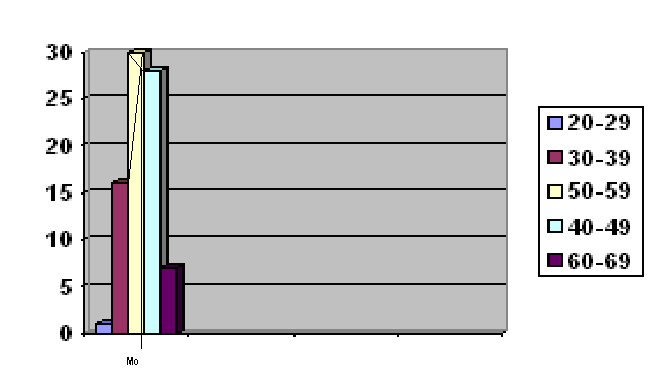

 ; для первого Q:
; для первого Q:  ; для девятого D:
; для девятого D:  .
.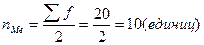
 ;
;  Таким образом мы вычислили, что ¾ семей (75%) имеют 2-ух детей и меньше, а 25% семей имеют более 2-ух детей; 90% семей имеют 3-ех детей и меньше, а 10% более 3-ех детей.
Таким образом мы вычислили, что ¾ семей (75%) имеют 2-ух детей и меньше, а 25% семей имеют более 2-ух детей; 90% семей имеют 3-ех детей и меньше, а 10% более 3-ех детей.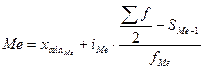 , где
, где 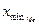 - нижняя граница медианного интервала (интервала, содержащего единицу, которая делит всю совокупность на 2 равные части);
- нижняя граница медианного интервала (интервала, содержащего единицу, которая делит всю совокупность на 2 равные части); 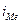 - величина медианного интервала;
- величина медианного интервала;  - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному; 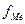 - частота медианного интервала. Пример:
- частота медианного интервала. Пример: По накопленным частотам определяем, что 41-ая единица совокупности содержится в интервале 40-49 лет. Этот интервал является медианным.
По накопленным частотам определяем, что 41-ая единица совокупности содержится в интервале 40-49 лет. Этот интервал является медианным.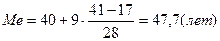 Половина депутатов фракции «Единство» моложе 47,7 лет, 2-ая половина старше 47,7 лет.
Половина депутатов фракции «Единство» моложе 47,7 лет, 2-ая половина старше 47,7 лет.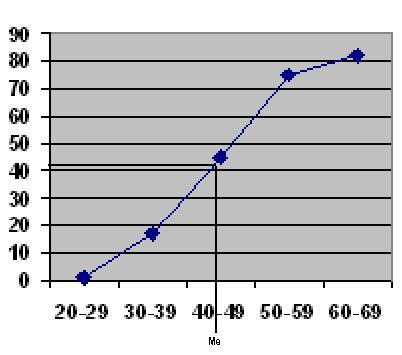
 ;
; 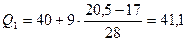

 .
.
 .
. ; для сгруппированных:
; для сгруппированных:  .
. ). Определяется, как средняя арифметическая величина из квадратов отклонений индивидуальных значений признака от из средней величины.
). Определяется, как средняя арифметическая величина из квадратов отклонений индивидуальных значений признака от из средней величины. ; для сгруппированных:
; для сгруппированных:  .
. ; для сгруппированных:
; для сгруппированных: 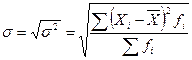 .
.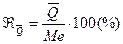
 .
.



 ; R=69-20=49 (лет);
; R=69-20=49 (лет); 
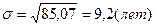 ;
;


