
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические свойства дисперсии.Содержание книги Поиск на нашем сайте
1. Дисперсия, рассчитанная по отношению к средней величине, является минимальной. 2. Дисперсия постоянной величины равна 0. 3. Если все значения признака (варианты) увеличить (уменьшить) на какое-то постоянное число А, то дисперсия новой совокупности не изменится. 4. Если все значения признака (варианты) увеличить (умножить) в К раз, где К – постоянное число, то дисперсия новой совокупности увеличится (уменьшится) в К2 раз. 5. Если вычислена дисперсия по отношению к числу В, отличному от средней величины, то дисперсию исходной совокупности можно рассчитать по формуле: 6. Дисперсию исходной совокупности можно рассчитать как разность между средней квадратов признака и квадратом средней величины.
Расчет дисперсии способом моментов.
В этом случае дисперсия рассчитывается по формуле А=24,5; i=10;
Расчет дисперсии методом средних. Этот способ расчета основан на использовании последнего свойства дисперсии.
Правила сложения дисперсии. Если исходная совокупность разделена на группы по какому-то существенному признаку, то вычисляют следующие виды дисперсий: 1) Общую дисперсию исходной совокупности по формуле: 2) Внутригрупповые дисперсии по формуле: 3) Межгрупповую дисперсию по формуле: Дисперсия альтернативного признака. Наряду с изучением вариаций количественных признаков определяют вариацию альтернативных признаков. Обозначим через p долю единиц совокупности, обладающих альтернативным признаком; через q – долю единиц совокупности не обладающих альтернативны признаком. p+q=1 Наличие признака у единиц совокупности обозначается цифрой 1, отсутствие признака – 0. Вычислим среднюю величину альтернативного признака:
Лекция №7 Выборочное наблюдение. Выборочным называют не сплошное наблюдение, при котором обследованию и изучению подвергаются не все единицы исходной совокупности, а только часть единиц, при этом результат обследования части совокупности распространяется на всю исходную совокупность. Совокупность, из которой производится отбор единиц для дальнейшего обследования и изучения называется генеральной и все показатели, характеризующие эту совокупность, называются генеральными. Средняя величина признака в генеральной совокупности обозначается через Совокупность отобранных единиц называется выборочной и все показатели, характеризующие эту совокупность, называются выборочными. Средняя величина признака в выборочной совокупности обозначается через Возможные пределы отклонений выборочной средней величины от генеральной средней величины называют ошибкой выборки. Чем больше ошибка выборки, тем в большей степени выборочные показатели отличаются от генеральных. Задача выборочного наблюдения состоит в том, чтобы на основе данных выборочной совокупности дать верное представление о генеральной совокупности, т. е. необходимо максимально приблизить выборочные показатели к генеральным и знать возможный предел отклонений этих величин. При прочих равных условиях чем больше численность единиц выборочной совокупности, тем меньше величина ошибки выборки. Средняя ошибка выборки обозначатся буквой Так как средняя ошибка выборки характеризует среднюю величину возможных отклонений выборочных показателей от генеральных, то всегда найдутся единицы генеральной совокупности, которые будут выходить за возможные пределы, такие, как Если мы увеличим возможные пределы отклонений выборочных показателей от генеральных, то с большей вероятностью сможем утверждать, чтот показатели генеральной совокупности отличаются от выборочных показателей не более чем на какую-нибудь величину, которую называют предельной ошибкой выборки. Предельная ошибка выборки обозначается буквой
Таблица для справки:
По способу отбора единиц в выборочную совокупность различают следующие виды выборочного наблюдения (выборки):
По методу отбора единиц в выборочную совокупность различают повторный и бесповторный отбор. При повторном отборе обследованная единица после изучения вновь возвращается в генеральную совокупность и не исключена возможность дальнейшего отбора этой единицы в выборочную совокупность. При бесповторном отборе обследованная единица не возвращается в генеральную совокупность и не участвует в дальнейшем отборе единиц в выборочную совокупность. 1) Собственно-случайная выборка заключается в том, что отбор единиц в выборочную совокупность производится без определенной системности, например, методом жеребьевки. При этом каждая единица генеральной совокупности имеет одинаковую вероятность быть отобранной в выборочную совокупность. Средняя ошибка выборки рассчитывается по формулам: Для повторного отбора: 2) Механическая выборка является разновидностью собственно-случайной выборки и заключается в том, что вся генеральная совокупность разбивается на определенное количество равных частей и затем из каждой части случайным образом производится отбор единиц в выборочную совокупность. Для определения средней ошибки выборки применяют те же формулы, что и при собственно-случайной выборке. 3) Типическая выборка проводится в тех случаях, когда вся генеральная совокупность разбивается на качественно-однородные группы и затем из каждой группы, случайным или механическим образом производится отбор единиц в выборочную совокупность. Формула для повторного отбора: 4) Серийная выборка состоит в том, что обследованию подвергаются не отдельные единицы совокупности, а целые группы или серии единиц. При этом, в данной группе обследованию подвергаются все единицы. Средняя ошибка выборки определяется по формулам: Для повторного отбора: Для определения необходимой численности единиц в выборочной совокупности используют формулы, применяемые для расчета средней ошибки выборки. Лекция №8. Ряды динамики. Одной из задач статистики является изучение изменения социально-экономических явлений и процессов во времени. Эта задача решается с помощью составления и анализа рядов динамики. Ряд динамики представляет собой последовательность числовых значений изучаемого статистического показателя за определенные периоды времени. Числовые значения, составляющие ряд динамики называются уровнями ряда и обозначаются yi (i=1,2,…,n). В зависимости от вида показателей, составляющих ряд динамики, различают ряды абсолютных, относительных и средних величин. Уровни ряда динамики могут относиться к определенным моментам или периодам времени. В зависимости от этого ряды динамики подразделяются на моментные и интервальные. Моментным называют ряд динамики, уровни которого характеризуют величину изучаемого показателя на определенный момент времени (на конкретную дату). Например: приводится численность населения Российской Федерации (млн. чел.): на 01.01.1999 – 146,3; на 01.01.2000 – 145,6; на 01.01.2001 – 144,8; на 01.01.2002 – 144,0; на 01.01.2003 -145,2. Интервальным называют ряд динамики, уровни которого характеризуют величину изучаемого показателя за определенный период времени. Например: приводится объем кредитных вложений в экономику страны: 2000 г. – 808; 2001 г. – 1286; 2002 г. – 1755.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.142.42 (0.007 с.) |

 .
.

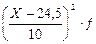
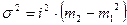 , где i – величина равного интервала или любое постоянное число, отличное от 0; m1- момент первого порядка, m2 – момент второго порядка, который рассчитывается по формуле:
, где i – величина равного интервала или любое постоянное число, отличное от 0; m1- момент первого порядка, m2 – момент второго порядка, который рассчитывается по формуле: 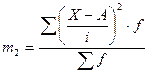 .
. ;
; 
 ;
; 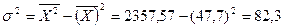
 , где
, где  - общая средняя величина исходной совокупности; f – частоты исходной совокупности. Общая дисперсия характеризует отклонение индивидуальных значений признака от общей средней величины исходной совокупности.
- общая средняя величина исходной совокупности; f – частоты исходной совокупности. Общая дисперсия характеризует отклонение индивидуальных значений признака от общей средней величины исходной совокупности. , где j - номер группы;
, где j - номер группы;  - средняя величина в каждой j-ой группе;
- средняя величина в каждой j-ой группе;  - частоты j-ой группы. Внутригрупповые дисперсии характеризуют отклонение индивидуального значения признака в каждой группе от групповой средней величины. Из всех внутригрупповых дисперсий вычисляют среднюю по формуле:
- частоты j-ой группы. Внутригрупповые дисперсии характеризуют отклонение индивидуального значения признака в каждой группе от групповой средней величины. Из всех внутригрупповых дисперсий вычисляют среднюю по формуле:  , где
, где  - численность единиц в каждой j-ой группе.
- численность единиц в каждой j-ой группе.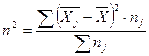 . Межгрупповая дисперсия характеризует отклонение групповых средних величин от общей средней величины исходной совокупности. Правило сложения дисперсий заключается в том. что общая дисперсия исходной совокупности должна быть равна сумме межгрупповой и средней из внутригрупповых дисперсий:
. Межгрупповая дисперсия характеризует отклонение групповых средних величин от общей средней величины исходной совокупности. Правило сложения дисперсий заключается в том. что общая дисперсия исходной совокупности должна быть равна сумме межгрупповой и средней из внутригрупповых дисперсий: 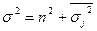 . Результат отношения межгрупповой к общей дисперсии исходной совокупности называется эмпирическим коэффициентом детерминации. Он показывает долю вариации изучаемого признака, обусловленную вариацией группировочного признака.
. Результат отношения межгрупповой к общей дисперсии исходной совокупности называется эмпирическим коэффициентом детерминации. Он показывает долю вариации изучаемого признака, обусловленную вариацией группировочного признака.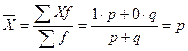 . Средняя величина альтернативного признака равна доле единиц совокупности, обладающих этим альтернативным признаком. вычислим дисперсию альтернативного признака:
. Средняя величина альтернативного признака равна доле единиц совокупности, обладающих этим альтернативным признаком. вычислим дисперсию альтернативного признака:  . Дисперсия альтернативного признака равна произведению доли единиц совокупности, обладающих этим признаком и доли единиц совокупности не обладающих данным признаком.
. Дисперсия альтернативного признака равна произведению доли единиц совокупности, обладающих этим признаком и доли единиц совокупности не обладающих данным признаком.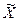 , а численность единиц выборочной совокупности обозначается через n.
, а численность единиц выборочной совокупности обозначается через n. и характеризует среднюю величину отклонений выборочных показателей от генеральных и при этом должно соблюдаться следующее соотношение:
и характеризует среднюю величину отклонений выборочных показателей от генеральных и при этом должно соблюдаться следующее соотношение:  .
. и
и  .
. и вычисляется по формуле
и вычисляется по формуле  , где
, где  .
. ; для бесповторного отбора:
; для бесповторного отбора:  ; где
; где 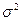 - дисперсия выборочной совокупности.
- дисперсия выборочной совокупности. ; для бесповторного отбора:
; для бесповторного отбора: 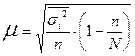 ; где
; где  - средняя из внутригрупповых дисперсий.
- средняя из внутригрупповых дисперсий. ; для бесповторного отбора:
; для бесповторного отбора:  ; где
; где 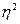 - межгрупповая дисперсия; r – количество групп или серий в выборочной совокупности; R – количество групп или серий в генеральной совокупности.
- межгрупповая дисперсия; r – количество групп или серий в выборочной совокупности; R – количество групп или серий в генеральной совокупности.


