Абсолютные и относительные величины.

В результате проведения статистического наблюдения мы получаем первичные данные, которые характеризуют объект нашего исследования. Такие первичные данные называют абсолютными величинами. Абсолютная величина – это количественный показатель, выражающий общую численность, размеры. Уровни и другие характеристики изучаемого объекта. Абсолютные величины могут быть выражены в натуральных, стоймостных и трудовых единицах измерения. В зависимости от того, какую часть исходной совокупности они характеризуют, абсолютные величины подразделяют на индивидуальные, групповые и свободные (совокупные). Результат отношения двух абсолютных величин статистики называют относительной величиной. Различают 7 видов относительных величин:

1. Относительная величина плана (прогноза). Определяется, как отношение планового показателя текущего (отчетного периода) к фактическому показателю предшествующего (базисного) периода и показывает во сколько раз планом предусмотрено изменение изучаемых показателей в текущем периоде по сравнению с предшествующим.

2. Относительная величина выполнения плана. Определяется, как отношение фактического показателя текущего (отчетного) периода к плановому показателю этого же периода и показывает, во сколько раз изучаемый показатель текущего периода изменился по сравнению с планом.

3. Относительная величина динамики. Характеризует изменение изучаемого показателя во времени и определяется как отношение фактического показателя текущего периода к фактическому показателю предшествующего периода.

Между этими тремя перечисленными относительными величинами существует определенная взаимосвязь. Относительная величина динамики должна быть равна произведению относительной величины плана и относительной величины выполнения плана. (ОВд. = ОВпл.* ОВвпл.) Пример: в 2002 году фирмой было выпущено 200 тыс. штук телевизоров, а на 2003 год запланирован выпуск 260 тыс. штук телевизоров. Фактически в 2003 году было выпущено 275 тыс. штук телевизоров.

ОВпл. = 260/200=1,3 (130%)

ОВвпл. = 275/260=1,06 (106%)

ОВд. = 275/200=1,375 (137,5%)

4. Относительная величина структуры. Определяется, как отношение части совокупности ко всей совокупности в целом и, выраженная в процентах, называется удельным весом.

5. Относительная величина координации. Определяется, как отношение двух частей одной и той же совокупности. Как правило, самая маленькая по количественному значению часть выбирается в качестве базы сравнения, и все остальные части исходной совокупности сравнивают с этой выбранной частью. Пример: из общей численности населения РФ на начало 2003 года (145,2 млн. человек): городское население составляет 106,4 млн. чел., сельское – 38,8 млн. чел..

 

ОВстр. = 106,4/145,2=0,73 (73%)

ОВстр. = 38,8/145,2=0,27 (27%)

ОВк = 106,4/38,8 = 2,7

6. Относительная величина сравнения. Определяется, как отношение между двумя одноименными величинами, взятыми за один и тот же период времени, но относящимися к различным совокупностям. Пример: численность российских граждан. Выехавших в 2002 году на постоянное жительство в другие страны характеризуется данными (человек): в Германию – 42231, в Израиль – 2764, в США -3134.

ОВср. = 42231/2764=15,3

ОВср. = 3134/2764=1,1

7. Относительная величина интенсивности. Это единственная из относительных величин, имеющая единицы измерения, причем, они различны в числителе и знаменателе. Относительную величину интенсивности характеризует степень распространения изучаемого явления в определенной среде. Пример: на начало 2003 года численность населения нашей страны составила 145.2 млн. чел.. Территория страны 17,075 млн. км².

ОВинт. = 145,2 млн. чел./ 17,075 млн. км² =8,5 чел/км²

Относительные величины интенсивности часто называют показателями уровня экономического и социального развития, т. к. в их число входят: объем ВВП на душу населения в год (руб./чел.), потребление основных продуктов питания на человека в год (кг/чел.), обеспеченность населения жильем (м²/чел.) и т. д.

Средние величины.

Средняя величина является одной из важнейших обобщающих характеристик статистики. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами, и находят выражение общие и закономерные черты, свойственные всей совокупности в целом. Индивидуальные значения признака (варианты), из которых вычисляется средняя величина, должны быть одного и того же вида, т. е. должны характеризовать однородные явления и иметь одинаковые единицы измерения.

В каждом конкретном случае средняя величина имеет определенное, социально-экономическое содержание, обусловленное природой изучаемого объекта. Например: Средняя зарплата первого сотрудника определяется путем деления фонда оплаты труда на численность сотрудников. Средний размер вклада в банке определяется путем деления суммы все вкладов.

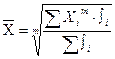В статистике вычисляют степенные и структурные средние величины. Общая формула степенных средних величин имеет следующий вид: . В этой формуле X_i – индивидуальное значение признаков (варианты); ƒ_i – соответствующие частоты (частости); m – показатель степени. Различают следующие виды степенных средних величин: 1) При m = 1 → средняя арифметическая величина. 2) При m = -1 → средняя гармоническая величина. 3) При m = 0 → средняя геометрическая величина. 4) При m = 2 → средняя квадратичная величина. 5) При m = 3 → средняя кубическая величина.

Выбор формулы для расчета средней величины зависит от имеющейся исходной информации.