
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет среднего уровня в рядах динамики.Содержание книги Поиск на нашем сайте
Различают: y1 - начальный уровень ряда, yn – конечный уровень ряда, 1) Если приводятся данные только на начало и на конец изучаемого периода, то средний уровень рассчитывается, как средняя арифметическая величина из этих двух значений. 2) Если моменты времени, к которым относятся уровни ряда расположены через равные промежутки, то средний уровень определяется по формуле простой хронологической средней: 3) Если моменты времени, к которым относятся уровни ряда расположены через не равные промежутки, то средний уровень рассчитывается по формуле хронологической взвешенной: В интервальном ряду динамики средний уровень рассчитывается следующим образом: 1. В ряду с равноотстоящими интервалами по формуле простой арифметической средней: 2. В ряду с не равноотстоящими интервалами по формуле средней арифметической взвешенной: Основные аналитические и средние показатели рядов динамики. Кроме среднего уровня для анализа рядов динамики вычисляют следующие аналитические показатели: 1) Абсолютный прирост ( 2) Коэффициент роста (Кр) 3) Темп роста (Тр) 4) Темп прироста (Тпр) 5) Абсолютное значение 1% прироста (Аi) Возможны 2 варианта сравнения уровней рядов динамики. При 1-ом варианте сравнения каждый i-ый уровень ряда сравнивают с каким-то первым уровнем, выбранным в качестве базы сравнения. Как правило, в качестве базы сравнения выбирают уровень начального периода. Полученные в результате сравнения показатели называются базисными и характеризуют изменение изучаемого показателя в данном периоде, по сравнению с начальным периодом. При втором варианте сравнения каждый i-ый уровень ряда сравнивают с предшествующим уровнем, т. е. база сравнения все время меняется. Рассчитанные при этом варианте показатели называются цепными и характеризуют изменение изучаемого показателя в данном периоде по сравнению с предшествующим. 1) Абсолютный прирост показывает на сколько единиц изменится уровень данного периода, по сравнению с уровнем, выбранным в качестве базы сравнения. Базисные показатели: 2) Коэффициент роста показывает, во сколько раз изменился уровень данного периода по сравнению с уровнем, выбранным в качестве базы сравнения.
3) Темп роста представляет собой коэффициент роста, выраженный в процентах (%):
4) Темп прироста характеризует относительное изменение уровней ряда, выраженное в %:
5) Абсолютное значение 1% прироста показывает на сколько единиц изменился уровень ряда динамики при его изменении на 1%: Кроме перечисленных аналитических показателей вычисляют средние показатели динамики за определенный период времени. Вычисляют: 1) среднегодовой абсолютный прирост, который показывает на сколько единиц изменялись уровни ряда динамики ежегодно, в течение определенного периода времени: 2) среднегодовой коэффициент роста, который показывает, во сколько раз ежегодно изменялись уровни ряда динамики в течение определенного периода времени:
3) среднегодовой темп роста представляет собой среднегодовой коэффициент роста, выраженный в процентах (%):
4) среднегодовой темп прироста показывает на сколько процентов ежегодно изменялись уровни ряда динамики в течение определенного периода времени:
Лекция №9. При сравнении двух и более рядов динамики возникает проблема несопоставимости уровней ряда по следующим причинам: 1) изменение территориальных границ, в пределах которых рассчитываются показатели; 2) изменение уровня цен при расчете показателей; 3) изменение методологии расчета покупателей. Для привидения таких рядов динамики к сопоставимому виду применяют метод смыкания рядов динамики. Он заключается в том, что для периода, в котором произошли определенные изменения, в расчете показателей рассчитывают коэффициент соотношения уровней и затем все последующие (предшествующие), уровни рядов динамики корректируют с учетом этого коэффициента. При изучении рядов динамики важной задачей является выявление основной тенденции изменения уровней рядов динамики. Для этого используют следующие методы: 1) Метод скользящей средней, который заключается в том, что по исходным данным для каждого звена по формуле простой арифметической средней рассчитываются теоретические уровни, в которых исключены случайные колебания уровней рядов динамики. Полученные теоретические уровни присваивают периоду, который находится в середине каждого звена. Например, трехзвенную скользящую среднюю рассчитывают следующим образом: 2) Метод укрупнения интервалов состоит в том, что первоначальный ряд динамики преобразуется в ряд с более продолжительными периодами времени. Например: месячные уровни товарооборота преобразуют в квартальные уровни. 3) Метод механического выравнивания заключается в том, что на основе рассчитанного среднегодового абсолютного прироста вычисляются теоретические уровни ряда динамики. 4) Метод аналитического выравнивания состоит в том, что на основе математической функции, которая наиболее точно отражает основную тенденцию изменения уровней ряда динамики, строится теоретическая функция: y(t)=f(t), где t – параметр времени. При подборе математической функции необходимо свести к минимуму сумму квадратов отклонений фактических уровней ряда от теоретических: Пример:
5) Метод интерполяции заключается в том, что на основе выявленных закономерностей изменения уровней ряда динамики рассчитываются неизвестные уровни внутри этого ряда динамики. 6) Метод экстраполяции состоит в том, что на основе выявленной закономерности в изменении уровней ряда строится прогноз на перспективный период времени. Для этого используются следующие формулы:
Где
Лекция №10 Экономические индексы. Экономический индекс – это относительный показатель, получаемый в результате сопоставления уровней социально экономического явления во времени, в пространстве и по сравнению с планом. С помощью экономических индексов решаются 2 основные задачи: 1) дается характеристика общего изменения сложного экономического явления; 2) в общем изменении сложного экономического явления выделяют влияние основных факторов, абстрагируясь от второстепенных. Для удобства, в теории экономических индексов принята следующая система обозначений: p – цена единицы продукции данного вида q – количество продукции данного вида в натуральном выражении (физический объем продукции) p*q – стоимость продукции данного вида (товарооборот продукции) z – затраты на производство единицы продукции данного вида (себестоимость продукции) z*q – затраты на производство всей продукции данного вида (издержки производства) w – производительность труда N – численность работников T – количество отработанного времени. По обхвату элементов исходной совокупности экономические индексы делятся на индивидуальные и общие (сводные). В свою очередь общие экономические индексы в зависимости от способа расчета подразделяются на агрегатные и средние. Индивидуальный экономический индекс рассчитывается только по одному элементу исходной совокупности и обозначается через i. Статистический показатель, изменение которого мы определяем, называется индексируемым и сносится справа внизу от обозначения экономического индекса. Например: ip – индивидуальный индекс цены; iq – индивидуальный индекс физического объема продукции; ipq – индивидуальный индекс стоимости продукции (товарооборот). По определению, индивидуальный индекс любого показателя определяется, как отношение величины данного показателя в отчетном периоде к величине этого же показателя в базисном периоде. Например: Между экономическими индексами определенных показателей, существует такая же взаимосвязь, какая существует между самими этими показателями. Эта взаимосвязь сохраняется и для индивидуальных и для общих экономических индексов. Например, стоимость продукции определяется, как произведение цены единичной продукции на количество изделий, значит, индивидуальный индекс стоимости продукции должен быть равен произведению индексов цены и физического объема продукции.(ipq=ip*iq) Разность числителя и знаменателя соответствующего экономического индекса показывает абсолютное изменение изучаемого показателя в отчетном периоде, по сравнению с базисным периодом. Например: Общие экономические индексы рассчитываются по всем элементам исходной совокупности в целом и обозначаются Y. Агрегатный индекс цены вычисляют по формуле:
Правило 1. Если индексируется (изменяется) качественный показатель (цена, себестоимость, производительность и т. д.), то количественный показатель (физический объем продукции, численность работников и т. д.) фиксируется на уровне отчетного периода.
Величина данного индекса характеризует относительное изменение стоимости всей произведенной (проданной) продукции в отчетном периоде по сравнению с базисным только за счет изменения уровня цен по каждому виду продукции. Разность числителя и знаменателя индекса ( В нашей стране вычисляют агрегатный индекс цены Ласпейраса. Он рассчитывается по формуле: Правило 2. Если индексируется (изменяется) коллективный показатель, то качественный фиксируют на уровне базисного периода. Общий индекс стоимости продукции (товарооборота) вычисляется по формуле:
Величина данного индекса характеризует относительное изменение стоимости всей продукции в отчетном периоде по сравнению с базисным за счет двух факторов: 1) изменение уровня цен каждого вида продукции; 2) изменение количества продукции каждого вида. Разность числителя и знаменателя ( Пример вычисления экономических индексов: по одному из магазинов имеются следующие данные (цифры условные):
Лекция №11
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 999; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.235.66 (0.007 с.) |

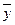 - средний уровень ряда. В моментном ряду динамики возможны следующие варианты расчета среднего уровня:
- средний уровень ряда. В моментном ряду динамики возможны следующие варианты расчета среднего уровня: , где n – число уровней ряда.
, где n – число уровней ряда.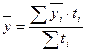 , где
, где  - полусумма двух соседних уровней ряда;
- полусумма двух соседних уровней ряда;  - промежуток между двумя соседними уровнями ряда, выраженный в днях, месяцах и т. д. в зависимости от исходных данных.
- промежуток между двумя соседними уровнями ряда, выраженный в днях, месяцах и т. д. в зависимости от исходных данных. .
. .
. )
) ; цепные показатели:
; цепные показатели: 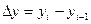 .
. (б.)
(б.)  (ц.)
(ц.) (б.)
(б.)  (ц.)
(ц.) (б.)
(б.) 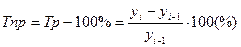 (ц.)
(ц.) .
. , где m – число цепных абсолютных приростов.
, где m – число цепных абсолютных приростов.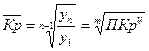
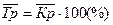 .
. .
. ;
;  ;
;  , и т. д.
, и т. д. . Рассмотрим аналитическое выравнивание ряда динамики по линейной функции
. Рассмотрим аналитическое выравнивание ряда динамики по линейной функции  , где t – параметр времени; a и b – параметры линейной функции. Для определения параметров линейной функции a и b составляют систему уравнений:
, где t – параметр времени; a и b – параметры линейной функции. Для определения параметров линейной функции a и b составляют систему уравнений: 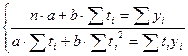 .
.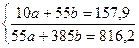 ; b = -0,63; a =19,3;
; b = -0,63; a =19,3;  .
.

 - конечный уровень ряда; t – срок прогноза;
- конечный уровень ряда; t – срок прогноза;  - среднегодовой абсолютный прирост за изучаемый период времени;
- среднегодовой абсолютный прирост за изучаемый период времени;  - среднегодовой коэффициент роста за изучаемый период времени;
- среднегодовой коэффициент роста за изучаемый период времени;  - перспективное значение уровня цен ряда динамики.
- перспективное значение уровня цен ряда динамики. , где p1 и p0, соответственно, цена единицы продукции данного вида в отчетном и базисного периодах.
, где p1 и p0, соответственно, цена единицы продукции данного вида в отчетном и базисного периодах. - показывает на сколько рублей изменилась цена единичной продукции данного вида в отчетном периоде по сравнению с базисным.
- показывает на сколько рублей изменилась цена единичной продукции данного вида в отчетном периоде по сравнению с базисным. - этот индекс называют индексом Пааше.
- этот индекс называют индексом Пааше.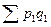 - это стоимость всей произведенной (проданной) продукции отчетного периода;
- это стоимость всей произведенной (проданной) продукции отчетного периода;  - это стоимость всей произведенной (проданной) продукции отчетного периода в базисных ценах.
- это стоимость всей произведенной (проданной) продукции отчетного периода в базисных ценах.
 -
-  . Агрегатный индекс физического объема продукции вычисляют по формуле:
. Агрегатный индекс физического объема продукции вычисляют по формуле: 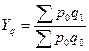 .
. - Это стоимость всей произведенной (проданной) продукции в базисном периоде. Величина данного индекса характеризует относительное изменение стоимости всей произведенной (проданной) продукции в отчетном периоде по сравнению с базисным только за счет изменения количества продукции каждого вида. Разность числителя и знаменателя (
- Это стоимость всей произведенной (проданной) продукции в базисном периоде. Величина данного индекса характеризует относительное изменение стоимости всей произведенной (проданной) продукции в отчетном периоде по сравнению с базисным только за счет изменения количества продукции каждого вида. Разность числителя и знаменателя (
 -
- 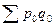 ) характеризует абсолютное изменение стоимости всей продукции в отчетном периоде по сравнению с базисным только за счет изменения количества продукции каждого вида.
) характеризует абсолютное изменение стоимости всей продукции в отчетном периоде по сравнению с базисным только за счет изменения количества продукции каждого вида. .
.
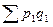 -
- 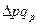 +
+  ;
; 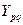 =
=  *
*  .
.
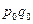


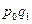
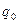


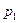
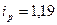 (119%) – означает, что цена 1 кг проданных помидоров увеличилась в отчетном периоде по сравнению с базисным в 1,19 раза или на 19%.
(119%) – означает, что цена 1 кг проданных помидоров увеличилась в отчетном периоде по сравнению с базисным в 1,19 раза или на 19%.


