
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема №3. «Абсолютные, относительные и средние величины»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Практическое занятие №1. Контрольные вопросы 1. Дайте понятие абсолютной величины и назовите особенности абсолютных величин как статистических показателей. 2. Назовите единицы измерения абсолютных статистических показателей. 3. Почему абсолютные статистические показатели не могут всесторонне характеризовать социально - экономические процессы и явления? 4. Дайте понятие относительного статистического показателя и сформулируйте основное условие правильного расчета относительной величины. 5. Назовите основные виды относительных величин. Решение типовых задач Пример 2.1. В базисном периоде фирма продала 200 автомобилей. По плану на текущий период намечалось продать 210 автомобилей. Фактически в текущем периоде было продано 215 автомобилей. Определите относительные показатели плана, выполнения плана и динамики. Покажите связь между найденными показателями. Решение: Согласно условию имеем: базисное значение показателя – 200 автомобилей; планируемое значение показателя – 210 автомобилей; текущее значение показателя – 215 автомобилей; Вычисляем: Относительный показатель плана, используя формулу:
Относительный показатель выполнения (реализации) плана вычисляем по формуле:
Для вычисления относительного показателя динамики используем формулу:
Для проверки решения задачи используем формулу связи между относительными показателями плана, реализации плана и динамики:
Проверка: Ответ: 1) 2) 3) Пример 2.2. Планировалось повысить успеваемость по статистике на 20%. План был перевыполнен на 4%. Определите относительный показатель динамики. Решение: Согласно условию задачи имеем: Относительный показатель плана равен Относительный показатель реализации плана составил Между относительными показателями плана, реализации плана и динамики существует следующая взаимосвязь:
Поэтому относительный показатель динамики равен: Ответ: успеваемость по статистике повысилась на 24,8% в текущем периоде по сравнению с базисным. Пример 2.3. Имеются следующие данные о составе работающей молодежи по полу, возрасту и месту проживания:
Определите: 1) структуру работающей молодежи по полу 2) относительные показатели координации по полу. Сделайте анализ полученных результатов. Решение Для ответа на вопросы задачи оставим в таблице данных только первую и две последние строки:
1) Относительный показатель структуры (ОПС) характеризует состав изучаемых совокупностей, т.е. показывает долю отдельных частей в общем объеме совокупности и вычисляется по формуле:
Решение задачи оформим в таблице:
ОПС в данном случае выразили в процентах. Полученные результаты представляют собой удельные веса. 2) Относительные показатели координации (ОПК) характеризуют соотношение отдельных частей целого между собой (и применяются для сравнения различных частей совокупности между собой):
Ответ: 1) удельный вес мужчин, занятых в экономике, выше удельного веса женщин, занятых в экономике. Наибольший удельный вес мужчин, занятых в экономике, имеет категория мужчин в возрасте 16-19 лет и составляет 61,24%. 2) ОПК показывает, что на 1 женщину, занятую в экономике приходится 1,58 мужчин в возрасте 16-19 лет (или на 100 женщин приходится 158 мужчин) и т.д.
Задачи для самостоятельного решения 2.1. На основе приведенных ниже данных о составе экономически активного населения Российской Федерации рассчитайте все возможные относительные показатели динамики. Численность экономически активного населения, тыс. чел.
2.2. В базисном периоде затраты на производство продукции составляли 1200 тыс. руб. В текущем периоде они достигли 1050 тыс. руб. при плане 1110 тыс. руб. Определите относительные показатели плана, выполнения плана и динамики. Проверьте правильность решения, используя связь между показателями.
2.3. Объем производства конфет «Наташа» планировалось увеличить в 1,15 раза. Фактически объем производства этих конфет увеличился по сравнению с базисным периодом на 17,5%. Определите относительный показатель выполнения плана.
2.4. Производительность труда в цехе по сравнению с базисным периодом увеличилась на 5%, а по сравнению с планом на 3,5%. Определите относительный показатель плана.
2.5. Планировалось повысить успеваемость по статистике на 20%. План был перевыполнен на 4%. Определите относительный показатель динамики.
2.6. Имеются следующие данные о составе работающей молодежи по полу, возрасту и месту проживания:
Определите: 1) структуру работающей молодежи по возрасту и месту проживания; 2) структуру работающей молодежи в городах по возрасту; 3) структуру занятых мужчин и женщин по возрасту; 4) относительные показатели координации по возрасту и месту проживания работающей молодежи; 5) относительные показатели координации по месту проживания лиц в возрасте 20–24 года. Сделайте анализ полученных результатов.
2.7. По имеющимся данным проведите анализ изменения обеспеченности населения РФ врачами. Как называются относительные величины, характеризующие эту обеспеченность?
2.8. Имеются следующие данные о составе работающей молодежи по полу, возрасту и месту проживания:
Рассчитайте все возможные относительные показатели сравнения. Практическое занятие № 2. Контрольные вопросы 1. Назовите основные требования к расчету средних величин. 2. Какие виды средних вы знаете? В каких случаях они используются? 3. Приведите формулы расчета средних различных видов сложных величин. 4. Какие виды структурных средних вы знаете? В каких случаях они используются? 5. Приведите формулы расчета структурных средних для интервального ряда. 6. Сформулируйте свойство мажорантности средних.
Решение типовых задач Пример 3.1. Имеются следующие данные о деятельности группы предприятий некоторой отрасли:
Определите в целом по всей совокупности предприятий отрасли: 1) средний объем продукции в расчете на одного работника, 2) средний размер произведенной продукции в расчете на одно предприятие, 3) средний уровень затрат в расчете на один рубль произведенной продукции. Постройте гистограмму распределения затрат на 1 руб. произведённой продукции по данной группе предприятий. Решение: 1) Для ответа на 1-й вопрос задачи воспользуемся информацией, представленной в 4-ом столбце таблицы. Для определения среднего объема продукции в расчете на одного работника по данной совокупности (обозначим этот показатель как
Итак, получаем: 2) Для ответа на 2-й вопрос задачи воспользуемся информацией, представленной в 3-ем столбце таблицы. Для определения среднего размера произведенной продукции в расчете на одно предприятие по данной совокупности (обозначим этот показатель как
3) Для ответа на 3-й вопрос задачи воспользуемся информацией, представленной в 1-ом и 2-ом столбцах таблицы. Средняя арифметическая может рассчитываться как по данным дискретных (первый и второй случай данной задачи), так и интервальных вариационных рядов, когда значение варьирующего признака представлены в виде интервалов (от и до) как в данном случае. Для вычисления средней величины в данном случае надо для каждого интервала найти серединное значение После того, как определено серединное значение интервала, производится расчет средней арифметической взвешенной по формуле:
Получаем, что средний уровень затрат в расчете на один рубль произведенной продукции равен:
4) Построим гистограмму распределения затрат на 1 руб. произведённой продукции по данной группе предприятий.
Пример 3.1. Имеются следующие данные о распределении вкладов по их размеру:
Определите: 1) модальный размер вклада; 2) медианный размер вклада. Решение: 1) Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
где Модальным интервалом называется интервал с наибольшей частотой. Анализ условия показывает, что модальным является 6-й интервал, для которого Итак, имеем:
Далее вычисляем:
2) Медиана - это варианта, расположенная в середине упорядоченного вариационного ряда. Медиана интервального вариационного ряда распределения определяется по формуле
где
Медианным интервалом будет являться интервал, кумулята частот которого будет равна или превышать половину суммы частот. Для данной задачи формула будет иметь вид:
Для нахождения медианного интервала в таблице-условии добавим столбец «Кумулята удельных весов» и заполним его. Таблица примет вид:
Далее находим:
Вычисляем:
Задачи для самостоятельного решения 3.1. Имеется ряд распределения:
1) Рассчитайте средний тарифный разряд рабочих с точностью целых. 2) Определите моду и медиану распределения 3) Постройте кумуляту распределения.
3.2. Имеются следующие данные о числе договоров страхования, заключенных агентами фирмы за отчетный период:
Постройте дискретный вариационный ряд распределения и определите среднее число заключенных договоров страхования одним страховым агентом, моду и медиану.
3.3. Имеются следующие данные за смену о затратах времени на обработку деталей рабочими цеха:
Определите среднее количество времени, затрачиваемое одним рабочим на обработку детали. 3.4. Производство электроэнергии характеризуется следующими данными, млрд. кВт:
Определите средний уровень производства электроэнергии за 1998–2005 гг. 3.5. Имеются следующие данные по региону:
Определите по региону в целом: 1) среднедушевой доход; 2) среднее потребление мяса на душу населения; 3) средний размер семьи; 4) среднее число семей в городе; 5) медианное значение среднедушевого дохода; 6) модальное значение среднедушевого дохода.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 5509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.19.251 (0.013 с.) |

 или
или 
 или
или 
 или
или 

 , т.е. получили численное значение относительного показателя динамики.
, т.е. получили численное значение относительного показателя динамики. , т.е. фирма планировала увеличить объем продаж автомобилей на 5% (105%-100%)
, т.е. фирма планировала увеличить объем продаж автомобилей на 5% (105%-100%) , т.е. фирма продала автомобилей на 2,4% больше планируемого
, т.е. фирма продала автомобилей на 2,4% больше планируемого , т.е. объем продаж автомобилей увеличился в текущем периоде на 7,5% по сравнению с базисным периодом.
, т.е. объем продаж автомобилей увеличился в текущем периоде на 7,5% по сравнению с базисным периодом. или 1,2
или 1,2 или 1,04
или 1,04 или 124,8%
или 124,8% В данном случае показателем по всей совокупности в целом является показатель «всего занято в экономике».
В данном случае показателем по всей совокупности в целом является показатель «всего занято в экономике». . В качестве базы сравнения выберем число женщин, занятых в экономике, или удельный вес женщин, занятых в экономике. Результаты вычислений оформим в таблице:
. В качестве базы сравнения выберем число женщин, занятых в экономике, или удельный вес женщин, занятых в экономике. Результаты вычислений оформим в таблице: ) воспользуемся формулой средней арифметической простой:
) воспользуемся формулой средней арифметической простой: , где
, где  – число групп предприятий в данной совокупности.
– число групп предприятий в данной совокупности.
 ) воспользуемся формулой средней арифметической простой:
) воспользуемся формулой средней арифметической простой: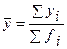 , здесь
, здесь  – число предприятий в группе. Итак, получаем:
– число предприятий в группе. Итак, получаем: 
 , которое определяется как полусумма значений нижней и верхней границ. В открытых интервалах предполагается, что величина открытого интервала равна величине соседнего интервала.
, которое определяется как полусумма значений нижней и верхней границ. В открытых интервалах предполагается, что величина открытого интервала равна величине соседнего интервала. Все вычисления выполним в таблице:
Все вычисления выполним в таблице:



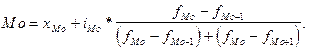
 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;  - величина модального интервала;
- величина модального интервала;  - частота модального интервала;
- частота модального интервала;  – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; 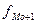 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным. , здесь
, здесь  – число всех вкладов,
– число всех вкладов,  – число вкладов в данной группе. Заметим, что в формуле для вычисления моды можно заменить веса
– число вкладов в данной группе. Заметим, что в формуле для вычисления моды можно заменить веса  , т.е. формула будет иметь вид:
, т.е. формула будет иметь вид: 
 - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду; - ширина модального интервала;
- ширина модального интервала; - удельный вес модального интервала;
- удельный вес модального интервала; - удельный вес интервала, предшествующего модальному;
- удельный вес интервала, предшествующего модальному; - удельный вес интервала, следующего за модальным..
- удельный вес интервала, следующего за модальным.. , т.е. большая часть вкладов имеет размер порядка 11790 руб.
, т.е. большая часть вкладов имеет размер порядка 11790 руб.
 — начальное значение интервала, содержащего медиану;
— начальное значение интервала, содержащего медиану; 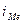 — величина медианного интервала;
— величина медианного интервала;  — сумма частот ряда;
— сумма частот ряда;  — сумма (кумулята) накопленных частот, предшествующих медианному интервалу;
— сумма (кумулята) накопленных частот, предшествующих медианному интервалу; — частота медианного интервала.
— частота медианного интервала.


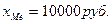 – начальное значение интервала, содержащего медиану;
– начальное значение интервала, содержащего медиану;  – величина медианного интервала;
– величина медианного интервала;  – сумма удельных весов ряда;
– сумма удельных весов ряда;  — сумма (кумулята) накопленных удельных весов, предшествующих медианному интервалу;
— сумма (кумулята) накопленных удельных весов, предшествующих медианному интервалу;  — удельный вес медианного интервала.
— удельный вес медианного интервала. , т.е. 50% вкладов имеет размер менее 10750руб., а 50% вкладов – более 10750 руб.
, т.е. 50% вкладов имеет размер менее 10750руб., а 50% вкладов – более 10750 руб.


