
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительная величина сравненияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Относительная величина сравнения (показатель сравнения) — характеризует соотношение между разными совокупностями по одноименным показателям. Пример 8: Объем выданных кредитов частным лицам на 1 февраля 2008 г. Сбербанком России составил 520189 млн.руб, по Внешторгбанку — 10915 млн.руб.
13.Определение относительных показателей динамики: темпов роста, плана, реализации плана, структуры, координации, интенсивности, сравнения. Относительные величины, используемые в статистической практике:
Относительная величина структуры (ОВС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объеме совокупности. ОВС рассчитывают как отношение объема части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объеме совокупности (%):
где mi - объем исследуемой части совокупности; M - общий объем исследуемой совокупности.
где mi - одна из частей исследуемой совокупности; mб - часть совокупности, которая является базой сравнения.
где Рпл - плановый показатель; Р0 - фактический (базовый) показатель в предшествующем периоде.
где Рф - величина выполнения плана за отчетный период; Рпл - величина плана за отчетный период.
Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста - ОВДб), так и с переменным базовым уровнем (цепные темпы роста - ОВДц):
где Рт - уровень текущий; Рб - уровень базисный;
где Рт - уровень текущий; Рт-1 - уровень, предшествующий текущему.
где МА - показатель первого одноименного исследуемого объекта; МБ - показатель второго одноименного исследуемого объекта (база сравнения). Все предыдущие показатели относительных величин характеризовали соотношения одноименных статистических объектов. Однако есть группа относительных величин, которые характеризуют соотношение разноименных, но связанных между собой статистических показателей. Эту группу называют группой Примерами относительных величин интенсивности могут служить, скажем, показатели уровня технического развития производства, уровня благосостояния граждан, показатели обеспеченности населения средствами массовой информации, предметами культурно-бытового назначения и т.д. ОВИ рассчитывается по формуле
где А - распространение явления; ВА - среда распространения явления А. При расчете относительных величин интенсивности может возникнуть проблема выбора адекватной явлению базы сравнения (среды распространения явления). Например, при определении показателя плотности населения нельзя брать в качестве базы сравнения общий размер территории того или иного государства, в этом случае базой сравнения может быть лишь территория в 1 км2. Критерием правильности расчета является сопоставимость по разработанной методологии расчета сравниваемых показателей, применяющихся в статистической практике.
14.Сущность и виды средних. Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности. Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака. Так, например, средняя заработная плата дает обобщающую количественную характеристику состояния оплаты труда рассматриваемой совокупности работников. Кроме того, используя средние величины, имеется возможность сопоставлять различные информационные совокупности. Так, например, можно сравнивать различные организации по уровню производительности труда, а также по уровню фондоотдачи, материалоотдачи и по другим показателям. Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором. Статистическая обработка методом средних величин заключается в замене индивидуальных значений варьирующего признака Виды средних величин Средние величины делятся на два больших класса: степенные средние и структурные средние Степенные средние:
Гармоническая — используется в тех случаях когда известны индивидуальные значения признака В примере ниже Среднегармоническую величину можно определить по следующей формуле:
Геометрическая Среднегеометрическая величина дает возможность сохранять в неизменном виде не сумму, а произведение индивидуальных значений данной величины. Ее можно определить по следующей формуле:
Среднегеометрические величины наиболее часто используются при анализе темпов роста экономических показателей Квадратическая Средние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической. Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:
Структурные средние:
Выбор формы средней величины зависит от исходной базы расчета средней и от имеющейся экономической информации для ее расчета. Исходной базой расчета и ориентиром правильности выбора формы средней величины являются экономические соотношения, выражающие смысл средних величин и взаимосвязь между показателями.
15.Область применения и расчет средней арифметической простой и взвешенной. Основные свойства средней арифметической и их применения. Самым распространенным видом средней является средняя арифметическая.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 2284; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.224 (0.007 с.) |

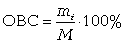 (4.1)
(4.1) Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%):
Относительная величина координации (ОВК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%):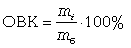 (4.2)
(4.2)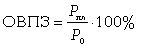 (4.3)
(4.3)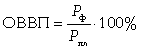 (4.4)
(4.4) (4.5)
(4.5)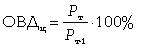 (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8)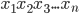 некоторой уравновешенной средней величиной
некоторой уравновешенной средней величиной 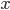 .
.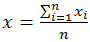
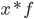 , а частоты
, а частоты 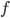 неизвестны.
неизвестны.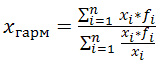
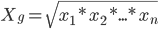
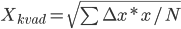
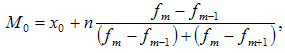
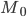 — значение моды
— значение моды — нижняя граница модального интервала
— нижняя граница модального интервала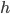 — величина интервала
— величина интервала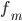 — частота модального интервала
— частота модального интервала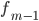 — частота интервала, предшествующего модальному
— частота интервала, предшествующего модальному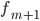 — частота интервала, следующего за модальным
— частота интервала, следующего за модальным


