Графическое изображение рядов распределения

Наглядно ряды распределения представляются при помощи графических изображений.

Ряды распределения изображаются в виде:

• Полигона
• Гистограммы
• Кумуляты
• Огивы

Полигон

При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.

Полигон на рис. 6.1 построен по данным микропереписи населения России в 1994 г.

Домохозяйства, состоящие из:	одного человека	двух человек	трех человек	5 или более	всего
Число домохозяйств в %	19,2	26,2	22,6	20,5	100,0

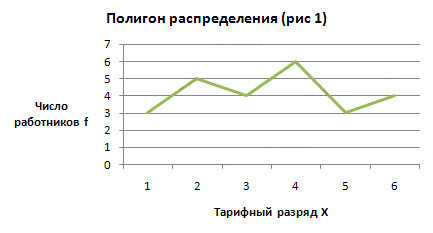
Распределение домохозяйств по размеру

Условие: Приводятся данные о распределении 25 работников одного из предприятий по тарифным разрядам:
4; 2; 4; 6; 5; 6; 4; 1; 3; 1; 2; 5; 2; 6; 3; 1; 2; 3; 4; 5; 4; 6; 2; 3; 4
Задача: Построить дискретный вариационный ряд и изобразить его графически в виде полигона распределения.
Решение:
В данном примере вариантами является тарифный разряд работника. Для определения частот необходимо рассчитать число работников, имеющих соответствующий тарифный разряд.

Тарифный разряд Xi	Число работников fi
Итого:

Полигон используется для дискретных вариационных рядов.

Для построения полигона распределения (рис 1) по оси абсцисс (X) откладываем количественные значения варьирующего признака — варианты, а по оси ординат — частоты или частости.

Если значения признака выражены в виде интервалов, то такой ряд называется интервальным.
Интервальные ряды распределения изображают графически в виде гистограммы, кумуляты или огивы.

Статистическая таблица

Условие: Приведены данные о размерах вкладов 20 физических лиц в одном банке (тыс.руб) 60; 25; 12; 10; 68; 35; 2; 17; 51; 9; 3; 130; 24; 85; 100; 152; 6; 18; 7; 42.
Задача: Построить интервальный вариационный ряд с равными интервалами.
Решение:

1. Исходная совокупность состоит из 20 единиц (N = 20).
2. По формуле Стерджесса определим необходимое количество используемых групп: n=1+3,322*lg20=5
3. Вычислим величину равного интервала: i=(152 — 2) /5 = 30 тыс.руб
4. Расчленим исходную совокупность на 5 групп с величиной интервала в 30 тыс.руб.
5. Результаты группировки представим в таблице:

Размер вкладов тыс.руб Xi	Число вкладов fi	Число вкладов в % к итогу Wi
2 — 32
32 — 62
62 — 92
92 — 122
122 — 152
Итого:

При такой записи непрерывного признака, когда одна и та же величина встречается дважды (как верхняя граница одного интервала и нижняя граница другого интервала), то эта величина относится к той группе, где эта величина выступает в роли верхней границы.

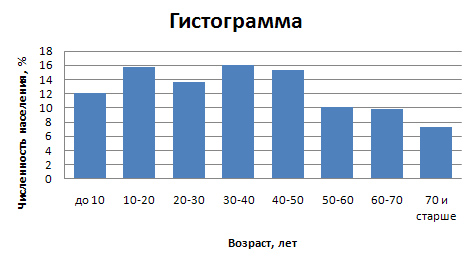
Гистограмма

Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).

На рис. 6.2. изображена гистограмма распределения населения России в 1997 г. по возрастным группам.

Все население	В том числе в возрасте
	до 10	10-20	20-30	30-40	40-50	50-60	60-70	70 и старше	Всего
Численность населения	12,1	15,7	13,6	16,1	15,3	10,1	9,8	7,3	100,0

Рис. 6.2. Распределение населения России по возрастным группам

Условие: Приводится распределение 30 работников фирмы по размеру месячной заработной платы

Размер заработной платы руб. в месяц	Численность работников чел.
до 5000
5000 — 7000
7000 — 10000
10000 — 15000
Итого:

Задача: Изобразить интервальный вариационный ряд графически в виде гистограммы и кумуляты.
Решение:

1. Неизвестная граница открытого (первого) интервала определяется по величине второго интервала: 7000 — 5000 = 2000 руб. С той же величиной находим нижнюю границу первого интервала: 5000 — 2000 = 3000 руб.
2. Для построения гистограммы в прямоугольной системе координат по оси абсцисс откладываем отрезки, величины которых соответствуют интервалам варицонного ряда.
   Эти отрезки служат нижним основанием, а соответствующая частота (частость) — высотой образуемых прямоугольников.
3. Построим гистограмму:

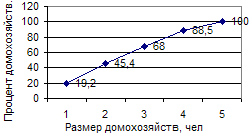
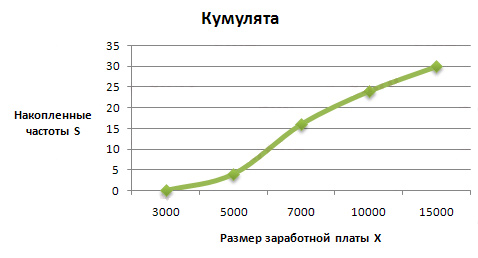
Для построения кумуляты необходимо рассчитать накопленные частоты (частости). Они определяются путем последовательного суммирования частот (частостей) предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое.

Кумулята

Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты.

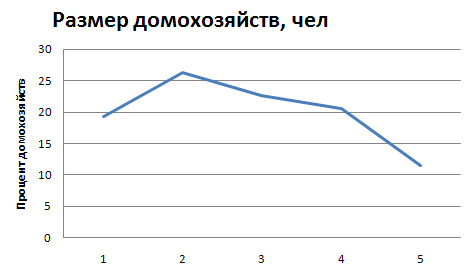
Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости (рис. 6.3).

Рис. 6.3. Кумулята распределения домохозяйств по размеру

4. Рассчитаем накопленные частоты:
Наколенная частота первого интервала рассчитывается следующим образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.

Размер заработной платы руб в месяц Xi	Численность работников чел. fi	Накопленные частоты S
до 5000
5000 — 7000
7000 — 10000
10000 — 15000
Итого:		-

При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:

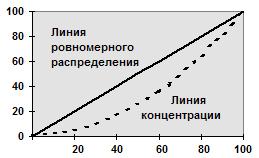
Огива

Огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.

Разновидностью кумуляты является кривая концентрации или график Лоренца. Для построения кривой концентрации на обе оси прямоугольной системы координат наносится масштабная шкала в процентах от 0 до 100. При этом на оси абсцисс указывают накопленные частости, а на оси ординат — накопленные значения доли (в процентах) по объему признака.

Равномерному распределению признака соответствует на графике диагональ квадрата (рис. 6.4). При неравномерном распределении график представляет собой вогнутую кривую в зависимости от уровня концентрации признака.

 

12.Виды абсолютных и относительных показателей.

Статистический показатель — количественная характеристика социально-экономических явлений и процессов в условиях качественной определенности.

Различают показатель-категорию и конкретный статистический показатель:

Показатель категория определяет содержание статистического показателя, то есть не численное значение определенного показателя, а его элементы: например коэффициент рождаемости, смертности, национального богатства.

Конкретный статистический показатель — это цифровая характеристика изучаемого явления или процесса. Например: численность населения России на данный момент составляет 145 млн.человек.

По форме различают статистические показатели:

• Абсолютные
• Относительные
• Средние

По охвату единиц различают индивидуальные и сводные показатели.

Индивидуальные показатели — характеризуют отдельный объект или отдельную единицу совокупности (прибыль фирмы, размер вклада отдельного человека).

Сводные показатели — характеризуют часть совокупности или в всю статистическую совокупность в целом. Их можно получить как объемные и расчетные. Объемные показатели получают путем сложения значений признака отдельных единиц совокупности. Полученная величина называется объемом признака. Расчетные показатели вычисляются по различным формулам и используются при анализе социально-экономических явлений.

Статистические показатели по временному фактору делятся на:

• Моментные показатели — отражают состояние или уровень явления на определенный момент времени. Например, число вкладов в Сбербанке на конец какого-либо периода.
• Интервальные показатели — характеризуют итоговый результат за период (день, неделя, месяц, квартал, год) в целом. Например, объем произведенной продукции за год.

Статистические показатели связаны между собой. Поэтому, чтообы составить целостное представление об изучаемом явлении или процессе, необходимо рассматривать систему показателей.

Абсолютная величина

Статистика измеряет и выражает явления общественной жизни с помощью количественных категорий — статистических величин. Результаты статистического наблюдения получают прежде всего в форме абсолютных величин, которые служат основой для расчета и анализа статистических показателей на следующих этапах статистического исследования.

Абсолютная величина — объем или размер изучаемого события или явления, процесса, выраженного в соответствующих единицах измерения в конкретных условиях места и времени.

Виды абсолютных величин:

• Индивидуальная абсолютная величина — характеризует единицу совокупности
• Суммарная абсолютная величина — характеризует группу единиц или всю совокупность

Результатом статистического наблюдения являются показатели, которые характеризуют абсолютные размеры или свойства изучаемого явления у каждой единицы наблюдения. Они называются индивидуальными абсолютными показателями. Если показатели характеризуют всю совокупность в целом, они называются обобщающими абсолютными показателями. Статистические показатели в форме абсолютных величин всегда имеют единицы измерения: натуральные или стоимостные.

Формы учета абсолютных величин:

• Натуральный — физические единицы (штук, человек)
• Условно-натуральный — применяется при подсчете итогов по продукции одинакового потребительского качества но широкого ассортимента. Перевод в условное измерение осуществляется с помощью коэффициента пересчета:
  К_{пересчета}=фактическое потребительское качество / эталон (заранее заданное качество)
• Стоимостной учет — денежные единицы

Натуральные единицы измерения бывают простыми, составными и условными.

Простые натуральные единицы измерения — это тонны, километры, штуки, литры, мили, дюймы и т. д. В простых натуральных единицах также измеряется объем статистической совокупности, т. е. число составляющих ее единиц, или объем отдельной ее части.

Составные натуральные единицы измерения имеют расчетные показатели, получаемые как произведение двух или нескольких показателей, имеющих простые единицы измерения. Например, учет затрат труда на предприятиях выражается в отработанных человеко-днях (число работников предприятия умножается на количество отработанных за период дней) или человеко-часах (число работников предприятия умножается на среднюю продолжительность одного рабочего дня и на количество рабочих дней в периоде); грузооборот транспорта выражается в тонно-километрах (масса перевезенного груза умножается на расстояние перевозки) и т. д.

Условно-натуральные единицы измерения широко используют в анализе производственной деятельности, когда требуется найти итоговое значение однотипных показателей, которые напрямую несопоставимы, но характеризуют одни и те же свойства объекта.

Натуральные единицы пересчитываются в условно-натуральные путем выражения разновидностей явления в единицах какого-либо эталона.

Например:

• различные виды органического топлива переводятся в условное топливо с теплотой сгорания 29,3 МДж/ кг
• мыло разных сортов — в условное мыло с 40%-ным содержанием жирных кислот
• консервы различного объема — в условные консервные банки объемом 353,4 см3,
• для подсчета общего объема работы транспорта складывают тонно-километры перевезенных грузов и пассажиро-километры, произведенные пассажирским транспортом, условно приравнивая при этом перевозку одного пассажира к перевозке одной тонны груза и т. д.

Перевод в условные единицы осуществляется с помощью специальных коэффициентов. Например, если имеется 200 т мыла с содержанием жирных кислот 40% и 100 т с содержанием жирных кислот 60%, то в пересчете на 40%-ное, получим общий объем 350 т условного мыла (коэффициент пересчета определяется как отношение 60: 40 = 1,5 и, следовательно, 100 т · 1,5 = 150 т условного мыла).

Пример 1

Найти условно-натуральную величину:

Допустим мы производим тетради:

• по 12 листов — 1000 шт;
• по 24 листа — 200 шт;
• по 48 листов — 50 шт;
• по 96 листов — 100 шт.

Решение:
Задаем эталон — 12 листов.
Считаем коэффициент пересчета:

• 12/12=1
• 24/12=2
• 48/12=4
• 96/12=8

Ответ: Условно натуральная величина =1000*1 + 200*2 + 50*4 + 100*8 = 2400 тетрадей по 12 листов

В условиях рыночной экономики наибольшее значение и применение имеют стоимостные единицы измерения: рубли, доллары, евро, условные денежные единицы и др. Для оценки социально-экономических явлений и процессов используются показатели в текущих или фактически действующих ценах или в сопоставимых ценах.

Сама по себе абсолютная величина не дает полного представления об изучаемом явлении, не показывает его структуру, соотношение между отдельными частями, развитие во времени. В ней не выявлены соотношения с другими абсолютными величинами. Поэтому статистика, не ограничиваясь абсолютными величинами, широко использует общенаучные методы сравнения, обобщения.

Абсолютные величины имеют большое научное и практическое значение. Они характеризуют наличие тех или иных ресурсов и являются основой разнообразных относительных показателей.

Относительные величины

Наряду с абсолютными величинами в экономическом анализе и экономической статистике используются также различные относительные величины. Относительные величины представляют собой различные коэффициенты или проценты.

Относительные статистические величины — это показатели, которые дают числовую меру соотношения двух сопоставляемых между собой величин.

Основное условие правильного расчета относительных величин — сопоставимость сравниваемых величин и наличие реальных связей между изучаемыми явлениями.

Относительная величина = сравниваемая величина / базис

• Величина, находящаяся в числителе соотношения, называется текущей или сравниваемой.
• Величина, находящаяся в знаменателе соотношения, называется основанием или базой сравнения.

По способу получения относительные величины — это всегда всегда величины производные (вторичные).

Они могут быть выражены:

• в коэффициентах, если база сравнения принимается за единицу (АбсВеличина / Базис) * 1
• в процентах, если база сравнения принимается за 100 (АбсВеличина / Базис) * 100
• в промилле, если база сравнения принимается за 1000 (АбсВеличина / Базис) * 1000
  Например показатель рождаемости в форме относительной величины, исчисляемый в промилле показывает число родившихся за год в расчете на 1000 человек.
• в продецимилле, если база сравнения принимается за 10000 (АбсВеличина / Базис) * 10000

Различают следующие виды относительных статистических величин:

• Относительная величина динамики
• Относительная величина планового задания
• Относительная величина выполнения плана
• Относительная величина структуры
• Относительная величина координации
• Относительная величина интенсивности
• Относительная величина сравнения