
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициенты корреляции зависимости от типов измерительных шкалСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изучение связи между признаками, которые принимают случайные значения, начинается с оценки его линейности Линейная корреляция Линейный корреляционная связь для эмпирических данных, измеренных по шкале интервалов или отношений, оценивается с помощью коэффициента корреляции Пирсона г ху где Хи и в и - значения переменных X и Y; х и у - средние X и Y; п - объем выборки 8 Указанные методы расчета с использованием компьютерной техники можно найти в учебнике [56]
Формула (222) может быть преобразована, если заменить значение переменных Х и и в и нормированными значениями 2х и гу, и выглядеть так:
Пример 27 Оценить связь между переменными X и У по эмпирическим данным таблицы рис 252 двумя способами с использованием формул (222) и (223) Способ 1 Последовательность решения: o оценить характер линейности связи между признаками X и В с помощью диаграммы рассеяния (рис 252);
Рис 252 Диаграмма рассеяния признаков o убедиться, что корреляция линейная и продолжить расчеты коэффициента корреляции Пирсона г ху (рис 253 и 254); o в ячейках В16 и С16 рассчитать средние значения х и у х = и хі = 112,00; У =1 ул = 18,17; o в ячейках и В15 рассчитать суммы квадратов разностей: X (х, - X)2 = 386,00; у, - у)2 = 311,67;
Рис 253 Результаты расчета коэффициента корреляции г ху o в ячейке Н18 рассчитать сумму произведений разниц: X (хі - X) o (уі - у) = 242,00; o в ячейке В17 рассчитать коэффициент корреляции г ху по формуле: гху = - 242,00 - 0,70 л/386, 00 o 311,67
Рис 254 Расчетные формулы Значение г ху ~ 0,70 свидетельствует о существенном прямая связь между признаками
Способ 2 Последовательность решения: o Результаты расчета г ху за нормируемыми данным показано на рис 255, расчетные формулы рис 256
Рис 255 Результаты расчета г ху за нормируемыми данным o в ячейках В16 и С16 рассчитать средние значения х и у; o в ячейках В17 и С17 рассчитать стандартные отклонения ух и уу;
Рис 256 Формулы расчета г ху за нормируемыми данным o в столбцах Б и Е рассчитать нормированные данные 2х и 2у (обратите внимание что среднее нормированных данных равен 0, а стандартное отклонение - 1,00); o в ячейке В18 рассчитать коэффициент корреляции r xy по формуле (223); Выводы Одно и то же значение r xy ~ 0,70 рассчитан двумя способами Методы расчета за нормируемыми данным выглядят более лаконично Значение парного коэффициента корреляции Пирсона r xy можно получить с помощью специальной функции MS Excel = Пирсон ()
36.Проверка адекватности однофакторной регрессионной модели. Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным. Адекватность регрессионной модели при малой выборе можно оценить F критерием Фишера:
где m – число параметров модели; n - число единиц наблюдения;
Эмпирическое значение критерия Если Проведем оценку адекватности регрессионной модели
Табличное значение Fт с уровнем значимости 0,05 и числом степеней свободы (2-1), (15-2) равно 4,68. (См. Приложение 7). Так как
При численности объектов анализа до 30 единиц (при малой выборе) возникает необходимость испытания параметров уравнения на их типичность (значимость). При этом осуществляется проверка, насколько вычисленные параметры характерны для отображаемого комплекса условий, не являются ли полученные значения параметров результатами действия случайных причин. Для проверки значимости параметров уравнения регрессии используется t – критерий Стьюдента. Вычисляются фактические значения t критерия: Для параметра
для параметра
где
Полученные фактические значения Параметр признается значимым (типичным), если эмпирическое значение
Оценим значимость параметров уравнения регрессии
Табличное значение t – критерия с уровнем значимости 0,05 и числом степеней свободы k=n-2=15-2=13 равно 2,161 (Приложение 6). Сравним фактические значения
Следовательно, вычисленные по уравнению регрессии параметры Измерение тесноты корреляционной связи. Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у.
Теснота связи между двумя признаками может измеряться линейным коэффициентов корреляции (r), корреляционным отношением ( Линейный коэффициент корреляции определяется по формулам:
или
Линейный коэффициент корреляции характеризует степень тесноты только при прямолинейной корреляционной зависимости. С коэффициентом регрессии Величина Квадрат линейного коэффициента корреляции Линейный коэффициент корреляции предложили в конце XIX века английские ученые Ф. Гальтон и К. Пирсон. При наличии криволинейной корреляционной связи Теоретическое корреляционное отношение ( Теоретическое корреляционное отношение определяется по формулам:
Корреляционное отношение в квадрате Для упрощения расчетов степени тесноты связи часто применяется индекс корреляции. Индекс корреляции определяется по следующим формулам:
Абсолютные размеры линейного коэффициента корреляции, корреляционного отношения, индекса корреляции колеблются от 0 до 1. Направление связи (знак перед Для качественной оценки тесноты связи можно воспользоваться также шкалой Чеддока:
Показатели При выборе вида уравнения можно воспользоваться еще критерием криволинейности Используем данные табл. 7.7 и рассчитаем линейный коэффициент корреляции, теоретическое корреляционное отношение и индекс корреляции:
Все показатели тесноты корреляционной связи показывают весьма высокую связь между объемами привлеченных и собственных средств. Коэффициент детерминации 0,947 означает, что вариация привлеченных средств банков на 94,7% объясняется вариацией собственных средств и на 5,7% - прочими факторами. Так как
37.Трехмерная (двухфакторная) линейная модель линейной корреляционной связи. 38.Парные и частные коэффициенты корреляции, совокупный коэффициент множественной корреляции и детерминации. Если факторные признаки различны по своей сущности и/или имеют различные единицы измерения, то коэффициенты регрессии при разных факторах являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы. К ним относят: частные коэффициенты эластичности, β -коэффициенты, частные коэффициенты корреляции. Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.
где - среднее квадратическое отклонение факторного признака; - среднее квадратическое отклонение результативного признака. Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели. Для качественной оценки тесноты связи можно использовать следующую классификацию: 0.1- 0.3- слабая связь 0.3-0.5 – умеренная связь 0.5-0.7- заметная связь 0.7-0.9- тесная связь 0.9-0.99- весьма тесная Для расчета частных коэффициентов корреляции могут быть использованы парные коэффициенты корреляции. Для случая зависимости Yот двух факторов можно вычислить 2 коэффициента частной корреляции:
(2-ой фактор фиксирован);
(1-ый фактор фиксирован).
Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых на результат устраняется). Частные коэффициенты корреляции, рассчитанные по таким формулам изменяются от -1 до +1. Они используются не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях нет смысла вводить в уравнение m -ый фактор, т.к. качество уравнения регрессии при его введении возрастет незначительно (т.е. теоретический коэффициент детерминации увеличится незначительно). Совокупный коэффициент множественной корреляции или индекс множественной корреляции определяет тесноту совместного влияния факторов на результат:
где остаточная дисперсия; или . Он принимает значения от 0 до 1 (в отличие от парного коэффициента корреляции, который может принимать отрицательные значения, R используется без учета направления связи). Чем плотнее фактические значения располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина. Таким образом, при значении R близком к 1, уравнение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат; при значении R близком к 0 уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат. При трех переменных для двух факторного уравнения регрессии данная формула совокупного коэффициента множественной корреляции легко приводится к следующему виду:
Чем R ближе к единице, тем совокупное влияние изучаемых показателей x1 и x2 на результативный фактор y больше (корреляционная связь более интенсивная). Множественный (совокупный) коэффициент детерминации определим как квадрат множественного коэффициента корреляции. Показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии. Его значение - в пределах от нуля до единицы. Чем ближе множественный коэффициент детерминации к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов.
Связь: Частный коэффициент корреляции в отличие от коэффициента (полного) парной корреляции между явлениями показывает тесноту связи после устранения изменений, обусловленных влиянием третьего явления на оба коррелируемых признака (из значений корреляционных признаков вычитаются линейные оценки в связи с третьим признаком). Также из приведенных ранее формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле:
При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице. Из единицы вычитается доля остаточной дисперсии результативного признака, обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.
39.Непараметрические методы установления связи между качественными признаками. Методы корреляционного и регрессионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. Между тем в статистике приходиться сталкиваться с задачами измерения связи между качественными признаками. Такие методы измерения связи называются непараметрические. Для исследования степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, может быть использован коэффициент ассоциации Д. Юла или коэффициент контингенции К. Пирсона. Расчетная таблица в этом случае состоит из четырех ячеек (таблица «четырех полей») и имеет следующий вид:
Коэффициент ассоциации вычисляется по формуле:
Коэффициент контингенции:
Если по каждому из взаимосвязанных признаков выделяется число групп более двух то для подобного таблиц теснота связи между качественными признаками может быть измерена с помощью коэффициентов взаимной сопряженности К. Пирсона и А. А. Чупрова. Коэффициент взаимной сопряженности Пирсона вычисляется по формуле:
Коэффициент Чупрова:
Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что значение этих признаков могут быть проранжированы по степени убывания или возрастания, используется коэффициент корреляции рангов Спирмена:
где d – разность рангов признаков x и y; n - число наблюдаемых единиц. В случае отсутствия связи r = 0. При прямой связи коэффициент r - положительная правильная дробь, при обратной – отрицательная. Если объём исходной информации небольшой, то необходимо выполнить проверку существенности рангового коэффициента, т. е. сверить с таблицей предельных значений. Расчетное значение r должно быть больше предельного. Для определения тесноты связи между произвольным числом ранжированных признаков применяется коэффициент конкордации:
где m – количество факторов; n - число наблюдений; S - отклонение суммы квадратов рангов от средней квадратов рангов. Рассмотрим пример: В результате обследования студентов факультета получены следующие данные:
Определите коэффициент ассоциации и контингенции между успеваемостью и посещаемостью спортивных секций. Коэффициент ассоциации:
Коэффициент контингенции:
Полученные коэффициенты подтверждают наличие существенной связи между исследуемыми признаками. Однако коэффициент контингенции всегда меньше коэффициента ассоциации и дает более корректную оценку тесноту связи.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1074; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.125 (0.015 с.) |

 ,
, - факторная дисперсия, которая характеризует вариацию результативного признака под влиянием признака фактора, включенного в модель;
- факторная дисперсия, которая характеризует вариацию результативного признака под влиянием признака фактора, включенного в модель; - остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих, неучтенных факторов;
- остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих, неучтенных факторов; - общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию:
- общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию: .
. сравнивается с критическим (табличным)
сравнивается с критическим (табличным)  с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m-1), (n-m).
с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m-1), (n-m). , выражающей зависимость среднего объема привлеченных средств банков от собственных средств, с помощью F критерия Фишера:
, выражающей зависимость среднего объема привлеченных средств банков от собственных средств, с помощью F критерия Фишера: ;
; ;
; ;
; .
. , то уравнение регрессии можно признать адекватным.
, то уравнение регрессии можно признать адекватным. :
: ;
; :
: ,
, - среднее квадратическое отклонение результативного признака от выравненных значений
- среднее квадратическое отклонение результативного признака от выравненных значений  ;
;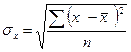 - среднее квадратическое отклонение факторного признака хот общей средней
- среднее квадратическое отклонение факторного признака хот общей средней  .
. и
и  сравниваются с критическим
сравниваются с критическим  , который получают по таблице Стьюдента с учетом принятого уровня значимости а (а =0,01 или а =0,05) и числа степеней свободы k=n-2.
, который получают по таблице Стьюдента с учетом принятого уровня значимости а (а =0,01 или а =0,05) и числа степеней свободы k=n-2. больше критического табличного
больше критического табличного  ;
; ;
; ;
; .
. ) и индексом корреляции (R).
) и индексом корреляции (R).
 .
. .
. принимает значения в интервале:
принимает значения в интервале:  . Отрицательные значения указывают на обратную связь, положительные – на прямую. При
. Отрицательные значения указывают на обратную связь, положительные – на прямую. При  , связь функциональная.
, связь функциональная.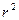 называется линейным коэффициентом детерминации, показывает удельный вес влияния данного фактора в общей сумме всех факторов, определяющих уровень результативного признака.
называется линейным коэффициентом детерминации, показывает удельный вес влияния данного фактора в общей сумме всех факторов, определяющих уровень результативного признака. ) служат для измерения тесноты связи как при прямолинейной, так и при криволинейной корреляционной связи.
) служат для измерения тесноты связи как при прямолинейной, так и при криволинейной корреляционной связи. или
или 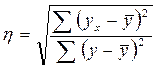 .
. показывает, какую часть всей вариации результативного признака составляет вариация, вызванная факторным признаком.
показывает, какую часть всей вариации результативного признака составляет вариация, вызванная факторным признаком. или
или  .
. не превышает 0,1, предположение о прямолинейной форме корреляционной связи можно считать оправданным.
не превышает 0,1, предположение о прямолинейной форме корреляционной связи можно считать оправданным. , если k> 2,5, то предположение о данном виде криволинейной связи можно считать оправданным.
, если k> 2,5, то предположение о данном виде криволинейной связи можно считать оправданным. ;
; ;
; ;
; ;
; .
. , то можно седлать заключение, что гипотеза о линейной форме связи подтверждена.
, то можно седлать заключение, что гипотеза о линейной форме связи подтверждена. (нет)
(нет)
 (нет)
(нет)
 .
. .
. , где j2 – показатель средней квадратической сопряженности, который вычисляется по формуле:
, где j2 – показатель средней квадратической сопряженности, который вычисляется по формуле: , где
, где  ,
,  .
. , где К1, К2 – число групп по каждому из признаков.
, где К1, К2 – число групп по каждому из признаков. ,
, ,
,
 .
.


