
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Корреляционно-регрессионныйСодержание книги Поиск на нашем сайте
АНАЛИЗ. НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ АНАЛИЗА СВЯЗИ
4.1 Методические указания и примеры решения задач
Все социально-экономические явления взаимосвязаны. Связь между ними носит причинно-следственный характер. Признаки, характеризующие причины и условия связи, называются факторными (х), а те, которые характеризуют последствия связи, - результативными (у). Между признаками х и у возникают разные по природе и характеру связи, в частности функциональные и стохастические. При функциональной связи каждому значению признака х отвечает одно четко определенное значение у. Эта связь проявляется однозначно в каждом конкретном случае. При стохастической связи каждому значению признака х отвечает определенное множество значений у, которые образовывают так называемое условное распределение. Как закон эта связь проявляется только в массе случаев и характеризуется изменением условных распределений у. Если заменить условные распределения средней величиной у, то образуется разновидность стохастической связи – корреляционная. В случае корреляционной связи каждому значению признака х отвечает среднее значение результативного признака у. Примером стохастической и, в частности, корреляционной связи является распределение проданных на бирже недвижимости однокомнатных квартир по их стоимости у и размеру общей площади х (табл. 4.1).
Таблица 4.1 Распределение проданных на бирже недвижимости однокомнатных квартир по их стоимости и размеру на 1.01.2010 г.
Каждой группе по факторному признаку отвечает свое распределение у, которое отличается от других групп и от безусловного итогового распределения. Следовательно, наблюдается стохастическая связь между признаками. Условные распределения можно заменить средними значениями результативного признака, которые вычисляют как среднюю арифметическую взвешенную. Постепенное изменение средних Характеристикой корреляционной связи является линия регрессии, которую рассматривают в двух моделях - аналитической группировки и регрессионного анализа. В модели аналитической группировки это эмпирическая линия регрессии, которая образовывается из групповых средних значений результативного признака Эффекты воздействия х на у определяют как отношение приростов средних групповых значений:
Пример1. По данным таблицы 4.1 приросты
Следовательно, с увеличением размера общей площади квартир на 1 м² их стоимость в среднем растет соответственно на:
Оценка плотности связи основывается на правиле сложения дисперсий. В модели аналитической группировки мерой плотности связи выступает отношение межгрупповой дисперсии к общей, которое называется корреляционным отношением:
где
Корреляционное отношение колеблется от нуля до единицы, а если выразить в процентах, то от 0 до 100 %. При отсутствии связи Пример2. По данным таблицы 4.1 общая дисперсия стоимости проданных квартир будет равна:
В таблице 4.2 приведена аналитическая группировка проданных квартир, которая описывает зависимость их стоимости от общей площади. Там же дан расчет межгрупповой дисперсии.
Таблица 4.2 Аналитическая группировка проданных на бирже квартир
Корреляционное отношение
следовательно, вариация стоимости проданных квартир на 66 % объясняется вариацией их общей площади и на 34 % - вариацией других факторов, т.е. связь между признаками достаточно плотная. Однако плотная связь может возникнуть случайно, поэтому необходимо проверить ее тесноту, т.е. доказать неслучайность связи. Проверка тесноты связи – это сравнение фактического значения В нашем примере Поскольку В модели регрессивного анализа характеристикой корреляционной связи является теоретическая линия регрессии, описываемая функцией - линейные уравнения - нелинейные уравнения, когда изменение взаимосвязанных признаков происходит неравномерно (с ускорением, замедлением или с переменным направлением связи), в частности: степенное Чаще применяют линейные уравнения или приведенные к линейному виду. В линейном уравнении параметр b - коэффициент регрессии указывает, на сколько единиц в среднем изменится у с изменением х на единицу. Он имеет единицу измерения результативного признака. В случае прямой связи b – величина положительная, а при обратной - отрицательная. Параметр a – свободный член уравнения регрессии, т.е. это значение Y при х = 0. Если х не приобретает нулевые значения, то данный параметр имеет только расчетное значение. Параметры определяются методом наименьших квадратов, согласно которому сумма квадратов отклонений эмпирических значений у от Y минимальна:
Отсюда
Для расчета параметров уравнения параболы второго порядка методом наименьших квадратов система нормальных уравнений имеет следующий вид:
Коэффициент регрессии в небольших по объему совокупностях подвержен случайным колебаниям. Поэтому проверяют его существенность с помощью t критерия (Стьюдента):
где b – коэффициент регрессии;
где n – объем совокупности. Характеристикой относительного изменения у вследствие изменения х есть коэффициент эластичности:
который показывает, на сколько процентов в среднем меняется результативный признак с изменением факторного на 1 %. На основании уравнения регрессии определяют теоретические значения Y, т.е. значение результативного признака при условии воздействия только фактора х при неизменном уровне других факторов. Отклонения эмпирических значений у от теоретических Y называют остаточными. Они характеризуют воздействие на результативный признак всех других факторов, кроме х. Средний размер этих отклонений определяет остаточная дисперсия
Вариацию у, обусловленную воздействием только фактора х, называют факторной дисперсией:
Доля факторной дисперсии в общей характеризует плотность связи и называется коэффициентом детерминации:
Он имеет такой же смысл, интерпретацию и цифровые границы, что и Плотность связи оценивается также индексом корреляции
который принимает значения в границах Абсолютное значение r равно индексу корреляции:
Однако для интерпретации r необходимо перейти к уравнению Проверка существенности связи в обеих моделях может определяться также по критерию Фишера, который функционально связан с
или
поэтому процедура проверки и выводы идентичны. Наряду с относительно точными и сложными корреляционными измерениями имеются и менее точные, но распространенные методы установления взаимосвязей между изучаемыми статистическими рядами. Коэффициент Фехнера рассчитывается на основе сравнения параллельных рядов. С его помощью можно установить направление связи и ее тесноту. Вначале исчисляется средняя арифметическая ряда признака-фактора ( Коэффициент Фехнера будет вычисляться по формуле:
где КФ - коэффициент Фехнера; С - число совпадений знаков; Н - число несовпадений знаков. Коэффициент Фехнера изменяется от +1 до -1. При +1 имеется полная прямая согласованность, при 0 - изменчивость никак не согласуется, при -1 - полная обратная несогласованность. Часто в статистике для установления связи находят применение коэффициенты ранговой корреляции Спирмена и Кендалла. Коэффициент Спирмена рассчитывается по формуле:
где r - коэффициент Спирмена; d2 - квадрат разности рангов; n - число сопоставляемых пар рангов; 1 и 6 - постоянные коэффициенты. Методика расчета коэффициента ранговой корреляции Кендаллааналогична методике расчета коэффициента Спирмена, только с иным расчетом суммы рангов. Это, прежде всего, касается ряда значений результативного признака. Коэффициент ранговой корреляции Кендалла рассчитывается по следующей формуле:
где t - коэффициент ранговой корреляции Кендалла; S - сумма разности между значениями; n - число сопоставляемых рангов; 1/2 и 1 - постоянные коэффициенты. Коэффициенты Кендалла и Спирмена изменяются от +1 до -1. Для измерения связи между качественными ( атрибутивными) признаками в статистике широко используются коэффициент сопряженности А.А. Чупрова и коэффициент ассоциации К. Пирсона. Коэффициент ассоциации К. Пирсона в плане исчисления - относительно простой показатель сопряженности величин. Он применяется к вариации двух качественных признаков, распределенных по двум группам.Его расчет производится на основе таблицы 4.3, именуемой таблицей четырех полей.
Таблица 4.3
Этими полями являются клетки а, b, с, d. Расчет осуществляется на основе сопряжения по строкам а и b, с и d, а также по графам а и с, b u d. Коэффициент ассоциации Пирсона определяется по формуле:
Ассоциируемые показатели могут быть как абсолютными, так и относительными. Коэффициент ассоциации измеряется от -1 до +1 и интерпретируется так: чем ближе коэффициент к 1, тем теснее связь, положительная или отрицательная. Коэффициент взаимной сопряженностиА.А. Чупрова, в отличие от коэффициента Пирсона, применяется для измерения связи между соотношением двух атрибутивных признаков по трем и более группам. Он рассчитывается по формуле:
где КЧ - коэффициент взаимной сопряженности А.А. Чупрова; j 2 - показатель взаимного сопряжения; m1 и m2 - число групп по каждому признаку; 1 - постоянный коэффициент. Коэффициент A.A. Чупрова варьирует от 0 до 1 и его значение не может быть отрицательным. Связь считается существенной при величине коэффициента равной 0,3. Чем ближе его значение к единице, тем сильнее связь. Пример 3. Основываясь на данных табл. 4.4, с помощью метода параллельных рядов необходимо установить наличие и характер связи между преступностью несовершеннолетних и наркоманией.
Таблица 4.4
Приведенные в табл. 4.4 данные свидетельствуют о том, как изменилась в стране ситуация, связанная с правонарушениями на почве наркомании подростков. В 1996 - 2000 гг. число подростков, состоящих на учете в ОВД за немедицинское потребление наркотиков, возросло в 5,5 раза (с 4,6 до 25,5 тыс. человек), в 2,2 раза увеличилось число лиц, совершивших преступления в состоянии наркотического возбуждения (с 0,5 до 1,1 тыс. человек). Как следствие этого, за анализируемый период число преступлений, совершенных подростками и связанных с приобретением, хранением, перевозкой или сбытом наркотических средств, выросло в 2,8 раза (с 2,0 до 5,5 тыс.). Таким образом, с увеличением числа подростков-наркоманов, состоящих на учете и несовершеннолетних, совершивших преступления в состоянии наркотического возбуждения, происходит рост числа преступлений, связанных с незаконным изготовлением, хранением, перевозкой наркотиков, совершаемых подростками. На лицо прямая связь между преступностью несовершеннолетних и наркоманией.
4.2 Задачи для самостоятельного выполнения
Задача 1. Имеются следующие данные о распределении рабочих бригады по выработке и стажу работы:
Таблица 4.5 Распределение рабочих бригады по выработке и стажу работы
С целью определения формы корреляционной зависимости между производительностью труда и стажем работы на основе ранжированных данных о производительности труда и стаже работы двадцати рабочих бригады, представленных в таблице, необходимо: 1) установить результативный и факторный признаки; 2) определить наличие и форму корреляционной связи между производительностью труда рабочих бригады и стажем работы, используя: а) метод сопоставления параллельных рядов; б) метод групповой таблицы. Результаты группировки представить в таблице; в) графический метод. Построить поле корреляции и эмпирическую линию связи. 3) проанализировать полученный результат. Задача 2. С целью изучения взаимосвязи между производительностью труда и стажем работы на основе ранжированных данных о производительности труда и стаже работы двадцати рабочих бригады, представленных в таблице 4.5, и результатов решения задачи 1 необходимо: 1) построить регрессионную модель парной корреляционной зависимости и определить её параметры; 2) построить на графике теоретическую кривую корреляционной зависимости; 3) рассчитать показатели тесноты связи между выработкой рабочего и стажем работы. Дать качественную оценку степени тесноты связи; 4) оценить существенность параметров регрессивной модели и показателей тесноты связи. Дать оценку надёжности уравнения регрессии; 5) дать экспериментальную интерпретацию параметров построенной регрессионной модели. Задача 3. Имеются следующие данные о промышленных предприятиях, производящих один вид продукции (таблица 4.6). Для характеристики связи между рассматриваемыми показателями определите: 1) уравнение парной регрессии между электоровооруженностью и производительностью труда; 2) коэффициент парной корреляции; 3) среднюю ошибку коэффициента корреляции; 4) коэффициент детерминации; 5) коэффициент эластичности; 6) проверьте существенность связи с учетом уровня значимости 0,05; 7) постройте график эмпирической и теоретической зависимости. Проанализируйте полученный результат.
Таблица 4.6 Показатели электоровооруженности и производительности труда промышленных предприятий
Задача 4. Имеются следующие данные о производстве промышленной продукции предприятиями региона (таблица 4.7).
Таблица 4.7 Выполнение плана по выпуску продукции и производительность труда промышленных предприятий региона
С целью анализа степени тесноты связи между выполнением плана по выпуску продукции и производительностью труда необходимо: 1) определить факторный и результативный показатели; 2) рассчитать коэффициент парной корреляции между результативным и факторным показателями; 3) провести оценку существенности коэффициента парной корреляции, если табличное значение t-критерия Стьюдента равно 2,228; 4) дать качественную оценку степени тесноты связи между показателями; 5) рассчитать коэффициент парной детерминации и проанализируйте его значение. Задача 5. На основании данных задачи 4 с целью анализа взаимосвязи между выполнением плана по выпуску продукции и производительностью труда необходимо: 1) построить регрессионную модель парной корреляционной зависимости и определить её параметры; 2) построить на графике теоретическую кривую корреляционной зависимости; 3) оценить существенность параметров регрессивной модели. Дать оценку надёжности уравнения регрессии; 4) дать экспериментальную интерпретацию параметров построенной регрессионной модели. Задача 6. Имеются следующие данные по группе предприятий отрасли промышленности о фондоотдаче на один рубль основных промышленно-производственных фондов и долю активной их части (таблица 4.8). Определите параметры линейного уравнения регрессии, характеризующего зависимость уровня фондоотдачи от доли активной части основных промышленно-производственных фондов, дайте им экономическую интерпретацию. С помощью коэффициента детерминации измерьте тесноту связи: проверьте ее существенность с уровнем значимости 0,05.
Таблица 4.8 Показатели фондоотдачи предприятий
Задача 7. Известно следующее распределение 70 рабочих промышленного предприятия по степени удовлетворенности условиями труда на рабочем месте и своей профессией:
Таблица 4.9 Распределение рабочих предприятия по степени удовлетворенности условиями труда и своей профессией
Оцените тесноту связи с помощью коэффициента ассоциации и коэффициента взаимной сопряженности между удовлетворенностью рабочих условиями труда и удовлетворенностью своей профессией. Проверьте существенность связи с уровнем значимости 0,05. Задача 8. По данным социологического обследования получено следующее распределение 400 рабочих по уровню удовлетворенности своей работой и по ответам на вопрос о потенциальной текучести (таблица 4.10).
Таблица 4.10 Результаты социологического обследования рабочих
Оцените с помощью коэффициента взаимной сопряженности тесноту связи между удовлетворенностью рабочих своей работой и степенью их потенциальной текучести. Проверьте существенность связи с уровнем значимости 0,05. Задача 9. В таблице 4.11 представлены данные о распределении погибших и раненых по вине водителей и пешеходов за текущий год.
Таблица 4.11 Распределении погибших и раненых по вине водителей и пешеходов
По данным таблицы 4.11 определить коэффициент ассоциации Пирсона и установить направление и тесноту связи между ранеными и погибшими в дорожно-транспортных происшествиях по вине водителей и пешеходов. Задача 10. Используя данные таблицы 4.12, определить зависимость между предпочтением в выборе профессий у 358-ми опрошенных детей и профессиями их родителей. Рассчитать коэффициент тесноты связи (коэффициент Пирсона). Сделать выводы. Таблица 4.12
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.186.153 (0.009 с.) |



 от одной группы к другой свидетельствует о наличии корреляционной связи между признаками.
от одной группы к другой свидетельствует о наличии корреляционной связи между признаками. для каждого значения (интервала)
для каждого значения (интервала)  .
. , где
, где 
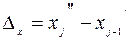 .
.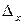 во всех группах одинаковы – 5 м², а средняя стоимость проданных квартир увеличивается по группам следующим образом:
во всех группах одинаковы – 5 м², а средняя стоимость проданных квартир увеличивается по группам следующим образом: тыс. усл. ед.;
тыс. усл. ед.; 

 тыс. усл. ед. и на 0,4 и 0,56.
тыс. усл. ед. и на 0,4 и 0,56. ,
, – общая дисперсия, которая измеряет вариацию результативного признака у, обусловленную воздействием всех возможных факторов;
– общая дисперсия, которая измеряет вариацию результативного признака у, обусловленную воздействием всех возможных факторов; – межгрупповая дисперсия, которая измеряет вариацию результативного признака у под воздействием только группировочного признака х.
– межгрупповая дисперсия, которая измеряет вариацию результативного признака у под воздействием только группировочного признака х. , а при условии функциональной связи
, а при условии функциональной связи  Чем больше
Чем больше  приближается к единице, тем более плотная связь.
приближается к единице, тем более плотная связь.
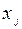 , м²
, м²



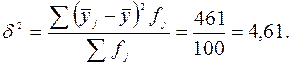

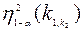 для определенного уровня тесноты α и числа степеней свободы
для определенного уровня тесноты α и числа степеней свободы  и
и  , где
, где 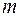 - число групп,
- число групп,  - объем совокупности. Если
- объем совокупности. Если  , то связь признается существенной. Критические значения корреляционного отношения для
, то связь признается существенной. Критические значения корреляционного отношения для  приведены в специальных таблицах.
приведены в специальных таблицах.
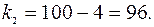 Из-за отсутствия в таблице критических значений
Из-за отсутствия в таблице критических значений  используем ближайшее (
используем ближайшее ( ), тогда
), тогда  .
. то связь признается существенной с вероятностью 0,95.
то связь признается существенной с вероятностью 0,95. которая называется уравнением регрессии. В зависимости от характера связи используют:
которая называется уравнением регрессии. В зависимости от характера связи используют: когда с изменением х признак у изменяется более или менее равномерно;
когда с изменением х признак у изменяется более или менее равномерно; гиперболическое
гиперболическое  параболическое
параболическое  и т.п.
и т.п. В соответствии с условием минимизации параметры линейного уравнения регрессии вычисляют на основании системы нормальных уравнений:
В соответствии с условием минимизации параметры линейного уравнения регрессии вычисляют на основании системы нормальных уравнений: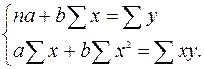




 - стандартная погрешность, которую рассчитывают по формуле:
- стандартная погрешность, которую рассчитывают по формуле:

 – соответственно остаточная и факторная дисперсии;
– соответственно остаточная и факторная дисперсии;
 .
.
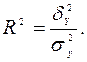

 , однако интерпретируется только
, однако интерпретируется только  Для линейной связи используют линейный коэффициент корреляции (Пирсона) r:
Для линейной связи используют линейный коэффициент корреляции (Пирсона) r: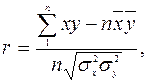
 , поэтому характеризует не только плотность, но и направление связи. Положительное значение свидетельствует о прямой связи, а отрицательное – об обратной.
, поэтому характеризует не только плотность, но и направление связи. Положительное значение свидетельствует о прямой связи, а отрицательное – об обратной.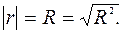
 Проверка существенности связи выполняется таким же образом, как и в модели аналитической группировки, путем сравнения
Проверка существенности связи выполняется таким же образом, как и в модели аналитической группировки, путем сравнения  и
и  Отличия касаются только определения
Отличия касаются только определения 
 , в которых m – число параметров уравнения регрессии.
, в которых m – число параметров уравнения регрессии. :
:

 ) и признака-следствия (
) и признака-следствия ( ). Затем определяются знаки отклонений от средних. Если реальное значение больше средней, то против него ставится знак (+), меньше - знак (-). Совпадение знаков по отдельным значениям ряда х и у означает согласованную вариацию, несовпадение - нарушение согласованности.
). Затем определяются знаки отклонений от средних. Если реальное значение больше средней, то против него ставится знак (+), меньше - знак (-). Совпадение знаков по отдельным значениям ряда х и у означает согласованную вариацию, несовпадение - нарушение согласованности. ,
,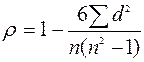 ,
, ,
,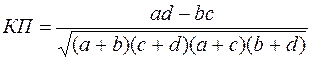 .
. ,
,


