
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Аналитические показатели рядаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ДИНАМИКИ И МЕТОДЫ ПРОГНОЗИРОВАНИЯ ИХ УРОВНЕЙ. АНАЛИЗ ТРЕНДА И СЕЗОННЫХ КОЛЕБАНИЙ
3.1 Методические указания и примеры решения задач
Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени. В статистике для выявления специфики развития изучаемых явлений за отдельные периоды времени определяют относительные и абсолютные показатели изменения ряда динамики: темпы роста, абсолютные и относительные приросты, абсолютное значение одного процента прироста. Пример 1. Выпуск продукции предприятием за 1993 – 1998 гг. характеризуется следующими данными (в сопоставимых ценах; млн. руб.): 1993 1994 1995 1996 1997 1998 12,3 13,4 14,8 16,4 17,8 19,9 Требуется произвести анализ динамики выпуска продукции предприятием за эти годы. Важнейшим показателем изменений абсолютных уровней ряда динамики по отдельным периодам времени является темп роста К. Величина этого показателя определяется из сопоставления уровня изучаемого периода yi с уровнем, который принимается за базу сравнения. Выражаются темпы роста в процентах или в виде коэффициентов. Выбор базы для расчета в ряду динамики темпов роста определяется задачей исследования. Если задачей изучения ряда динамики является, например, контроль хода выполнения данным производством пятилетнего плана, то сравнение уровней ряда динамики производится по отношению к году, который принимался за базу при разработке пятилетнего плана. В данном примере – это 1993 г., и расчет темпов роста будет производиться на постоянной базе сравнения, т.е. по схеме базисных темпов роста:
Определите базисные темпы роста: 1994 1995 1996 1997 1998 Из полученных базисных темпов роста следует, что по годам пятилетки происходило систематическое возрастание темпов роста выпуска продукции, %:
Если же при изучении данного ряда динамики ставится задача определить изменение выпуска продукции в каждом последующем периоде по сравнению с предыдущим (например, для контроля выполнения годовых планов), то определяются цепные (погодовые) темпы роста Кц, когда за базу сравнения отдельных уровней ряда yi каждый раз принимается предыдущий уровень yi-1:
Определим цепные темпы роста:
1994 1995 1996 1997 1998 Из полученных цепных темпов роста видно, что в 1994, 1995 и 1996 гг. происходил рост выпуска продукции из года в год, %:
В 1997 г. имело место некоторое промедление роста выпуска продукции, %:
Эта специфика развития данного явления в 1997 г. из определенных выше показателей базисных темпов роста не была видна. Для выражения изменений уровней ряда динамики в абсолютных величинах исчисляют статистический показатель абсолютного прироста ∆у. Величина этого показателя определяется как разность между уровнем изучаемого периода yi и уровнем, принимаемым за базу сравнения. При определении накопленных (базисных) абсолютных приростов ∆yб за базу сравнения принимается постоянный уровень. В рассматриваемом примере – это уровень 1993 г., и расчет накопленного (базисного) абсолютного прироста (млн. руб.) производится по формуле: ∆уб=yi-y0. 1994 13,4 – 12,3=1,1 1995 14,8 – 12,3=2,5 1996 16,4 – 12,3=4,1 1997 17,8 – 12,3=5,5 1998 19,9 – 12,3=7,6 Из полученных значений накопленных абсолютных приростов видно, что по годам пятилетки происходило систематическое возрастание абсолютных приростов выпуска продукции, млн. руб.: 1,1 < 2,5 < 4,1 < 5,5 < 7,6. При определении цепных абсолютных приростов ∆уц базой сравнения каждый раз выступает уровень предыдущего периода уi-1, и расчет абсолютных приростов (млн. руб.) производится по формуле ∆уц=уi – yi-1. Следовательно, 1994 13,4 – 12,3=1,1 1995 14,8 – 13,4=1,4 1996 16,4 – 14,8=1,6 1997 17,8 – 16,4=1,4 1998 19,9 – 17,8=2,1 Из полученных погодовых (цепных) абсолютных приростов видно сокращение абсолютного прироста выпуска продукции на данном предприятии в 1997 г., млн. руб.: 1,1 < 1,4 < 1,6 > 1,4 < 2,1. Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется статистический показатель – темп прироста ∆К. Величина темпа прироста ∆К определяется из сравнения в отношении абсолютного прироста ∆у с уровнем, принимаемом при анализе за базу сравнения. При исчислении базисных темпов прироста ∆Кб в качестве базы сравнения берется постоянный уровень у0. В рассматриваемом ряду динамики – это уровень 1993 г., и расчет базисных темпов прироста производится по формуле:
Определим базисные темпы прироста, %:
1994 1995 1996 1997 1998 Базисные темпы прироста, подобно базисным темпам роста, показывают систематическое возрастание по годам пятилетки выпуска продукции данным предприятием. Но в отличие от темпов роста, показывающих, во сколько раз (или процентов) происходит рост выпуска продукции, базисные темпы прироста показывают, на сколько произошло приращение (в относительных величинах) абсолютных уровней ряда динамики. При определении цепных темпов прироста ∆Кц в качестве базы сравнения выступает уровень предшествующего периода yi-1, и расчет осуществляется по формуле
Определяем эти показатели, %: 1994 1995 1996 1997 1998 Если же при определении темпов прироста ∆К предварительно были исчислены темпы роста К, то расчет темпов прироста производят так: ∆К=К – 1, или ∆К=К – 100% (если темп роста выражен в процентах). Например, для 1998 г. ∆Кц=Кц (1998 г.) – 1=1,118 – 1=0,118, или Кц (1998 г.) – 100=111,8% - 100%=11,8%; ∆Кб=Кб (1998 г.) – 1=1,618 – 1=0,618, или Кб (1998 г.) – 100=161,8% - 100%=61,8%. Показатель абсолютного значения одного процента прироста (А%) определяется путем отношения (в каждом периоде) абсолютного прироста ∆уц к темпу прироста ∆Кц. Расчет этого показателя имеет экономический смысл только на цепной основе:
Определим эти показатели, тыс. руб.: 1994 1995 1996 1997 1998 При анализе погодовых уровней ряда динамики расчет абсолютного значения одного процента прироста можно произвести по схеме: А%=0,01уi-1. Например, для 1997 г. А%=0,01 у (1996 г.) =0,01·16,4=0,164 млн. руб.; для 1998 г. А%=0,01 у (1997 г.) =0,01·17,8=0,178 млн. руб. Для суждения о среднем изменении абсолютных приростов исчисляется показатель среднего абсолютного прироста Обычно определение среднего абсолютного прироста производят по цепным абсолютным приростам ∆уц по формуле:
Так, для данного примера этот расчет будет следующим:
Средний абсолютный прирост можно исчислить и непосредственно по абсолютным уровням ряда динамики у по формуле:
где m – число учетных единиц времени в ряду динамики. Для данного примера имеем:
И наконец, в тех случаях, когда в качестве исходных материалов даны накопленные (базисные) абсолютные приросты ∆уб, то расчет среднего абсолютного прироста производится по формуле:
Для рассматриваемой задачи накопленный (базисный) абсолютный прирост равен 7,6 млн. руб. По этому значению расчет среднегодового абсолютного прироста составляет:
При изучении рядов динамики возникает необходимость определения среднего темпа роста явления за отдельные периоды его развития. Для рядов динамики годовых уровней чаще всего производят расчет среднегодовых темпов роста за отдельные этапы экономического развития страны (например, пятилетки). В рядах внутригодовой динамики исчисляют среднемесячные и среднегодовые темпы роста. Для определения среднего темпа роста обычно используют метод средней геометрической. Применительно к рядам динамики формула средней геометрической в общем виде записывается так:
где ПК – произведение цепных темпов роста (в коэффициентах); n- число К. В зависимости от характера исходных данных формула средней геометрической видоизменяется. Рассмотрим основные случаи определения средних темпов динамики: 1. Исчисление среднего темпа по цепным темпам роста.
Если в качестве исходных данных выступают цепные темпы роста, то для расчета среднего темпа динамики используется формула:
где К – цепные темпы роста (в коэффициентах); n – число темпов.
Пример 2. Выпуск продукции предприятием характеризуется следующими данными по кварталам 1998 г. в коэффициентах к предыдущему кварталу: 1 2 3 4 1,1095 1,240 1,2258 1,1974 Подставив в формулу
2. Расчет среднего темпа динамики по базисным темпам роста или прироста. Если в качестве исходных данных выступают базисные темпы роста или прироста, то на основе зависимости между цепными и базисными коэффициентами динамики расчет среднего темпа производят по формуле
где Кб – базисный темп роста (в коэффициентах); m – число учетных единиц времени в изучаемом периоде.
Пример 3. Планом экономического и социального развития производственного объединения на 1993 –1998 гг. предусматривается увеличение производства товарной продукции (в сопоставимых ценах) в 1,3 раза, в том числе товаров народного потребления – на 22%. Требуется определить, какие должны быть у объединения среднегодовые темпы роста производства товарной продукции. Заданный коэффициент (1,3) представляет темп развития производства товарной продукции в 1998 г. по сравнению с базой – 1993 годом, т.е. базисный темп роста:
Поэтому для определения среднегодового темпа применяется формула:
При m=6 (число годовых периодов в изучаемом отрезке времени):
Задание по росту выпуска товаров народного потребления выражено базисным темпом прироста. Для определения среднегодового темпа динамики заданный темп прироста (∆Кб=22%) необходимо из процентной формы выражения перевести в коэффициент (∆Кб=0,22) и далее в темп роста: Кб=∆Кб+1=0,22+1=1,22. Определим значение среднегодового темпа роста:
Пример 4. Планом экономического и социального развития города на 1994 – 1998 гг. предусмотрено достижение в 1994 г. объема розничного товарооборота государственной и кооперативной торговли 820 – 830 млн. руб. Требуется определить среднегодовые темпы роста объема розничного товарооборота города, если в 1993 г. объем розничного товарооборота государственной и кооперативной торговли города составил 590,4 млн. руб. Задание по росту объема товарооборота определено в форме абсолютных уровней, которые необходимо достигнуть в 1994 г. (уn=820 – 830). Для определения среднего темпа роста применяется формула:
При этом за базисный уровень принимается объем товарооборота области в 1993 г., т.е. года, который выступает в качестве базы при разработке плана.
При m=6 определяем: 1) для минимального значения конечного уровня:
2) для максимального значения конечного уровня:
3. Расчет среднего темпа динамики по средним уровням ряда. Если в качестве исходных данных выступают ряды динамики со значительными колебаниями уровней, то расчет среднего темпа динамики можно произвести по средним уровням ряда, исчисленным за отдельные периоды (этапы) развития явления. Важной задачей статистики при анализе рядов динамики является определение общей тенденции развития. На развитие явления во времени могут оказывать влияние различные по своему характеру и силе воздействия факторы. Одни из них оказывают более или менее постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным. При изучении в рядах динамики общей тенденции развития явления применяются различные приемы и методы. Одним из наиболее элементарных способов изучения общей тенденции в ряду динамики является укрупнение интервалов. Этот способ основан на укрупнении периодов, к которым относятся уровни ряда динамики. Пример 5. Имеются следующие данные о выпуске продукции группой предприятий по месяцам 1998 г., млн. руб.:
Таблица 3.1
Для выявления общей тенденции роста выпуска продукции произведем укрупнение интервалов. Для этой цели исходные (месячные) данные о выработке продукции объединяем в квартальные и получаем показатели выпуска продукции группой предприятий по кварталам 1998 г., млн. руб.:
Таблица 3.2
В результате укрупнения интервалов общая тенденция роста выпуска продукции данной группой заводов выступает отчетливо: 64,6 < 76,9 < 78,8 < 85,9. Выявление общей тенденции ряда динамики можно произвести путем сглаживания ряда динамики с помощью подвижной (скользящей) средней. Сущность этого приема состоит в том, что по исходным уровням ряда (эмпирическим данным) определяют расчетные (теоретические) уровни. При этом посредством осреднения эмпирических данных индивидуальные колебания погашаются, и общая тенденция развития явления выражается в виде некоторой плавной линии (теоретические уровни). При изучении общей тенденции методом аналитического выравнивания исходят из того, что изменение уровней ряда динамики могут быть с той или иной степенью приближения выражены определенными математическими функциями. На основе теоретического анализа выявляется характер развития явления во времени и на этой основе выбирается то или иное математическое выражение типа изменения явления: по прямой, параболе второго порядка, показательной (логарифмической) кривой и т.д. Рассмотрим применение метода аналитического выравнивания по прямой для выражения общей тенденции на следующем примере.
Пример 6. Имеются данные о выпуске продукции предприятиями легкой промышленности района за 1990 – 1998 гг. (в сопоставимых ценах, млн. руб.):
Таблица 3.3
Общее представление о характере тенденции изменения изучаемого явления можно получить из графического изображения ряда динамики (рисунок 3.1).
Рисунок 3.1 – Выпуск продукции предприятиями легкой промышленности района в 1990 – 1998 гг.:
Из графика 3.1 видно, что для изучаемого периода времени (1990 – 1998 гг.) уравнение прямой достаточно полно отображает общую тенденцию развития явления. Для выравнивания ряда динамики по прямой используют уравнение: yt=a0+a1t. Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров а0 и а1:
где у – исходные (эмпирические) уровни ряда динамики; n – число членов ряда; t – время. Решение системы уравнений позволяет получить выражения для параметров а0 и а1:
В рядах динамики техника расчета параметров уравнения упрощается. Для этой цели показателям времени t придают такие значения, чтобы их сумма была равна нулю, т.е. Применительно к данному примеру, в котором число исходных (эмпирических) уровней ряда – нечетное (n=9), это выполнимо при следующих обозначениях:
При условии, что
откуда
Произведем расчет необходимых значений в таблице 3.4.
Таблица 3.4
По итоговым данным определим параметры уравнения:
Значение Для случая нечетного числа уровней ряда динамики используется формула:
В результате получаем следующее уравнение общей тенденции ряда динамики: Уt=307+21,92t. Заметим, что при упрощенном способе расчета ( 1990 г. уt=307 +21,92(-4)»219,32; 1991 г. yt=307+21,92(-3)»241,24 и т.д. (значения уt в таблице 5.2) Для проверки расчета значений уt используется формула:
В нашем примере Полученные величины теоретических уровней ряда уi нанесем пунктирной линией на график с эмпирическими данными (рисунок 3.1). Эта линия и есть графический образ общей тенденции выпуска продукции предприятиями легкой промышленности района в 1990 – 1998 гг. При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные или квартальные уровни ряда динамики за несколько лет. Сезонные колебания характеризуются специальными показателями – индексами сезонности Is. Способы определения индексов сезонности различны; они зависят прежде всего от характера общей тенденции ряда динамики. Для ряда внутригодовой динамики, в которой не наблюдается общая тенденция роста (или она незначительна), изучение сезонности основано на методе постоянной средней. Определение средних индексов сезонности в таких рядах производится по формуле:
где
Пример 7. Имеются данные о распределении браков, заключенных населением города, по месяцам 1996 – 1998 гг. (таблица 3.5).
Таблица 3.5
Для выявления характера общей тенденции данного ряда внутригодовой динамики произведем укрупнение месячных периодов в годовые уровни и определим темпы роста (таблица 3.6).
Таблица 3.6
Весь ход расчета индексов сезонности методом постоянной средней изложим в таблице 3.7.
Таблица 3.7
Совокупность исчисленных для каждого месяца годового цикла индексов сезонности характеризует сезонную волну развития изучения явления во внутригодовой динамике. Для получения наглядного представления о сезонной волне изобразим полученные индексы сезонности в виде линейного графика (рисунок 3.2).
I II III IV V VI VII VIII IX X XI XII
Рисунок 3.2 – Сезонная волна заключения браков населением города в 1996 – 1998 гг. по месяцам
Если в ряду внутригодовой динамики имеется ярко выраженная общая тенденция роста, то индексы сезонности определяются на основе методов, позволяющих исключить (элиминировать) влияние тенденции роста. Рассмотрим применение одного из таких приемов на решении типовой задачи, в которой индексы сезонности определяются на основе аналитического выравнивания по прямой. В зависимости от качественной особенности изучаемого явления, а также вида исходных данных ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом первоначальными являются ряды динамики абсолютных величин, которые могут быть моментными или интервальными рядами динамики. Отнесение ряда динамики к тому или иному виду имеет важное значение для их изучения. Выбор соответствующих приемов и способов анализа зависит от задач исследования и определяется характером исходных данных. Поэтому, приступив к анализу рядов динамики, важно правильно их классифицировать. При изучении ряда динамики возникает необходимость получения обобщающей величины его абсолютных уровней. Для этого определяют средний уровень ряда как среднюю величину из совокупности абсолютных уровней ряда динамики за те или иные периоды времени. В интервальном ряду динамики расчет среднего уровня ряда производится по методу средней арифметической простой (не взвешенной):
где у – абсолютные уровни ряда; n – число уровней. Методы расчета среднего уровня ряда динамики зависят от вида ряда динамики и способов получения статистических данных.
3.2 Задачи для самостоятельного выполнения
Задача 1. Определите вид рядов динамики, характеризующих изменение следующих статистических показателей: а) численности населения (по состоянию на начало каждого года); б) численности фермерских хозяйств (по состоянию на начало каждого года); в) вкладов населения в учреждения Сбербанка (на конец каждого года); г) числа родившихся по годам; д) денежных доходов населения по годам; е) индекса потребительских цен на товары и услуги населению (по месяцам за ряд лет); ж) распределения розничного товарооборота по всем каналам реализации по формам собственности по годам; з) среднемесячной заработной платы работников по отраслям экономики по годам; и) удельного веса новой товарной продукции машиностроения в общем объеме продукции по годам. Задача 2. Имеются следующие данные о розничном товарообороте района:
Таблица 3.8 Динамика розничного товарооборота района за 2004-2009 г.г. В млн. рублей
Приведите ряды динамики к сопоставимому виду (сомкните ряды). Укажите вид полученного ряда динамики. Постройте линейную диаграмму. Задача 3. Имеются данные о производстве товаров культурно бытового назначения в среднем за сутки (таблица 3.9).
Таблица 3.9 Динамика суточного производства товаров культурно-бытового назначения за 2008 -20011 г.г. В тыс. штук
Приведите ряды динамики к одному основанию. Исчислите коэффициенты опережения производства холодильников к производству радиоприёмников и телевизоров, а так же производства телевизоров к радиоприёмникам. Сделайте краткие выводы. Задача 4. Имеются следующие данные о товарных запасах магазина розничной торговли за первый квартал 2011 г. (таблица 3.10).
Таблица 3.10 Динамика товарных запасов магазина в первом квартале 2011 г. В тыс. рублей
Определить средние товарные запасы магазина за первый квартал: а) продовольственных товаров; б) непродовольственных товаров; в) продовольственных и не продовольственных товаров вместе. Задача 5. Объем производства часов предприятиями региона на начало каждого месяца первого полугодия 2011 года характеризуется следующими данными (таблица 3.11).
Таблица 3.11 Динамика объема производства часов за первое полугодие 2011 г.
Известно, что объем производства часов за 3 квартал составил 21,7 млн. шт., а за 4 квартал – 21,8 млн. шт. Определить средний объем производства часов предприятиями региона за первое полугодие, за второе полугодие и за 2011 год в целом. Задача 6. Списочная численность работников предприятия составляла: с 1 по 10 сентября – 100 чел.; с 11 по 15 сентября – 120 чел.; с 16 по 26 сентября – 140 чел.; с 27 по 30 сентября – 130 чел. Определить среднесписочную численность работников за сентябрь. Задача 7. Имеются следующие данные о производстве продукции промышленным предприятием за 2006-2011 г.г. (таблица 3.12).
Таблица 3.12 Динамика производства продукции предприятия в сопоставимых ценах за 2006–2011 г.г. В млн. рублей
Для анализа динамики производства продукции предприятия необходимо определить: 1) среднегодовое производство за 2006-2011 г.г.;2) ежегодные (цепные) и базисные абсолютные приросты, темпы роста и темпы прироста; 3) абсолютное значение одного процента прироста; 4) среднегодовой абсолютный прирост; 5) среднегодовой темп роста и среднегодовой темп прироста; 6) среднее значение одного процента прироста. Полученные данные представить в таблице и проанализировать их. Изобразить динамику производства продукции на графике. Задача 8. Имеются следующие данные о розничном товарообороте региона за 2008-2010 г.г. (таблица 3.13).
Таблица 3.13 Динамика розничного товарооборота региона за 2008-2010 г.г.
Для изучения общей тенденции розничного товарооборота региона по месяцам за 2008-2010 г.г. проведите: 1) преобразование исходных данных путем укрупнения периодов времени: а) в квартальные уровни; б) в годовые уровни; 2) сглаживание квартальных уровней розничного товарооборота с помощью скользящей средней. Изобразите графически фактические и сглаженные уровни ряда динамики. Сформулируйте выводы. Задача 9. Используя данные задачи 8: 1) произведите аналитическое выравнивание и постройте модель общей тенденции производства продукции предприятия за 2006-2011 г.г.; 2) определите выравненные (теоретические) уровни ряда динамики и нанесите их на график с фактическими данными. Сформулируйте выводы. Задача 10. Имеются следующие данные о реализации картофеля на продовольственных рынках города за три года:
Таблица 3.14 Динамика реализации картофеля на продовольственных рынках города В тыс. рублей
Измерьте сезонные колебания реализации картофеля, исчислив индексы сезонности методом отношений средних месячных и постоянной средней. Постройте график сезонной волны продажи картофеля. Объясните, для чего измеряют сезонные колебания. 3.3 Контрольные вопросы 1. Дайте определение ряда динамики. Из каких элементов он состоит? 2. Какие динамические ряды называются моментными и интервальными? 3. Назовите важнейшее условие правильного построения динамического ряда. 4. Какие приемы применяются для преобразования несопоставимых рядов динамики в сопоставимые? 5. Какие статические показатели анализа ряда динамики Вы знаете? Как они исчисляются? 6. Какая существует взаимосвязь между последовательными цепными коэффициентами роста и базисным коэффициенто
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.122.2 (0.016 с.) |

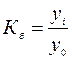 .
.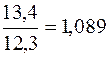 ;
;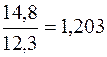 ;
;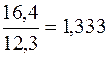 ;
;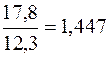 ;
;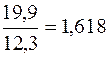 .
.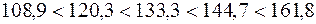
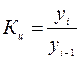 .
. ;
;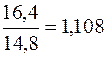 ;
;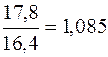 ;
;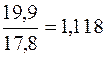 .
.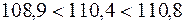 .
.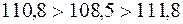 .
.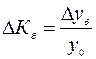 .
.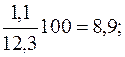
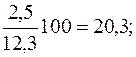
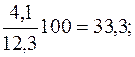
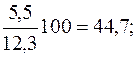
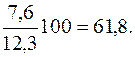
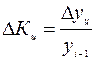 .
.
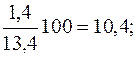



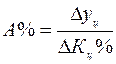 .
.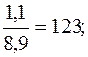
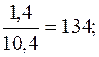
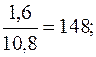
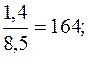

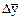 . Способы расчета среднего абсолютного прироста зависят от характера исходных данных.
. Способы расчета среднего абсолютного прироста зависят от характера исходных данных. .
.
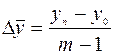 ,
,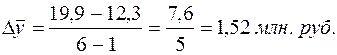
 .
.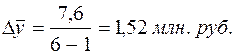 .
.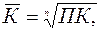
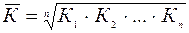 ,
,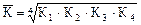 приведенные выше данные, получаем:
приведенные выше данные, получаем: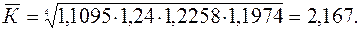
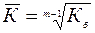 ,
,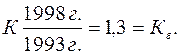
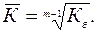
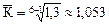 , или 105,3%.
, или 105,3%. , или 104,%.
, или 104,%.




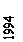


 исходные (эмпирические) данные,
исходные (эмпирические) данные, выравненные (теоретические) данные
выравненные (теоретические) данные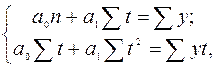
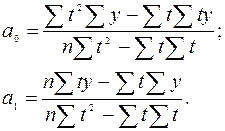
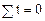 .
. , исходные нормальные уравнения принимают вид:
, исходные нормальные уравнения принимают вид: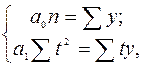
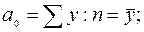

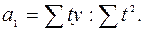

 можно вычислить и другим путем.
можно вычислить и другим путем.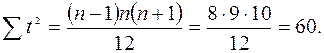
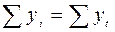
 ; следовательно, значения уt определены верно.
; следовательно, значения уt определены верно.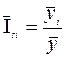 ,
,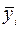 – осредненные эмпирические уровни ряда по одноименным периодам;
– осредненные эмпирические уровни ряда по одноименным периодам; - общий средний уровень ряда.
- общий средний уровень ряда.
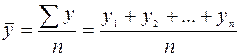 ,
,


