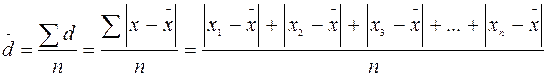Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль II. Аналитическая статистикаСодержание книги Поиск на нашем сайте
ТЕМА 2. МЕТОД АБСОЛЮТНЫХ, ОТНОСИТЕЛЬНЫХ И СРЕДНИХ ВЕЛИЧИН. ЭКОНОМИЧЕСКИЕ ИНДЕКСЫ
2.1 Методические указания и примеры решения задач
Абсолютные статистические величины, характеризуя численность единиц изучаемой совокупности или объемы присущих им признаков, всегда являются числами именованными. В зависимости от качественной особенности изучаемого явления и задач исследования эти величины выражаются в различных единицах измерения: натуральных, трудовых и денежных. При учете продукции и товаров в натуральном выражении часто применяются условные единицы измерения. Сущность применения условных единиц измерения состоит в том, что отдельные разновидности изучаемой совокупности выражаются в единицах одного признака, условно принятого за единицу измерения. Поэтому основной вопрос применения условных единиц измерения состоит в выборе признака, по которому устанавливаются соответствующие коэффициенты пересчета. Пример 1. В отчетном периоде поставка молочной продукции в торговую сеть города характеризуется следующими данными:
Требуется определить общий объем поставки молочной продукции торговой сети города в отчетном периоде. При определении общего объема поставки отдельные виды молочной продукции выражаются в единицах цельномолочной продукции. К цельномолочной продукции относятся молоко, сливки, сметана, ацидофилин, кефир, простокваша, сырковая масса, творог, сырки и другие продукты из цельного молока. Цельномолочная продукция исчисляется в единицах массы путем пересчета каждого вида молочной продукции на молоко по установленным коэффициентам:
Исходя из данных коэффициентов, пересчет поставки отдельных видов молочной продукции в единицах массы молока представим в таблице 2.1.
Таблица 2.1
Таким образом, общий объем поставок цельномолочной продукции в торговую сеть города составил в отчетном периоде 1674,6 т. Относительные статистические показатели. Относительные величины выполнения плана дают количественную характеристику выполнения плановых заданий. Их широкое применение в экономическом анализе обусловлено практикой планового управления народным хозяйством. Способы вычисления относительных величин выполнения плана зависят от характера показателей, выражающих плановое задание. Так, для экономических явлений, которым свойственно поступательное развитие во времени, плановыми заданиями обычно устанавливается достижение в предстоящих периодах тех или иных абсолютных (или средних) уровней. Относительные величины выполнения плана определяются для них как процентное отношение фактически достигнутой в отчетном периоде абсолютной величины уровня к абсолютной величине уровня планового задания:
Пример 2. Имеются следующие данные о производстве в отчетном периоде продукции промышленными предприятиями города:
Таблица 2.2
В последней графе определены относительные величины выполнения плана выпуска продукции в отчетном периоде по отраслям производства и по промышленности города в целом. Для наглядного представления итогов выполнения промышленностью города плана производства продукции полученные данные целесообразно нанести на полосовой график (рисунок 2.1).
1 – машиностроение и металлообработка; 2 – текстильная промышленность; 3 – пищевая промышленность; 4 – вся промышленность
Рисунок 2.1 – Выполнение плана производства продукции промышленности предприятиями города (в процентах)
Для некоторых явлений задания плана предусматривают не рост, а снижение уровней на ту или иную величину. Относительные величины выполнения плана в таких случаях определяются путем сравнения фактически достигнутого и запланированного снижения уровня:
Пример 3. Планом на 1998 г. намечено снижение себестоимости изделия А на 1,5 руб. при уровне себестоимости этого изделия 75,0 руб. Фактически в 1998 г. себестоимость этого изделия составила 73,44 руб. Определите относительную величину выполнения плана по снижению себестоимости изделия А в 1998 г. Для вычисления процента выполнения плана по снижению в 1998 г. себестоимости изделия А найдем фактическую величину снижения себестоимости: 75,0 – 73,44 = 1,56 (руб.). Рассчитаем относительную величину выполнения плана как отношение величины фактического снижения себестоимости (1,56) к величине снижения себестоимости по плановому заданию:
Таким образом, плановое задание по снижению себестоимости изделия А в 1998 г. перевыполнено на 4,0%. В экономическом анализе плановое задание может быть выражено и в форме относительной величины, т.е. в виде коэффициента роста или прироста уровня в планируемом периоде по сравнению с уровнем базисного периода. В этом случае относительная величина выполнения плана определяется из процентного сопоставления коэффициента фактического роста явления с плановым коэффициентом:
Пример 4. Прирост выпуска продукции отрасли по плану на 1998 г. должен составить 7,5%. Фактический рост выпуска продукции в этом году составил 109,5%. Определите относительную величину выполнения плана отраслью по выпуску продукции.
Заданный планом прирост выпуска продукции (7,5%) выражаем в форме коэффициента роста выпуска продукции в 1998г. по сравнению с 1997 г.: 1+ 0,075 = 1,075. Фактический процент роста выпуска продукции (109,5%) выражаем в форме коэффициента:
С помощью полученных коэффициентов рассчитываем относительную величину выполнения плана:
т.е. в 1998 г. план выпуска продукции перевыполнен отраслью на 1,9%. Относительные величины структуры характеризуют долю (удельный вес) составных частей целого в их общем итоге и обычно выражаются в виде коэффициентов (доли единиц) или в процентах. Важное значение относительных величин структуры в экономической статистике заключается в том, что они применяются для изучения состава (строения) статистической совокупности. Сопоставление структуры явлений, сосуществующих в пространстве, позволяет выявить особенности их внутреннего строения. Сравнение же структуры явления, развивающегося во времени, позволяет изучать происходящие в явлении структурные сдвиги (изменения). При определении относительных величин структуры сравниваемыми величинами могут быть или численности отдельных групп статистической совокупности, или объемы их признаков. За основание (базу) сравнения принимается общий итог статистической совокупности. Относительные величины динамики характеризуют развитие изучаемого явления во времени. Они позволяют при анализе данных, характеризующих развитие явления во времени, выявлять направление развития и измерять темпы роста. Относительные величины динамики (темпы роста) исчисляются как отношения абсолютных (или средних) уровней ряда и выражаются в форме коэффициентов или процентов. Пример 5. Потребление кожаной обуви в стране характеризуется следующими данными (на душу населения; пар в год):
Для анализа потребления обуви требуется определить относительные величины динамики. Для выявления направления и характера изменений потребления обуви за 1950–1995 годы по сравнению с дореволюционным 1913 г. определим базисные темпы роста (Кб):
где yi – уровень изучаемого периода; y0 – базисный уровень.
Последовательно сравним уровни 1950, 1960, 1970, 1980 и 1995 гг. yi с уровнем 1913 г. y0:
1950 1960 1970 Из полученных базисных относительных величин динамики (темпов роста) видно, что за указанные годы потребление обуви неуклонно возрастало: 2,75 < 4,75 < 6,0 < 7,5 < 8,0.
В 1995 г. потребление обуви на душу населения было в 8 раз больше, чем в дореволюционном 1913 г. Для выявления характера изменений потребления обуви по отдельным периодам (этапам) экономического развития произведем расчет цепных темпов роста Кц:
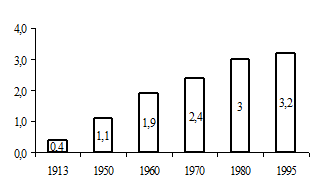
где yi – уровень изучаемого периода; yi-1 – уровень предшествующего периода. Определим цепные темпы роста: 1950 1960 1970 Из полученных цепных относительных величин динамики (темпов роста) видно, что по отдельным этапам экономического развития также происходило увеличение потребления обуви населением. Представим исходные уровни ряда динамики в виде столбиковой диаграммы (рисунок 2.2).
Рисунок 2.2 – Потребление обуви (кожаной) на душу населения в России в 1913–1995 гг. (в год пар)
Данная форма графического изображения уровней ряда динамики удобна тем, что расстояние столбиков (прямоугольников) друг от друга не зависит от величины интервалов времени. Представим графически полученные в расчетах базисные относительные величины динамики. Для этой цели чаще всего используется линейная диаграмма (рисунок 2.3).
Рисунок 2.3 – Темпы роста потребления обуви (кожаной) в 1913 – 1995 гг. в год на душу населения (в процентах к 1913 г.)
В системе координат нанесем на ось ординат базисные темпы роста (в процентах), а на ось абсцисс – показания времени. Из данного графика видно, что положение кривой определяется не только значениями базисных темпов роста, но и интервалами времени между датами. Важное значение при анализе экономических явлений имеют относительные величины координации. В отличие от относительных величин структуры, выражающих удельные веса частей в целом, относительные величины координации характеризуют соотношение частей изучаемой статистической совокупности, которое показывает, во сколько раз сравниваемая часть явления больше или меньше части, принимаемой за основание (базу) сравнения. Относительные величины координации выражаются в кратных отношениях. Пример 6. За истекший год получены следующие данные о численности детей, родившихся в области, чел.: мальчики – 40 357; девочки – 38 019. Для определения относительной величины соотношения численности мальчиков и девочек сопоставим между собой исходные данные (приняв за базу сравнения численность родившихся девочек):
т.е. на каждые 100 девочек рождались 106 мальчиков. В статистике часто приходится сопоставлять значения одноименных признаков по нескольким совокупностям. В результате получают относительные величины сравнения. Относительные величины интенсивности характеризуют степень насыщенности изучаемым явлением определенной среды. Они выражают соотношение разноименных, но связанных между собой величин и исчисляются как отношение величины изучаемого явления к объему той среды, в которой происходит развитие явления. Относительные величины интенсивности являются именованными числами и могут выражаться в кратких отношениях, процентах, промилле и других формах. Пример 7. Имеются следующие данные по району: число родившихся за год детей составляет 1701 человек; среднегодовая численность населения 94 980 человек. Определите относительную величину интенсивности, характеризующую рождаемость детей. Для решения задачи определим коэффициент рождаемости детей:
или 18% (промилле). Таким образом, рождаемость детей в районе в расчете на 100 человек населения составляла 18 человек. Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Необходимо учесть, что средняя величина должна вычисляться с учетом экономического содержания определяемого показателя. Каждый показатель имеет свое, только ему присущее содержание. Например,
Такой подход позволяет правильно определить среднюю величину признака, выбрать форму средней. Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений. Отдельные значения признака называют вариантами и обозначают через x (x1, x2, x3, …, xn), число единиц в совокупности обозначают через n, среднее значение признака – через х. Следовательно, средняя арифметическая простая равна:
Пример 8. Имеются данные о производстве рабочими продукции «А» за смену:
Таблица 2.3
В данном примере варьирующий признак – выпуск продукции за смену. Численные значения признака (16, 17 и т. д.) называют вариантами. Определим среднюю выработку продукции рабочими данной группы:
Простая средняя арифметическая применяется в случаях, когда имеются значения признака, т. е. данные не сгруппированы. Если данные представлены в виде рядов распределения или группировок, то средняя исчисляется иначе.
Пример 9. Имеются следующие данные о заработной плате рабочих-сдельщиков.
Таблица 2.4
По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются несколько раз. Так, варианта X1 встречается в совокупности 2 раза, а варианта X3 – 16 раз и т.д. Число одинаковых значений признака в рядах распределения называется частотой, или весом и обозначается символом f. Исчислим среднюю заработную плату одного рабочего
Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих произведений дает общий фонд заработной платы всех рабочих. В соответствии с этим расчеты можно представить в общем виде:
Полученная формула называется средней арифметической взвешенной. Из нее видно, что средняя зависит не только от значений признака, но и от их частот, т. е. от состава совокупности, от ее структуры. Изменим в условии задачи состав рабочих и исчислим среднюю в измененной структуре. Пример 10. Представим данные о численности рабочих в условии приведенной выше типовой задачи в относительных величинах:
Таблица 2.5
Средняя заработная плата рабочего, взвешенная по процентным соотношениям, будет равна средней, полученной при решении типовой задачи 3:
Если весами являются частоты, выраженные в коэффициентах, то вычисления упрощаются. Так как сумма коэффициентов всегда равна единице, то расчет средней сводится к определению суммы произведений вариант на частоты (в данном случае коэффициенты):
Расчеты средней арифметической могут быть громоздкими, если варианты и веса имеют большее значение. Однако использование следующих основных математических свойств средней арифметической взвешенной позволяет значительно упростить вычисления. Приведем основные свойства средней арифметической: 1. Если уменьшить все варианты на какое-либо произвольное постоянное число (A), то новая средняя уменьшится на то же число. 2. Если уменьшить все варианты в одинаковое число раз (K), то средняя уменьшится во столько же раз. 3. Если уменьшить или увеличить веса (частоты) всех вариант на какое-либо постоянное число (A), то средняя арифметическая не изменится. 4. Сумма отклонений всех вариант от общей средней равны нулю. Рассмотрим методику расчета средней с использованием этих свойств. Пример 11. Имеются следующие данные о времени горения электроламп:
Таблица 2.6
Для сравнения рассчитаем среднее время горения электроламп обычным, уже известным нам способом, по средней арифметической взвешенной. Результаты расчетов представлены в таблице 3.3. Таким образом, среднее время горения электроламп будет равно:
Пример 12. Используя данные типовой задачи 4 о времени горения электроламп, произведем расчет арифметической взвешенной по способу моментов. Рассмотрим методику расчета, результаты которого приведены в таблице 2.7. Воспользуемся первым свойством средней взвешенной, которое позволяет исчислить среднюю, не по фактическим значениям вариант, а по отклонениям вариант от постоянной А. В качестве постоянной А принято брать какую-либо серединную варианту ряда с наибольшей частотой. В нашем примере это x=A=1300. Найдем отклонения вариант от этой величины и получим значения новых вариант: x–A=x–1300.
Таблица 2.7
Воспользуемся далее вторым свойством и уменьшим варианты в несколько раз. В качестве кратного числа возьмем величину интервала ряда распределения, которая равна 200. Разделив значения вариант (x–A) на 200, получим новые значения вариант:
Используя свойство третье, сократим частоты в 10 раз и произведем умножение полученных значений на варианты:
Для получения средней арифметической взвешенной необходимо разделить алгебраическую сумму взвешенных вариант на сумму весов:
Для вычисления средней необходимо произвести корректировку полученного результата с учетом свойств. Для этой цели нужно полученное значение умножить на величину интервала и прибавить к постоянной величине:
В результате расчетов по данной формуле получим среднюю:
Наряду со средней арифметической в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной.
Пример 13. Бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затрачивал на одну деталь 12 мин, второй – 15 мин, третий – 14 мин, четвертый – 16 мин, пятый – 14 мин. Определите среднее время, необходимое на изготовление одной детали. На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:
Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим образом:
Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали равно:
Это же решение можно представить иначе:
Таким образом, формула для расчета средней гармонической простой будет иметь вид:
Пример 14. Издержки производства и себестоимость единицы продукта А по трем заводам характеризуются следующими данными:
Таблица 2.8
Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателей и исходные данные.
Таким образом, формулу для расчета средней гармонической взвешенной можно представить в общем виде:
Характеристиками вариационных рядов наряду со средними являются мода и медиана. Мода - есть величина признака (варианты), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианты с наибольшей частотой.
Пример 15. Распределение проданной обуви по размерам характеризуется следующими показателями:
Таблица 2.9
В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей. Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
где XMo- начальное значение интервала, содержащего моду; iMo- величина модального интервала; fMo- частота модального интервала; fMo-1- частота интервала, предшествующего модальному; fMo+1- частота интервала, следующего за модальным. Пример 16. Рассмотрим пример расчета моды. Распределение предприятий по численности промышленно-производственного персонала характеризуется следующими данными (таблица 2.10).
Таблица 2.10
В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения. Введем следующие обозначения: XMo=400; iMo=100; fMo=30; fMo-1=7; fMo+1=19. Подставим эти значения в формулу моды и произведем вычисления:
Медианой в статистике называется варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет начальное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд – это расположение единиц совокупности в возрастающем или убывающем порядке). Например, стаж пяти рабочих составил 2, 4, 7, 8 и10 лет. В таком упорядоченном ряду медиана – 7 лет. По обе стороны от нее находится одинаковое число рабочих. Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Пусть теперь будет не пять человек в бригаде, а шесть, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В этом ряду имеются две варианты, сходящие в центр ряда. Это варианты 6 и 7. Средняя арифметическая из этих значений и будет медианой ряда:
Рассмотрим пример расчета медианы в дискретном ряду. Пример 17. Используя данные условия типовой задачи 9 настоящей главы, определим медиану заработной платы рабочих.
Таблица 2.11
Для определения медианы надо подсчитать сумму накопленных частот ряда (гр. 3 табл. 2.11). Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину. В нашем примере сумма частот составляет 40, ее половина – 20. Накопленная сумма частот ряда получилась равна 24. Варианта, соответствующая этой сумме, т. е. 150 руб., и есть медиана ряда. Если же сумма накопленных частот против одной из вариант равна точно половине суммы частот, то медиана определяется как средняя арифметическая этой варианты и последующей. Медиана будет равна:
Рассмотрим расчет медианы в интервальном вариационном ряду. Медиана интервального вариационного ряда распределения вычисляется по формуле:
где XMe – начальное значение интервала, содержащего медиану; iMe – величина медианного интервала;
SMe-1 – сумма накопленных частот, предшествующих медианному интервалу; fMe – частота медианного интервала. Пример 18. Используя данные типовой задачи 16, рассчитаем медиану в интервальном вариационном ряду.
Таблица 2.12
Определим прежде всего медианный интервал. В данной задаче сумма накопленных частот, превышающая половину всех значений (41), соответствует интервалу от 400 до 500. Это и есть медианный интервал, в котором находится медиана. Определим ее значение по приведенной выше формуле. Известно, что: XMe=400; iMe=100;
SMe-1=11; fMe=30. Следовательно,
Показатели вариации. Для характеристики совокупностей и исчисленных средних величин важно знать, какая вариация изучаемого признака скрывается за средними. Вариация – различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. В статистической практике для изучения и измерения вариации используют различные показатели (меры) вариации в зависимости от поставленных задач: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отношение, коэффициент вариации. Рассмотрим пример расчета размаха вариации. Пример 19. Имеются следующие данные о производительности труда рабочих в двух бригадах:
Таблица 2.13
Средняя производительность труда в обеих бригадах одинакова:
Однако в первой бригаде вариация производительности труда значительно больше, чем во второй, и можно сказать, что первая бригада по своему составу в отношении изучаемого признака менее однородна, чем вторая. Для измерения степени варьирования признака служат показатели вариации. Наиболее простым показателем вариации является размах вариации R, который определяется как разность между наибольшим и наименьшим значением признака: R=xmax – xmin. Для нашего примера размах вариации производительности труда для первой бригады составляет: 18 – 2 = 16; для второй бригады: 12 – 8 = 4. Этот показатель прост в вычислении и указывает на общие размеры вариации, но он не дает представления о степени колеблемости внутри совокупности, так как вычисляется на основе только двух крайних значений признака совокупности. Чтобы определить вариацию признака единиц совокупности, надо исчислить отклонения каждого значения признака х от средней арифметической
При этом отклонения могут быть положительными или отрицательными в зависимости от значений признака. Из полученных значений отклонений необходимо исчислить среднюю арифметическую:
Известно, что сумма отклонений всех значений признака от средней арифметической будет равна нулю. Для определения среднего линейного отклонения, которое часто называют средним абсолютным отклонением, необходимо взять значения отклонений по абсолютной величине без учета знака. Итак, среднее линейное (абсолютное) отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Пример 20. Исчислим среднее линейное отклонение по данным типовой задачи 19.
Таблица 2.14
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 2571; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.244 (0.01 с.) |




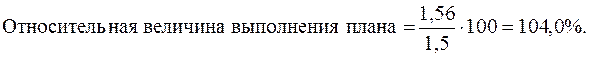
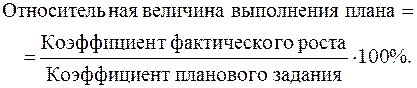
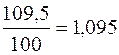 .
.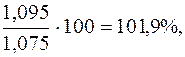
 ,
,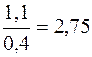 1980
1980 
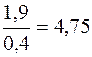 1995
1995 

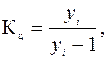
 1980
1980 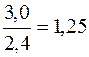
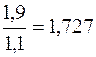 1995
1995 
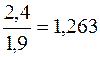


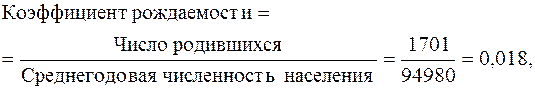
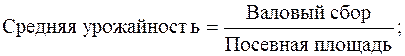
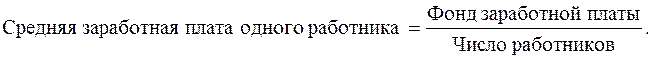

 .
.
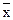 :
: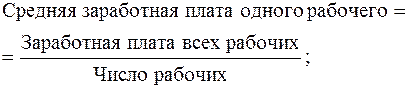
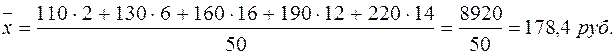
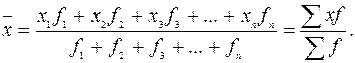
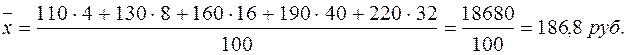
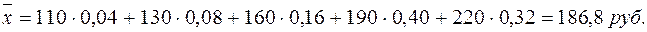
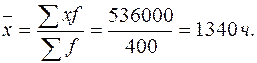
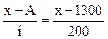

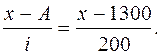
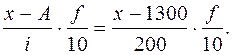
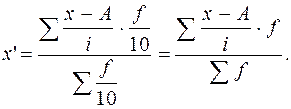
 , или в развернутом виде:
, или в развернутом виде:

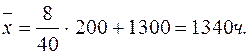

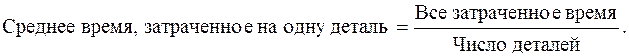
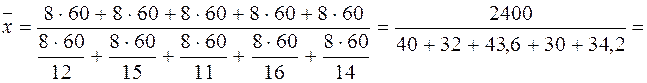
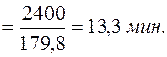
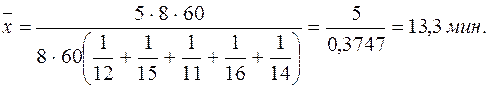
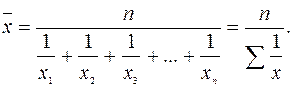

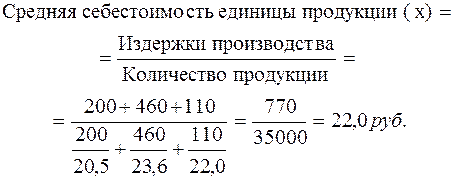
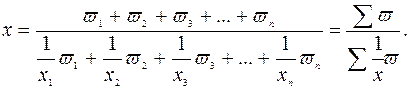

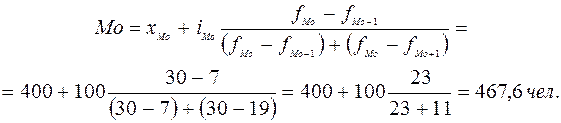

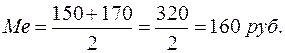 .
.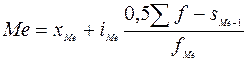 ,
,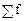 - сумма частот ряда;
- сумма частот ряда;
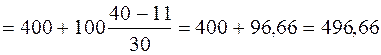
 .
.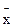 :
: и т. д.
и т. д.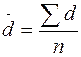 .
.