
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наглядное представление результатов корреляционного исследованияСодержание книги
Похожие статьи вашей тематики
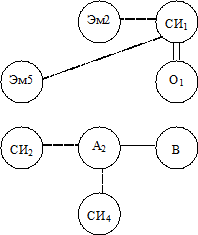
Поиск на нашем сайте Результаты корреляционного исследования наглядно удобно представлять в виде корреляционного графа или корреляционных плеяд. Корреляционный граф – это фигура из вершин и линий их соединяющих. Вершинами являются исследуемые признаки или качества. Они могут обозначаться полными названиями, сокращениями, цифрами. Тип линий между двумя вершинами выражает знак и уровень статистической значимости коэффициента корреляции, который рассчитан для данных двух признаков. Когда граф имеет много вершин, изобразить его на одном рисунке трудно, получается множество запутанных линий, которые сложно визуально воспринимать. В этом случае граф изображают по частям, называемыми плеядами. Плеяды могут выделяться по двум принципам: 1) по уровню значимости связи; 2) относительно каждой вершины. Правила кодирования - в корреляционном графе рассматриваются и кодируются лишь коэффициенты корреляции, достоверно отличающиеся от нуля, то есть превышающие или равные граничные значения коэффициента корреляции хотя бы на 5% уровне значимости; - коэффициенты корреляции, не превышающие однопроцентного порога достоверности, то есть 0,01<рэмп≤0,05, кодируются одной линией, тогда как при рэмп≤0,01 – двумя линиями. - положительные связи кодируются сплошной линией, отрицательные – пунктирной.
Интерпретация результатов корреляционного анализа заключается в объяснении полученных связей на основе теоретического анализа и здравого смысла.
Пример решения задачи Критерий rs- Спирмена Достоверна ли связь между агрессивностью и инициативностью?
Гипотезы: Н0: Связь между агрессивностью и инициативностью не достоверна Н1: Связь между агрессивностью и инициативностью достоверна
Коэффициент корреляции вычисляется по формуле:
где Rai – ранговое значение переменной А для i -го участника; Rbi – ранговое значение переменной B для i -го участника; n – объем выборки; Та – поправка на одинаковые ранги в ранговом ряду А; Тb - поправка на одинаковые ранги в ранговом ряду B;
Осуществим ранжирование переменной «агрессивность» и запишем ранг рядом с индивидуальным значением. Затем осуществим ранжирование переменной «инициативность», ранг запишем рядом с соответствующим индивидуальным значением. Результаты вычисления для удобства представим в виде таблицы.
Поправки на одинаковые ранги вычисляются по формуле:
a –объем каждой группы одинаковых рангов в ранговом ряду А b - объем каждой группы одинаковых рангов в ранговом ряду В
В ранговом ряду «А » имеется три группы одинаковых рангов. Объем первой группы одинаковых рангов равен трем, так как ранг «4» встречается три раза. Это можно записать: а 1(4)=3; Объем второй группы одинаковых рангов равен двум: а 2(6,5)=2; Объем третьей группы одинаковых рангов равен двум: а 3(11,5)=2; Таким образом, поправка на одинаковые ранги по переменной А:
В ранговом ряду «В » четыре группы одинаковых рангов. Объем первой группы: b 1(1,5)=2; Объем вторая группы: b 2(3,5)=2; Объем третьей группы: b 3(7)=5; Объем четвертой группы: b4(12)=3 Поправка на одинаковые ранги по переменной B:
Коэффициент корреляции:
Вычисленное значение коэффициента корреляции rs=-0,41. Критические значения при n=14: rs(0,05)=0,54; rs(0,01)=0,68 Силу связи определяет абсолютное значение коэффициента корреляции, то есть знак не учитывается. Поэтому, на оси значимости мы откладываем абсолютное значение коэффициента корреляции. Представим результаты вычисления наглядно.
Статистический вывод: рэмп>0,05, поэтому принимается нулевая гипотеза. Психологический вывод: связь между агрессивностью и инициативностью не достоверна. Задания для самостоятельной работы № 9.1. Установите, являются ли статистически достоверными следующие показатели корреляции переменных: А) коэффициент Пирсона rxy=0,445 для данных двух тестирований в группе, состоящей из 20 испытуемых; Б) коэффициент Пирсона rxy=-0,810 при числе степеней свободы, равном 4; В) коэффициент Спирмена rs=0,415 для группы из 26 человек № 9.2. У 12 школьников шестого класса с помощью Шкалы интеллекта Стенфорда-Бине определен IQ. Успеваемость по химии оценивалась с помощью теста состоящего из 35 вопросов. Определить связаны ли успеваемость по химии и коэффициент интеллекта (IQ). Построить диаграмму рассеивания.
№ 9.3. В таблице представлены результаты арифметического теста и теста чтения. Достоверна ли связь между этими двумя переменными?
№ 9.4. Достоверна ли связь между переменными «Х» и «У»?
№ 9.5. В исследовании, посвященном проблемам ценностной ориентаций, выявлялись иерархии терминальных ценностей по методике М.Рокича. Ранги терминальных ценностей, полученные при обследовании, представлены в таблице. Определить различаются ли ценностные ориентации студента А и студента В.
Ранги терминальных ценностей по списку М.Рокича в индивидуальных иерархиях студента А и студента В
№ 9.6. Изучались ценностные ориентации студентов первокурсников. В исследовании приняло участие 60 студентов факультета психологии, из них 5 юношей и 55 девушек. Для изучения ценностных ориентаций использовали методику Ш.Шварца. Насколько индивидуальный профиль студента коррелирует с усредненным профилем. Значения для типов ценностных ориентаций
№ 9.7. Определить величину коэффициента корреляции r для следующих данных (Гласс, Стенли). Достоверна ли связь между переменными? Построить диаграмму рассеивания. Является ли связь между Х и У – если она существует – линейной или криволинейной?
№ 9.8. Определить, существует ли связь между временем реакции испытуемых и эффективностью их действий (см. задачу №6.3.) для а) контрольной и б) экспериментальной группы. № 9.9. Наблюдения за 12 студентами второго курса колледжа по переменным «семейное положение» и «исключение из колледжа» приведены в таблице (Гласс, Стенли). Достоверна ли связь между семейным положением и успешностью обучения?
№ 9.10. На случайной выборке студентов заочного отделения факультета психологии были получены данные представленные в таблице. Достоверна ли связь между цветом волос и цветом глаз?
№ 9.11. Используя данные задачи №7.6 о подготовленности учеников к вступительным экзаменам в Вуз, проверить соотношение:
№ 9.12. Связь возраста «Х» с результатами вспомогательного теста «цифра-знак» шкалы интеллекта взрослых Векслера. Вычислить корреляционное отношение, построить диаграмму рассеивания.
№ 9.13.
№ 9.14. Pезультаты тестирования группы из 10 учеников проранжированны в соответствии с их способностями к математике и музыке. Определить, достоверна ли связь между математическими и музыкальными способностями.
№ 9.15. В таблице приводятся исходные оценки 12 учащихся школы по тесту абстрактного и вербального мышления. Достоверна ли связь между абстрактным и конкретным мышлением?
№ 9.16. Исследователь решил установить, связан ли рост человека с его полом. Проверьте гипотезу исследователя по данным, приведенным в таблице
№ 9.17. Исследователь решил установить, существуют ли гендерные различия в показателях интеллекта. Проверьте гипотезу исследователя по данным приведенным в таблице.
№ 9.18. Приведенные данные – характеристики людей и методы их измерения – таковы (Гласс, Стенли).
В каждом из следующих примеров определите один или более коэффициентов корреляции, пригодных для описания связи между двумя переменными: А) Пол и рост; Б) Тревожность и интеллект; В) Пол и тревожность; Г) Пол и рост; Д) Пол и политическая принадлежность; Е) Политическая принадлежность и интеллект.
№ 9.19. Сделайте выводы о статистической достоверности и степени выраженности корреляционных отношений при числе степеней свободы, равном 25, если известно, что Sd2 составляет а) 1200; б) 1555; в) 2300. № 9.20. Для выявления особенностей взаимосвязи между компонентами мотивационно-личностной и операциональной составляющей коммуникативной компетентности было проведено корреляционное исследование. Для вычисления коэффициента корреляции был использован критерий Спирмена. В исследовании участвовали студенты четвертого курса педвуза, объем выборки - 21 студент. В исследовании был выявлен ряд статистически значимых корреляционных связей. Статистически значимые коэффициенты корреляции представлены в таблице. Представить результаты корреляционного исследования наглядно в виде корреляционного графа и в виде корреляционных плеяд. Приняты следующие обозначения: АП- рефлексивно-перцептивные умения; КИ- когнитивно-информационные умения; ОД- организационно-деятельностные умения; АР- аффективно-регулитивные умения; Сотр - сотрудничество Изб - избегание Присп- приспособление НТ - невербальное творчество Пр - прогнозирование Эго - эгоцентризм
РЕГРЕССИОННЫЙ АНАЛИЗ
Регрессионный анализ – область статистического анализа, изучающая зависимость измерений значений переменных от одной или нескольких зависимых переменных (факторов). Задачами регрессионного анализа являются установление формы зависимости между переменными, оценка функции регрессии, оценка неизвестных значений (прогноз значений) зависимой переменной. Регрессионный анализприменим только по отношению к количественно выраженным переменным, измеряемым в метрических шкалах. Точная зависимость Y от X называется уравнением регрессии Y=f(X). Одномерное линейное уравнение регрессии: Y = b1X + b0 Уравнение позволяет предсказывать для любого значения Х соответствующее значение переменной Y. Для каждой пары данных (xi, yi), полученных в ходе эмпирического исследования, вычисленное по уравнению регрессии значение ỹ и значение yi чаще всего не совпадает. Yi=b1Xi + b0 + ei, - для точки с координатами (Xi, Yi) где ei – ошибка оценивания Y для i –го объекта Значения ei=yi-ỹ называются ошибками оценки или остатками. Нахождение коэффициентов регрессии сводится к интегральной минимизации этих остатков таким образом, чтобы их сумма квадратов была минимальной из всех возможных: Параметры линейной регрессии (МНК): Коэффициент регрессии: b1 =
Свободный член регрессии может быть вычислен: Где
Коэффициент регрессии находится в тесной связи с коэффициентом корреляции. Коэффициент корреляции представляет собою среднее геометрическое из коэффициентов регрессии признаков: r= Коэффициент линейной регрессии и коэффициент корреляции Пирсона связаны следующим соотношением:
Где σy, σx – стандартные отклонения этих переменных.
Проверка, насколько данная модель уравнения регрессии действительно удовлетворяет экспериментальным данным осуществляется при помощи F-отношение, по формуле:
где N – объем выборки (число наблюдений). r2xy- коэффициент множественной детерминации Здесь альтернативная гипотеза утверждает, что модель уравнения регрессии действительно удовлетворяет экспериментальным данным. Нулевая гипотеза о том, что между переменными X и Y отсутствует значимая связь. Если, принимается альтернативная гипотеза о регрессионном уравнении в целом, то необходимо проверить частные гипотезы в отношении регрессионных коэффициентов. Стандартная ошибка выборочного коэффициента регрессии может быть рассчитана при помощи следующего уравнения: Sbxy= Достоверность выборочного коэффициента регрессии проверяется с помощью критерия Стьюдента с числом степеней свободы n=n-2 и принятым уровнем статистической значимости. Нулевая гипотеза сводится к предположению, что в генеральной совокупности коэффициент регрессии равен нулю.
Задания для самостоятельной работы № 10.1. Постройте графики для следующих уравнений: а). Y = -2 + 3X b). 2Y = 4 + X.
№ 10.2. Частная школа определила уравнение предсказания для прогноза среднего балла учащихся колледжа, в университете штата по среднему баллу учащихся школы. Уравнение выглядит так: Y = 0,76 + 0,62X. Назовите средний балл в колледже, который получил бы ученик со следующими средними баллами в школе: а) 3,50; б) 1,68; в) 2,10; г) 4,00
№ 10.3. Верно ли, что чем выше величина b1, тем выше коэффициент корреляции Пирсона? № 10.4.
№ 10.5. Проверить исходя из данных задачи № 10.3: 1) b1= rxy 2) Отношение дисперсии предсказанных значений ỹ к дисперсии фактических значений yi равно квадрату коэффициента корреляции между Х и У.
№ 10.6. В экспериментах по изучению слежения с преследованием, выполняемого человеком, измерялось латентное время реакций в зависимости от скорости движения цели. Цель начинала движение мгновенно и двигалась равномерно с некоторой скоростью (Г.В.Суходольский). Результаты представлены в таблице. Предположив, что величина скорости движения цели действует на реакцию испытуемого аналогично тому, как действуют величины стимулов других модальностей, можно думать, что искомая зависимость аналогична закону Пьерона. Следовательно, аппроксимирующая функция должна быть гиперболой. Такое предположение верно, если логарифмы латентного времени реакции в зависимости от логарифмов скорости образуют на графике ряд точек, флуктуирующих около прямой линии.
№ 10.7. В плане комплексного исследования личности у студентов психологического факультета определялся социометрический статус на курсе (Y) и в своей учебной группе (Х). А) Построить уравнения регрессии: У(Х) и Х(У). Б) Проверить достоверна ли связь между статусом студента в группе и его статусом на курсе.
№ 10.8. По первичным данным, представленным в работе А.Д.Резника, построить уравнение регрессии, показывающее зависимость интеллекта детей от интеллекта родителей. Предсказать каким может быть интеллект ребенка, если интеллект родителя: а) IQ=115; б) IQ=100; в) IQ =80; г) IQ=130
Проверить насколько построенное уравнение регрессии соответствует эмпирическим данным. Построить диаграмму рассеивания, с построенной по принципу наименьших квадратов линией предсказания.
ДИСПЕРСИОННЫЙ АНАЛИЗ Исследование влияния переменных факторов на изучаемую переменную по дисперсиям называется дисперсионным анализом. Термин «дисперсионный анализ» происходит от того, что проверка статистических гипотез основана на сравнении выборочных дисперсий с помощью F- критерия Фишера-Снедекора. В англоязычной литературе и программах статистической обработки называется ANOVA/MANOVA. Основная задача дисперсионного анализа – выявление воздействий одной или нескольких независимых переменных (соответственно одно- или многофакторный дисперсионный анализ) на зависимую переменную. Независимую переменную в этом случае принято называть фактором и рассматривать как причину, вызывающую изменение зависимой переменной. Независимая переменная представляет собой качественно определенный (номинативный) признак, имеющий две и более градации. Каждой градации независимой переменной соответствует выборка объектов (испытуемых), для которых определены значения зависимой переменной. Зависимая переменная в экспериментальном исследовании рассматривается как изменяющаяся под влиянием независимых переменных. В модели ANOVA зависимая переменная должна быть представлена в метрической шкале. Нулевая гипотеза формулируется как равенство внутригрупповых средних между собой. Гипотеза о равенстве внутригрупповых средних может быть проверена через анализ вариативностей, так как с увеличением различий между внутригрупповыми средними возрастает факторная дисперсия. Если различий нет, то большую долю в общей дисперсии будет занимать случайная дисперсия. Статистическая проверка гипотезы основывается на применении F – критерия. Метод базируется на предположении о том, что если на объект (группу испытуемых) влияет несколько независимых факторов и их влияние складывается, то общую дисперсию значений признака, характеризующую объект (группу испытуемых), можно разложить на сумму дисперсий, возникающих в результате воздействия каждого отдельного фактора, а также обусловленных случайными явлениями (остаточная дисперсия). Сравнение дисперсий, обусловленных влиянием различных факторов, со случайной (остаточной) дисперсией позволяет оценить значимость вклады каждого из факторов, т.е. оценить достоверность этих влияний.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |


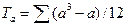 ;
; 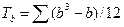
 ;
;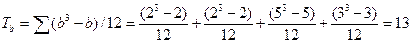
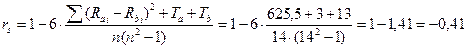


 .
. .
.
 - средние значения переменных X и Y соответственно;
- средние значения переменных X и Y соответственно;

 ,
,
 .
. .
Для наших экспериментальных условий аппроксимирующая гипербола должна быть без свободного члена:
.
Для наших экспериментальных условий аппроксимирующая гипербола должна быть без свободного члена:
 ,
где u – среднее арифметическое значение латентного времени реакции (с);
z – скорость движения (мм/с);
h и a – неизвестные коэффициенты, которые и следует вычислить по данным эксперимента
Определить коэффициенты в уравнении Пьерона по эмпирическим данным.
,
где u – среднее арифметическое значение латентного времени реакции (с);
z – скорость движения (мм/с);
h и a – неизвестные коэффициенты, которые и следует вычислить по данным эксперимента
Определить коэффициенты в уравнении Пьерона по эмпирическим данным.



