
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка достоверности сдвига в значенияхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ИССЛЕДУЕМОГО ПРИЗНАКА Критерии, представленные в данном разделе предназначены для работы с зависимыми выборками. Выборки называются зависимыми (связными), если процедура эксперимента и полученные результаты измерения некоторого свойства, проведенного на одной выборке, оказывают влияние на другую. Примером зависимых выборок является группа, на которой дважды проводилось психологическое обследование (или группа в условиях «до» и «после» воздействия). Типичные сдвиги - сдвиги, которые нам кажутся преобладающими. Нетипичные сдвиги – сдвиги более редкого, противоположного направления.
G – критерий знаков Критерий часто применяется для решения задачи выявления изменения признака. Применяется, если в исследовании два замера (чаще условие «до»-«после»). Составляются ненаправленные гипотезы. Алгоритм. Определить для каждой пары значений направление сдвига d=хпосле-хдо. Подсчитать количество «положительных» (G+) и «отрицательных» (G-) сдвигов. Считать меньшее из двух вычисленных значений нетипичным, Gнетип.. Считать Gэмп= Gнетип. Сопоставить Gэмп с Gкр(n). Где n – общее количество сдвигов. При наличии нулевых сдвигов, общее количество сдвигов (n) меньше объема выборки.
Т – критерий Вилкоксона Критерий применяется для решения задачи выявления изменения признака количественно измеренного. Применяется, если в исследовании два замера (чаще условие «до»-«после»). Данный критерий более мощный, чем критерий знаков, так как учитывает не только направление сдвига, но и его выраженность. Для данного критерия составляются направленные гипотезы. Эмпирическое значение критерия вычисляется по формуле:
где R-ранги, нетипичного направления сдвига
Алгоритм. Определить для каждой пары значений направление и значение сдвига d=xпосле-хдо. Ранжируется ряд, полученный из абсолютных значений сдвигов, т.е. знак сдвига не учитывается. Нулевой сдвиг не ранжируется. Подсчитать суммы рангов: T+ = где R+ – ранговые значения сдвигов с положительным знаком. R- – ранговые значения сдвигов с отрицательным знаком.
Эмпирическое значение критерия (Tэмп) соответствует значению меньшему из двух ранговых сумм. Сопоставить Tэмп с Tкр(n). Где n – общее количество сдвигов. При наличии нулевых сдвигов, общее количество сдвигов (n) меньше объема выборки.
Критерий Критерий можно рассматривать как распространение критерия Вилкоксона на три и большее количество значений признака связной выборки испытуемых. Критерий не позволяет выявить направление изменений, позволяет лишь установить достоверность различий признака в разных условиях. Составляются ненаправленные гипотезы. Эмпирическое значение критерия рассчитывается по формуле:
При этом, где с – количество условий; n – объем выборки; Tj – сумма рангов по j-му условию.
Ранжирование осуществляется по строкам, т.е. ранжируются индивидуальные значения испытуемого, полученные в разных условиях. При общем количестве измерений с=3 и числе испытуемых от 2 до 9 критические значения определяются по таблице Приложения для критерия Фридмана. При общем количестве измерений с=4 и числе испытуемых от 2 до 4 критические значения определяются по таблице Приложения для критерия Фридмана. При большем количестве измерений и/или испытуемых критические значения определяются по таблице для критерия χ2-Пирсона. Число степеней свободы определяется по формуле ν=с-1.
L – критерий Пейджа Критерий применяется для сопоставления показателей измеренных в трех и более условиях на одной и той же выборке испытуемых. Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию. Он не только констатирует различия, но и указывает на направление изменений. Применим когда n≤12 (объем выборки) и количество замеров с≤6. Составляются направленные гипотезы.
Ранжирование осуществляется по строкам, т.е. ранжируются индивидуальные значения участника исследования, полученные в разных условиях (по строке).
Эмпирическое значение критерия рассчитывается по формуле:
Lэмп =
где, Тj – сумма рангов по данному условию. j – порядковый номер, приписанный данному условию в упорядоченной последовательности условий.
Выборки (условия) должны быть упорядочены в соответствии с суммой рангов по выборке. Выборке с меньшей ранговой суммой присваивается значение j=1.
Тест МакНемара (данные представлены в дихотомической шкале)
Значения A и D определяются из таблицы сопряженности
где A – количество человек имеющих: до «+» и «-» после; B – количество человек имеющих: до «+» и «+» после; C - количество человек имеющих: до «-» и «-» после; D - количество человек имеющих: до «-» и «+» после;
По категории «до» - плюс обозначает проявление изучаемого показателя, или его высокое значение; минус – отсутствие проявления изучаемого показателя или его низкое значение. По категории «после» - «плюс» обозначает увеличение изучаемого показателя, «минус» – отсутствие изменения или уменьшение изучаемого показателя. Примеры решения задач Задача. Исследование социального интеллекта студентов специальности информатика проводилось по тесту Гилфорда-Салливена. Достоверно ли изменение социального интеллекта у студентов четвертого курса вследствие проведения тренинга коммуникативной компетентности? В таблице приведены результаты измерения.
Вариант 1. Для решения выбираем критерий знаков.
Гипотезы: Н0: Тренинг коммуникативной компетентности не повлиял на значение социального интеллекта студентов Н1: Тренинг коммуникативной компетентности повлиял на значение социального интеллекта студентов
Для каждой пары значений определить направление сдвига d = хпосле - хдо. Значение записать в таблицу. Подсчитать количество положительных и отрицательных сдвигов. Количество «положительных» сдвигов десять, G+=10; количество «отрицательных» сдвигов три, G-=3. Меньшее из двух значений считается нетипичным сдвигом (Gнетип.), поэтому Gнетип.=3. Считать Gэмп= Gнетип=3. Для принятия решения - выбора гипотезы - необходимо сопоставить Gэмп с Gкр(n), где n – общее количество сдвигов. Общее количество сдвигов n=13, так как положительных сдвигов десять, отрицательных сдвигов три, нулевые сдвиги не учитываются. По таблице определяем критические значения критерия при данном количестве сдвигов. Для уровня статистической значимости р=0,05 критическое значение критерия G0,05=3, для уровня статистической значимости р=0,01 критическое значение критерия G0,01=1. Результаты вычисления представим наглядно.
Статистический вывод: так как рэмп=0,05, нулевая гипотеза Н0 отклоняется и принимается альтернативная гипотеза на уровне статистической значимости р=0,05. Психологический вывод: тренинг коммуникативной компетентности повлиял на социальный интеллект студентов (р=0,05).
Вариант 2. Для решения выбираем T-критерий Вилкоксона. Гипотезы: Н0: Показатель социального интеллекта после тренинга коммуникативной компетентности не выше, чем до тренинга Н1: Показатель социального интеллекта после тренинга коммуникативной компетентности выше, чем до тренинга
Для каждой пары значений определить направление и значение сдвига d=xпосле-хдо. Результат вычисления записывается в таблицу. В соседний столбик записываются абсолютные значения сдвигов, то есть, знак не учитывается. Полученный ряд ранжируется, при этом нулевой сдвиг не ранжируется. Ранг числа записывается в следующий столбик
Проверим правильность ранжирования. Сложим все ранги и подсчитаем сумму рангов: 4,5+12,5+7+7+2+9,5+4,5+7+9,5+2+11+2+12,5=91.
Подсчитаем сумму рангов по формуле:
Обе величины совпали, 91=91, следовательно, ранжирование проведено правильно. Ориентируясь на знак сдвига, подсчитать суммы рангов соответствующие положительному направлению сдвигов T+ = Где R+ – ранговые значения сдвигов с положительным знаком; R- – ранговые значения сдвигов с отрицательным знаком.
T+ = T- = Эмпирическое значение критерия (Tэмп) соответствует меньшей из двух ранговых сумм, следовательно Tэмп=13,5. Общее количество сдвигов n=13, так как десять положительных сдвигов и три отрицательных сдвига. По таблице определяем критические значения критерия при данном количестве сдвигов. Для уровня статистической значимости р=0,05 критическое значение критерия Т0,05=21, для уровня статистической значимости р=0,01 критическое значение критерия Т0,01=12. Результаты вычисления представим наглядно.
Статистический вывод: так как рэмп<0,05, нулевая гипотеза Н0 отклоняется и принимается альтернативная гипотеза на уровне статистической значимости р<0,05. Психологический вывод: тренинг коммуникативной компетентности способствовал развитию социального интеллекта студентов (р<0,05).
Задания для самостоятельной работы № 5.1. На случайной выборке из 10 карликов проверялось действие некоторого стимулятора роста. Проверить гипотезу о том, что стимулятор существенно не меняет рост карликов из изучаемой совокупности.
№ 5.2. Ученики седьмого класса отмечали свое самочувствие (тест САН) до и после урока физкультуры. Достоверно ли изменение общего самочувствия школьников?
№ 5.3. В курсовом исследовании Л.Н.Кузьмина изучала влияние совместной творческой деятельности на развитие взаимоотношений в подростковом коллективе. В качестве показателей рассматривались уровень развития эмпатийных тенденций, измеряемый по методике И.М.Юсупова и изменение социально-психологического климата в коллективе. Результаты испытания представлены в таблице. Определите, подтвердилась ли гипотеза.
№ 5.4. Исследователя интересовала эффективность тренинга коммуникативной компетентности. Участники тренинга – студенты четвертого курса физико-математического факультета педвуза. Измерения проводились дважды - в первый день и в последний тренинга. В таблице представлены результаты самоактуализационного теста (САТ) для одной группы. Приняты следующие обозначения шкал: ориентация во времени (Tc); поддержки (I); ценностных ориентаций (SAV); гибкости поведения (Ex); сензитивности (Fr); спонтанности (S); самоуважения (Sr); самопринятия (Sa); представление о природе человека (Nc); синергии (Sy); принятии агрессии (A); контактности (C). На какие качества тренинг оказал наибольшее воздействие? Достоверно ли наблюдаемое изменение?
Первый замер
Второй замер
№ 5.5. Эффективность программы тренинга коммуникативной компетентности оценивалась через качество решения коммуникативных педагогических задач. Результаты испытания представлены в таблице. Достоверно ли, что участники тренинга стали более эффективно решать коммуникативные педагогические задачи?
№ 5.6. Можно ли говорить о достоверной тенденции в оценках?
№ 5.7. В таблице представлены изменение самооценки своего состояния в течении учебного года. Достоверны ли различия в самооценке своего состояния?
№ 5.8. В группе из 20 человек, имеющих повышенный уровень тревожности, 6 человек сообщили, что тревожность не изменилась, 14 человек сказали, что тревожность значительно снизилась. Из 20 человек, не имеющих проблем с тревожностью, 6 человека сообщили, что их тревожность повысилась, 14 человек не заметили каких-либо изменений с тревожностью. Проверьте эффективность коррекционной программы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 860; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.117.52 (0.011 с.) |


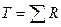
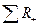 и T- =
и T- = 
 Фридмана
Фридмана
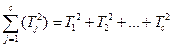
 ,
,






