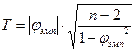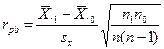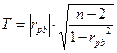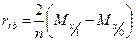Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент линейной ранговой корреляции кендаллаСодержание книги
Поиск на нашем сайте
Коэффициент Кендалла имеет те же свойства, что и коэффициент Спирмена. Коэффициент линейной ранговой корреляции Кендалла вычисляется по формуле:
где n-объем выборки P – общее число совпадений Q – общее число инверсий
Общее число совпадений (P) равно количеству значений, которые находятся правее и имеют ранги по «У» выше, чем у этой точки. Общее число инверсий равно количеству значений, находящихся правее, имеют по «У» ранги ниже, чем у этой точки. Критические значения определяются по таблице для t критерия Стьюдента. Для этого определяется эмпирическое значение критерия Стьюдента по формуле:
где τэмп – коэффициент корреляции, n – число коррелируемых признаков. Число степеней свободы n=n-2.
Коэффициент ассоциации Пирсона (j) Определяет силу связи признаков (переменных) измеряемых по дихотомической шкале наименований. Коэффициент ассоциации Пирсона вычисляется по формуле:
Для определения значений «a, b, c, d» строят таблицу сопряженности. Таблица сопряженности
где а – количество испытуемых имеющих «0» по Х и «1» по У b - количество испытуемых имеющих «1» по Х и «1» по У с - количество испытуемых имеющих «0» по Х и «0» по У d - количество испытуемых имеющих «1» по Х и «0» по У
Критические значения определяются по таблице для t критерия Стьюдента. Для этого определяется эмпирическое значение критерия Стьюдента по формуле:
где φэмп – коэффициент корреляции, n – число коррелируемых признаков. Число степеней свободы n=n-2. Точечный бисериальный коэффициент корреляции - rpb Уравнение представляет собой алгебраическое упрощение коэффициента корреляции Пирсона для случая, когда Y - дихотомическая переменная, X – в шкале интервалов или отношений. Точечный бисериальный коэффициент корреляции вычисляется по формуле:
где Х.1 – среднее по Х объектов, имеющих единицы по Y; X.0 - среднее по Х объектов, имеющих нуль по Y; σx – стандартное отклонение всех n значений по Х; n1 – число объектив, имеющих единицу по Y; n0 - число объектив, имеющих ноль по Y; n = n1 + n0, объем выборки
Поиск критических значений осуществляется по таблице для t-критерия Стьюдента. Эмпирическое значение критерия Стьюдента определяется по формуле:
где rpb – коэффициент корреляции, n – число коррелируемых признаков. Число степеней свободы n=n-2.
Рангово-бисериальный коэффициент - rrb Рангово-бисериальный коэффициент корреляции вычисляется по формуле:
где Mx|1- средний ранг объектов имеющих единицу по X, Mx|0- средний ранг объектов имеющих ноль по X, n – общее число объектов. Коэффициентыточечно-бисериальный и рангово-бисериальной корреляции изменяются в пределах [-1; +1]; как и в случае с коэффициентом j, отрицательный знак содержательной интерпретации в большинстве случаев не имеет.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.255.122 (0.007 с.) |

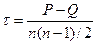
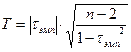
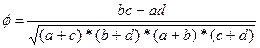 .
.