
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрические критерии различияСодержание книги
Поиск на нашем сайте
Параметрические критерии - критерии, включающие в формулу расчета параметры распределения: среднее арифметическое, дисперсию, стандартное отклонение. Ограничение в применении. Данные должны быть представлены в количественной шкале (интервальной, отношений). Распределение эмпирических данных должно соответствовать нормальному закону распределения. Данных должно быть достаточно много (n≥30). В сравнительных и лонгитюдных исследованиях популярна задача о различии двух выборочных средних, а также ряд сходных задач. Для ее решения чаще всего применяется t – критерий Стьюдента (псевдонимВ.Госсета). Этот критерий применяется в двух наиболее популярных вариантах – для независимых и зависимых выборок.
T – критерий Стьюдента для независимых выборок t = где х1 - среднее арифметическое значение 1-й выборки;
n1 – объем первой выборки (количество индивидуальных значений в первой выборке); число степеней свободы: n = n1 + n2 – 2
t – критерий Стьюдентадля зависимых выборок t =
где d – разность между результатами в каждой паре (d=хпосле-хдо); n – число пар данных (объем выборки). число степеней свободы: n = n – 1 или
где Оценка достоверности различий выборочной средней и генеральной средней В некоторых случаях значение генеральной средней известно, например оно может быть получено в процессе стандартизации психодиагностического теста с помощью весьма большой по объему, в несколько тысяч испытуемых, выборки стандартизации. Для этой цели используется формула:
Где
μ – генеральное среднее; ошибка репрезентативности n - объем выборки; число степеней свободы n = n – 1,
Например, в тесте Векслера, измеряющем уровень умственного развития, среднее значение генерального среднего
F- критерий Фишера Назначение. Определение достоверности или недостоверности различия двух выборочных дисперсий в сравниваемых выборках. Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух рядов наблюдений. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе.
df1 – число степеней свободы, df1 = n1 -1 n1 – объем первой выборки ( df2 – число степеней свободы, df2 = n2 -1 n2 – объем второй выборки (
Если выборки взяты из одной генеральной совокупности или из разных совокупностей с одинаковыми генеральными дисперсиями, то подтверждается нулевая гипотеза.
Примеры решения задач
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.56.125 (0.01 с.) |

 ,
, - дисперсия 1-й выборки;
- дисперсия 1-й выборки; ,
,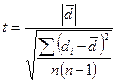 ,
, - среднее значение сдвигов.
- среднее значение сдвигов.
 - ошибка репрезентативности для генерального среднего;
- ошибка репрезентативности для генерального среднего; - выборочное среднее;
- выборочное среднее;
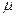 =100.
=100.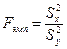
 ).
). ).
).


