Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные этапы построения гистограммыСодержание книги
Поиск на нашем сайте 1. Выбор числа разрядов 2. Определение ширины разряда 3. Нахождение границ разрядов 4. Вычисление числа переменных, попавших в каждый разряд, то есть частоты встречаемости переменных в разряде 5. Графическое изображение. Группировка данных Группировку данных выполняют в случаях, когда достаточно большой объем данных и большой диапазон разброса данных. Необходимо, чтобы массив группируемых данных имел объем N> 50 – 80. Целью группировки является получение эмпирической функции распределения, после чего уже по распределению вычисляются числовые характеристики. Для группировки необходимо, прежде всего, расположить данные каждой выборки в возрастающем порядке. Выделяют несколько способов группировки данных.
Способ 1. Формула Стержеса k = 1 + 3,3221* lg(N), где k – число интервалов; N – количество данных (объем выборки). Величина интервала (ширина интервала) группировки – λ определяется: λ = Величина интервала округляется до некоторого «удобного» числа. Как правило, округляют так, чтобы λ³Dx, где Dx – абсолютная погрешность измерения значений случайной величины Х в условиях эксперимента.
Способ 2. Число разрядов (k) выбирается произвольно, из принципа целесообразности. Гласс, Стенли рекомендуют от 8 до 12 разрядов. При выборе числа разрядов В.Х.Манеров предлагает руководствоваться следующими правилами: - число разрядов гистограммы должно быть нечетным (желательно, но не обязательно); - при большом объеме выборки N ≥100, число разрядов k = от 9 до 11-13; при N ≈ 25 – 40 рекомендуется k≈5; при N ≈ 40 – 90 рекомендуется k≈7;
Ширина разряда (ширина интервала) группировки – λ вычисляется: λ = Как правило, получаем не целое число, которое рекомендуется (не обязательно) округлять в сторону увеличения, так как в противном случае мы не захватим в верхние разряды крайние значения переменных. При таком округлении весь размах несколько увеличивается, и мы можем расширить его как в сторону больших, так и в сторону малых значений. Границы разрядов. Один из способов – сдвиг границ классов на половину последней варьирующей цифры (разряда). Так, если минимальное число равно 44, то границей первого разряда будет число 43,5.
Рекомендации по построению графиков (Л.В.Куликов)
1. График и текст должны взаимно дополнять друг друга 2. График должен быть понятен «сам по себе» и включать все необходимые обозначения, должен быть ясным и полным, отражающим содержание. 3. На одном графике не разрешается изображать больше четырех кривых. 4. Надписи на осях следует располагать внизу и слева. 5. Точки на разных линиях принято обозначать кружками, квадратами и треугольниками. 6. Надписи и легенда располагаются, как правило, в нижней или правой части диаграммы. 7. Цифры шкалы следует наносить слева и снизу или вдоль осей. Горизонтальную шкалу (по оси абсцисс) необходимо строить слева направо, вертикальную (по оси ординат) - снизу вверх. 8. Если числовые данные не включены в диаграммы, желательно их представить рядом в табличной форме. 9. Густота координатной сетки должна быть оптимальной, не затрудняющей чтения графика. 10. На графике допускается не более трех различных цветов. 11. Если графики отражают серию наблюдений, рекомендуется ясно обозначать все точки, соответствующие отдельным наблюдениям.
Задания для самостоятельной работы № 2.1. Построить полигон частот роста взрослых людей, родившихся в Англии в XIX веке. Построить гистограмму для сгруппированных данных.
№ 2.2. В опыте по изучению амплитудно-частотной характеристики руки человека-оператора для одного из испытуемых получены значения амплитуд установившихся колебаний руки, см. таблицу.
Значение амплитуды установившихся колебаний руки испытуемого (мм)
Определить эмпирическую функцию распределения (построить полигон частот и гистограмму); осуществить группировку данных; определить меры центральной тенденции.
№ 2.4. Провести первичную обработку: построить полигон частот, гистограмму, определить медиану, моду, среднее арифметическое.
№ 2.3. В таблице представлены результаты по тесту на усвоение кода, в котором производилась замена бессмысленных слогов из одного набора аналогичными элементами из другого набора. Число правильных ответов, данных испытуемым за две минуты, уложилось в переделах от 8 до 55.
Частотное распределение результатов у 1000 студентов по тесту усвоения кода (A.Anastasi, 1934).
Провести первичную обработку результатов: построить полигон частот, гистограмму по сгруппированным данным, определить медиану, моду, среднее арифметическое.
№ 2.5. Рассмотреть свойства среднего арифметического и дисперсии, решив задачу. Последовательно выполнить все три варианта. Для каждого варианта. Вычислите для каждой группы среднее арифметическое и дисперсию. Объедините первичные данные двух групп «А» и «В» и для объединенной выборки вычислите среднее арифметическое и дисперсию. А) Группа А: 1, 2, 2, 3, 3, 4; Группа В: 4, 5, 1, 3, 3, 3, 2, 2 Б) Группа А: 1, 2, 3, 3, 3, 5; Группа В: 4, 5, 1, 3, 3, 3, 2, 2 В) Группа А: 1, 2, 2, 3, 3, 4; Группа В: 5, 6, 7, 7, 8, 7, 9 Определите: А) как соотносятся средние арифметические трех групп; Б) как соотносятся дисперсии трех групп? В) зависит ли результат от объема выборки? Объяснить полученный результат. № 2.6. Экспериментально определены скорости, с которыми люди записывают цифры арабского алфавита. Вычислить по экспериментальным данным меры центральной тенденции, дисперсию, асимметрию и эксцесс.
№ 2.7. Особенности памяти изучались по методике А.Р. Лурия. Исследование проводилось в утреннее время. Студентам первого курса факультета психологии предъявлялись тринадцать слов. Провести первичную обработку полученных данных, построить полигон частот, гистограмму. Проверить соответствие полученного эмпирического распределения нормальному распределению. Группа А: 9, 11,9, 11, 13, 10, 8, 9, 10, 10, 10, 10 Группа Б: 9, 11,9, 11, 13, 10, 8, 9, 10, 10, 10, 10 Группа В: 11, 12, 7, 10, 11, 7, 9, 11, 10, 11, 11
№ 2.8. Провести первичную обработку результатов, построить полигон частот, гистограмму. Проверить соответствие эмпирического распределения нормальному распределению. Вычислить статистическую норму. Первичные данные: 7, 4, 2, 6, 3, 1, 5, 2, 5, 3, 6, 2, 4, 3, 2, 4, 4, 3, 2, 4, 3, 2, 3, 5, 2, 3. № 2.9. По методике А.Р. Лурия определялся объем кратковременной и долговременной памяти. В исследовании участвовали студенты второго курса факультета психологии. Студентам предлагался набор из десяти слов. Результаты исследования представлены в таблице. Построить полигон частот, гистограмму распределения частот, гистограмму накопленных частот, сглаженный график распределения частот. Определить меры центральной тенденции и меры изменчивости. Проверить полученное эмпирическое распределение на соответствие нормальному распределению.
№ 2.10. Исследовалась мотивация к успеху по методике Т.Элерса. Исследование проводилосьна базе факультета психологии. Участниками исследования являлись студенты первого курса. Объем выборки – 60 человек. Уровень мотивации к успеху определяется исходя из набранных баллов следующим образом: низкая мотивация - от 1 до 10 баллов; средний уровень - от 11 до 16 баллов; умеренно высокий уровень - от 17 до 20 баллов; слишком высокий уровень свыше 21 балла. Результаты измерения мотивации к успеху: 19, 18, 15, 13, 12, 16, 10, 14, 19, 10, 14, 15, 13, 14, 15, 14, 15, 13, 17, 16, 17, 19, 16, 16, 18, 20, 16, 13, 18, 17, 17, 14, 19, 14, 10, 17, 20, 15, 22, 13, 11, 15, 17, 21, 20, 18, 11, 12, 10, 17, 17, 17, 17, 11, 19, 19, 14, 19, 15, 18, 21. Провести первичную обработку полученных результатов, построить полигон частот, гистограмму. Проверить соответствие полученного эмпирического распределения нормальному распределению. Построить гистограмму по сгруппированным данным, где ось «Х» - уровень мотивации к успеху, ось «Y» - процент студентов имеющих данных уровень мотивации. № 2.11. Исследовалась мотивация к избеганию неудач по методике Т.Элерса. Исследование проводилосьна базе факультета психологии. Участники исследования - студенты первого курса. Объем выборки – 60 студентов. Уровень мотивации определяется исходя из набранных баллов. Чем больше сумма баллов, тем выше уровень мотивации к избеганию неудач, защите. Уровень мотивации определяется следующим образом: низкая мотивация к защите - от 2 до 10 баллов; средний уровень - от 11 до 16 баллов; высокий уровень - от 17 до 20 баллов; слишком высокий уровень мотивации к избеганию неудач, защите - свыше 20 баллов. Результаты измерения мотивации к избеганию неудач: 17, 18, 16, 16, 12, 13, 15, 14, 14, 13, 20, 11, 12, 4, 12, 5, 12, 22, 18, 6, 15, 17, 16, 15, 12, 6, 14, 20, 3, 17, 8, 19, 11, 5, 4, 15, 7, 19, 15, 13, 15, 18, 19, 18, 13, 3, 17, 10, 16, 14, 21, 18, 15, 20, 26, 10, 17, 13, 17, 18. Провести первичную обработку полученных результатов, построить полигон частот, гистограмму. Проверить соответствие эмпирического распределения нормальному распределению. Построить гистограмму по сгруппированным данным, где по оси «Х» откладывается уровень мотивации, по оси «Y» процент студентов имеющих данных уровень мотивации. № 2.12. В рамках дипломного исследования изучалась сформированность профессионально важных качеств будущих педагогов, влияющих на особенности педагогического общения. Выборку составили студенты первого и четвертого курса специальности «профессиональное образование» института профессионального образования и информационных технологий в количестве 62 человек. В качестве одного из показателей выступила эмпатия, которая измерялась по методике Бойко. Ниже приводятся результаты исследования. Первый курс: 26, 17,18, 18, 13, 16, 13, 12, 18, 16, 16, 15, 18, 16, 11, 13, 18, 21, 18, 18, 18, 16, 21, 20, 21, 18, 24, 14, 20. Четвертый курс: 14, 19, 26, 13, 22, 16, 23, 14, 16, 17, 24, 21, 23, 13, 23, 19, 23, 19, 15, 24, 23, 22, 24, 21, 22, 17, 22, 21, 13, 7, 16, 19, 23. Вычислить статистическую норму отдельно для каждого курса и для объединенной выборки. Влияет ли на результат объем выборки?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |


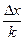 =
=