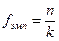Выявление различий в распределении признака

 

В психолого-педагогических исследованиях часто возникает задача сравнения распределений значения признака. Например, изменилась ли успеваемость школьников после введения новой программы обучения. Представив процентное распределение оценок до и после внедрения новой программы, мы сталкиваемся с задачей, а достоверно ли наблюдаемое изменение. Мы решаем задачу сравнения двух эмпирических распределений. Кроме необходимости сопоставления двух или нескольких эмпирических распределений признака между собой, часто возникает задача сопоставления эмпирического распределения признака с теоретическим.

Для решения данного круга задач часто применяют критерии c² – Пирсона или l - Колмогорова – Смирнова.

 

Критерий c² – критерий Пирсона

Критерий c² –Пирсона один из критериев, который наиболее часто применяют в психолого-педагогических исследованиях.

Данный критерий часто применяют для сопоставления распределений: эмпирического распределения с теоретическим (равномерным, нормальным и т.д.); сопоставления двух и более эмпирических распределений одного и того же признака друг с другом. Критерий используется также для определения взаимосвязей между признаками в таблицах сопряженности.

Исходные данные могут быть представлены в любой шкале, начиная со шкалы наименований. Выборки должны быть случайными и независимыми. Желательно, чтобы объем выборки был ≥20, с увеличением объема выборки точность критерия повышается. Теоретическая частота для каждого выборочного интервала не должна быть меньше 5.

Формула расчета эмпирического значения критерия:

 

c² = ,

где f_эj – j-е значение эмпирической частоты (наблюдаемой);

f_T – теоретическая частота (расчетная);

k – количество разрядов признака.

 

Количество разрядов признака – это возможные значения признака. Например, если мы сопоставляем распределения оценок, то разряды – это значения, которые может принимать оценка: «неудовлетворительно, «удовлетворительно», «хорошо», «отлично». Таким образом, разрядов четыре, k=4.

 

При сопоставлении эмпирического распределения с равномерным (теоретическим) распределением теоретические частоты рассчитываются по формуле:

Где, n – общее количество наблюдений;

k- количество разрядов признака.

 

При сопоставлении двух или более эмпирических распределений, теоретическая частота определяется для каждого значения эмпирической частоты:

Для удобства рекомендуется расчеты эмпирических частот представлять в таблице. Частоты встречаемости различных значений мы можем обозначить буквами.

Для нахождения критических значений критерия - c_кр, определяют число степеней свободы:

n = (k – 1)·(c - 1)

где, с – количество сравниваемых распределений;

k – количество разрядов признака

 

Для четырехклеточных матриц с общим числом испытуемых не более тридцати при расчетах величины c² рекомендуется вводить поправку Йетса на непрерывность. Поправка заключается в уменьшении разности между эмпирической и теоретической частотами, взятой по абсолютной величине, на 0,5 для каждой клетки таблицы: