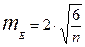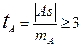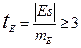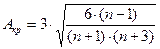Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное распределение и его свойстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кривую нормального закона распределения называют нормальной или гауссовой кривой. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. во Франции, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.
где u – высота кривой прямо над всяким заданным значением х на графике распределения частот; е – основание системы натуральных логарифмов = 2,718.., а и s - числа, которые определяют положение кривой относительно числовой оси и регулируют ее размах. График нормального распределения представляет собой так называемую колоколообразную симметричную кривую. Меняя значения а и s, можно сдвигать конкретную нормальную кривую по числовой оси вверх и вниз и менять ее размах. Величина a соответствует среднему распределения частот большой выборки (математическому ожиданию); s - стандартному отклонению этого распределения. Таким образом, параметр а (математическое ожидание) характеризует положение, а параметр s2 (дисперсия) – форму нормальной кривой. Нормальный закон распределения случайной величины с параметрами а=0, s2=1, т.е. N(0;1), называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Площадь ограниченная такой кривой равна = 1. Для совмещения любой нормальной кривой с единичной достаточно выполнить простое преобразование исходного распределения путем вычитания среднего значения
Нормальное распределение характеризуется тем, что крайние значения признака в нем встречаются достаточно редко, а значения близкие к средней величине - достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречается в естественно - научных исследованиях и казалось «нормой» всякого массового случайного проявления признака. Нормальная кривая всегда будет симметричной относительно а. Площадь между кривой и осью х равна 1. Свойства нормального теоретического распределения 1) мода, медиана и среднее арифметическое равны или имеют близкие по величине значения; 2) показатели асимметрии и эксцесса равны нулю, As=0 и Еs=0. 3) Выполняется правило трех сигм.
Правило трех сигм Общее для всех этих кривых: в любом нормальном распределении приблизительно:
1. 68% площади под кривой лежит в пределах одной s от среднего в любом направлении (то есть а ±1s); 2. 95% площади под кривой лежит в пределах двух s от среднего в любом направлении (то есть а±2s); 3. 99,7% площади под кривой лежит в пределах трех s от среднего в любом направлении (то есть а ±3s ). Правило трех сигм на языке теории вероятностей: P{÷X-mê<s} = F (1) = 0.6837 P{÷X-mê<2s} = F (2) = 0.9545 P{÷X-mê<3s} = F (3) = 0.9973 Вероятность того, что число Х попадает в интервал |X-mê<s равна 0,6837.
Правило трех сигм А) Если в симметричном распределении признака по обе стороны от выборочной средней отложить расстояние равное s, то оно будет включать 2/3 наблюдений (в нормальном распределении 68% наблюдений). Б) В интервале Х=[Хср± 2s] находится 95% наблюдений. В) В интервале Х=[Хср±3s] находится 99% наблюдений (в нормальном распределении 99,73% наблюдений).
Рис. 3. График нормированного нормального распределения признака.
Если для однородной выборки, полученные по заданной методике результаты подчиняются нормальному закону распределения, то среднее арифметическое Хср этих результатов и стандартное отклонение s результатов для выборки определяют границу статистической нормы [Хср±s].
Рис. 4. График нормального распределения признака Нормальность распределения результативного признака можно проверить путем расчета показателей асимметрии и эксцесса и сопоставления их с критическими значениями (критерий Н.А. Плохинского или Е.И. Пустыльника). Проверку соответствия эмпирического распределения нормальному, можно осуществить и по критерию χ2-Пирсона.
Критерий Н.А. Плохинского Вычисляются ошибки репрезентативности асимметрии и эксцесса:
где n -объем выборки Если показатели асимметрии и эксцесса превышают в три и более раз по абсолютной величине свою ошибку репрезентативности, то эмпирическое распределение отличается от нормального.
Критерий Е.И. Пустыльника Вычисляются критические значения асимметрии и эксцесса
где n -объем выборки Если эмпирические значения асимметрии и эксцесса больше своих критических значений As>Aкр и Es>Екр, то эмпирическое распределение отличается от нормального.
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1962; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.125 (0.009 с.) |


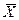 из каждого индивидуального балла Х i и деления на s.
из каждого индивидуального балла Х i и деления на s.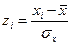 , z = 0, s=1.
, z = 0, s=1.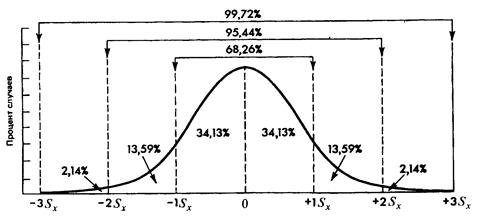

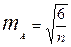 ;
;