
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика основных измерительных шкалСодержание книги
Поиск на нашем сайте
Шкала наименований (номинативная) – это шкала, классифицирующая по названию: nomen (лат.) – имя, название. Шкала наименований получается путем присвоения «имен» объектам. Принцип классификации – по названию. При этом, нужно разделит множество объектов на непересекающиеся множества. Название не измеряет количественно, оно лишь позволяет отличить один объект от другого. Шкала наименований (номинативная) – это способ классификации объектов или субъектов, распределения их по ячейкам классификации. Расклассифицировав все объекты по ячейкам классификации, мы получаем возможность от наименований перейти к числам, подсчитав количество наблюдений в каждой из ячеек. Номинативная шкала позволяет подсчитать частоты встречаемости разных «наименований», или значений признака, и затем работать с этими частотами с помощью математических методов. Единица измерения в данной шкале – количество наблюдений или частота. Простейший случай номинативной шкалы – дихотомическая шкала, состоящая всего лишь из двух ячеек. Математические и статистические величины, вычисление которых допустимо на данном уровне: относительная частота, мода, процент, доли, коэффициент корреляции φ, критерий c2. Шкала порядка (порядковая, ранговая, ординальная) предназначена для измерения (обозначения) степени различия какого-либо признака или свойства у разных объектов. Порядковая шкала - это шкала, классифицирующая по принципу «больше – меньше». Порядковые шкалы дают возможность оценить степень выраженности признака. В порядковой шкале должно быть не менее трех классов с установленной последовательностью не допускающей перестановку. В порядковой шкале не известно истинное расстояние между классами, известно лишь, что они образуют последовательность. От классов легко перейти к числам, если мы условимся считать, что низший класс получает ранг 1, средний – ранг 2, а высший – ранг 3. Чем больше классов в шкале, тем больше возможностей для математической обработки полученных данных. Единица измерения в данной шкале - расстояние в один класс или ранг. Все психологические методы, использующие ранжирование, построены на применении шкалы порядка. Математические и статистические величины, вычисление которых допустимо на данном уровне: мода, медиана, процентили, непараметрическая статистика. Интервальная шкала – это шкала, классифицирующая по принципу «больше на определенное количество единиц – меньше на определенное количество единиц». Каждое из возможных значений признака отстоит от другого на равном расстоянии. Основная особенность - произвольность выбора нулевой точки на шкале, которая не указывает на полное отсутствие измеряемого свойства, то есть, нет естественной точки отсчета. Единицей измерения является расстояние в одно измерение. Ячейки находятся друг от друга на равном расстоянии. Порядок расположения ячеек - последовательность от нуля до самого большого значения и наоборот. Математические и статистические величины, вычисление которых допустимо на данном уровне: методы непараметрической и параметрической статистики Шкала равных отношений – это шкала, классифицирующая объекты пропорционально степени выраженности измеряемого признака. В шкалах отношения классы обозначают числами, которые пропорциональны друг другу: 2 так относится к 4, как 4 к 8. Это предполагает наличие абсолютной нулевой точки отсчета. Единица измерения в данной шкале - количество наблюдений или частота. Математические и статистические величины, вычисление которых допустимо на данном уровне: любые математические операции. Правило ранжирования 1. Построить вариационный ряд (расположить данные первичного ряда в порядке возрастания) 2. Пронумеровать значения вариационного ряда, начиная с меньшего значения. Меньшему значению присваивается первый номер 3. Рядом со значением записать его ранг, при этом: а) если значение в вариационном ряду встречается единственный раз, то ранг равен порядковому номеру; б) если значение в вариационном ряду встречается два или более раз, то ранг вычисляется как среднее из порядковых номеров, которые присвоены этому значению. 4. Правильность ранжирования можно проверить. Сумма рангов должна совпадать с расчетной: где N – количество значений в ранжируемом вариационном ряду.
Пример ранжирования. Индивидуальные значения переменной «Х»: 2, 5, 6, 2, 5, 1, 3, 4, 4, 4. Вариационный ряд «Х»: 1, 2, 2, 3, 4, 4, 4, 5, 5, 6 Данные вариационного ряда нумеруются. Определяется ранг значения, при этом, меньшему значению присваивается ранг равный единице. Значение «1» встречается в вариационном ряду единственный раз и имеет порядковый номер равный «1». Поэтому ранг значения «1» равен порядковому номеру, то есть R(1)=1. Значение «2» встречается в вариационном ряду два раза. Поэтому, ранг значения «2» вычисляется как среднее из порядковых номеров, на которых располагается это значение. R(2)= Значение «3» в вариационном ряду встречается единственный раз, поэтому ранг равен порядковому номеру. Ранг значения «3» равен четырем, то есть R(3)=4.
Сумма рангов должна совпадать с расчетной:
Процентиль – это процентная доля индивидов из выборки стандартизации, первичный результат которых ниже данного первичного показателя. Процентили показывают относительное положение каждого индивида в нормативной выборке, а не величину различия между результатами. 99 возможных процентилей (Р1,..Р99) делят множество наблюдений на 100 частей с равным числом наблюдений в каждой. Например, если 28% людей правильно решают 15 задач в тесте на арифметическое мышление, то первичному показателю 15 соответствует 28-й процентиль (Р28). Р-й процентильпредставляет собой точку, ниже которой лежит Р% оценок. 50-й процентиль (Р50) соответствует медиане. Процентили выше 50 представляют показатели выше среднего, а те, которые лежат ниже 50, - сравнительно низкие показатели. Процентили указывают на относительное положение индивида в выборке стандартизации. Их также можно рассматривать как ранговые градации, общее число которых равно 100, с той разницей, что при ранжировании принято начинать отсчет сверху, то есть с лучшего члена группы, получающего ранг 1. В случае процентилей отсчет ведется снизу, так что, чем ниже процентиль, тем хуже позиция индивида. Процентили не следует смешивать с обычными процентными показателям. Последние являются первичными показателями и представляют собой процент правильно выполненных заданий, тогда как процентиль – это производный показатель, указывающий на долю от общего числа членов группы. Первичный результат, который ниже любого показателя, полученного в выборке стандартизации, имеет нулевой процентильный ранг (Р0). Результат, превышающий любой показатель в выборке стандартизации, получает процентильный ранг 100 (Р100). Эти процентили, однако, не означают нулевого или абсолютного выполнения теста. Перед началом вычисления любого процентиля в группе оценок надо упорядочить эти оценки по возрастанию. Для больших групп это непроизводительно и удобнее использовать сгруппированные данные. Общая формула определения Рр -го процентиляв группе n оценок
L - фактическая нижняя граница единичного интервала оценок, содержащего частоту p * n снизу распределения. (cumf) - накопленная к L частота, f - частота интервала оценок, содержащего частоту p*n. W – ширина интервала оценок Накопленные частоты к любой заданной оценке представляют собой суммарное количество частот на этой оценке или ниже ее.
f - частота интервала оценок, содержащего частоту pn
Переход в шкалу Т-баллов: Где, xi-индивидуальное (i-е значение);
Задания для самостоятельной работы № 1.1. Определите в какой шкале представлены ниже приведенные измерения и обоснуйте свое решение. 1) месяц в календарном году; 2) температура, представленная в шкале Цельсия; 3) измеренное по шкале Кельвина значение температуры; 4) значение коэффициента интеллекта – IQ; 5) измерение роста (см); 6)измерение веса (кг); 7) 50-й процентиль; 8) оценка за успеваемость в журнале; 9) порядковый номер на майке футболиста; 10) порядковый номер в списке (для его идентификации); 11) упорядочивание участников исследования по времени решения задач; 12) время решения задачи. №1.2. Дайте характеристику каждой из четырех шкал.Заполните таблицу.
№ 1.3. Придумайте свои примеры измерений производимых в шкале наименований, порядка, интервальной и отношений. Обоснуйте выбор шкал.
№ 1.4. У детей, поступающих в первый класс отметки вербального мышления, имели следующие значения: ВМ = 17, 10, 29, 16, 3, 14, 9, 26, 6, 11, 10, 12, 19. Представить данные в шкалах: наименования, порядка, интервальной. Считать, что если ВМ < 12, то ребенок определяется в подготовительную группу и ему присваивается код = 0, иначе – присваивается код = 1. Данные представить в виде таблицы.
№ 1.5. Из сборника психологических тестов выберите 5-6 методик (например, тест Русалова – ОСТ, Айзенка и др.). Для каждой методики определите: в какой шкале осуществляется сбор эмпирических данных, в какой измерительной шкале будет представлен результат, полученный по методике. Результаты работы оформить в виде таблицы:
№ 1.6. Определитетип шкалы: а) уровень развития психических процессов: высокий уровень – Андреев; средний уровень – Прохоров; низкий уровень – Борисов. б) рост Иванов – рост 180 см; Петров – рост 164 см; Сидоров – рост 172 см; в) тип темперамента - сангвиник; флегматик; меланхолик; холерик.
№ 1. 7. Представить индивидуальные значения в шкале рангов. а) 3,1,5,2,7,5,9,10,12, 5, 9 б) 2,1,3,2,5,4,6,7,7,9,10,10,11,8,16 в) 3, 16, 20,5,20,5,8,1,30,22,10,12,4,11,4, 9 г) 12, 5, 5, 2, 2, 12, 7, 2, 7, 9, 15, 19, 18, 14
№ 1.8. Преподаватель предложил 125 учащимся контрольное задание, состоящее из 40 вопросов. В качестве оценки теста выбиралось количество вопросов, на которые были получены правильные ответы. Негрупповое распределение 125 оценок теста приводится в таблице.
а) Каков 25-й процентиль в группе 125 оценок теста, т.е. чему равна величина Р25. (Р25 - это точка ниже которой лежит 25%, из 125 оценок). б) Каков 50-й процентить; в) Каков 75-й процентить.
№ 1.9. Вычислите процентильные ранги.
№ 1.10. Определить 25-й, 50-й и 75-й процентиль. Вычислить процентильные ранги. Первичные данные: 2, 3, 4, 3, 5, 6, 7, 5, 7, 6, 8, 9, 8, 15, 10, 11, 3, 12, 8, 14, 12, 17, 18, 20, 10, 17, 16, 15, 15, 14, 9, 11, 10, 9, 12, 4, 10, 9, 8, 14, 16, 15, 9, 11, 12, 15, 6, 10, 14, 10, 9, 14, 9, 11, 5, 12, 16, 7, 9, 11, 12, 17, 9, 10, 16.
№ 1. 11. Перевести показатели в Т-шкалу А) 2, 2, 4,4, 3, 3, 5, 5, 4, 3, 4, 6, 6, 6, 5, 7, 5, 7, 5, 6, 7, 8, 8; Б) 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 6; В) 10, 12, 13, 13, 13, 14, 14, 14, 15, 15, 15, 16, 19. ОПИСАТЕЛЬНАЯ СТАТИСТИКА Описательная статистика - позволяет описывать, подытоживать и воспроизводить в виде таблиц и графиков данные того или иного распределения, вычислять среднее для данного распределения, его размах и дисперсию. Распределением признака называется закономерность встречаемости разных его значений. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может быть задан в виде таблицы, графика или формулы. Вариационный ряд – ряд данных представленных в порядке возрастания (убывания) признака. Статистическим рядом называется ряд данных, расположенных в порядке возрастания или убывания с соответствующими им весами (частотами или частостями). Вариационный и статистический ряды являются статистическими аналогами распределения признака (случайной величины Х). Параметры распределения - это его числовые характеристики, указывающие, где в «среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Наиболее важными параметрами являются математическое ожидание, дисперсия, показатели асимметрии и эксцесса. В реальных психологических исследованиях мы оперируем не параметрами, а их приближенными значениями, так называемыми оценками параметров. Это объясняется ограниченностью обследованных выборок. Чем больше выборка, тем ближе может быть оценка параметра к его истинному значению.
Меры центральной тенденции – характеристики совокупности переменных (признаков) указывающие на наиболее типичный, репрезентативный для изучаемой выборки результат. К мерам центральной тенденции относятся среднее арифметическое, мода, медиана. Мода (Мо) – наиболее часто встречаемое значение вариационного ряда. Варианты определения моды: 1. Если в вариационном ряду лишь одно значение встречается наиболее часто, то мода равна этому значению (варианте). 2. Если два соседних значения имеют одинаковую частоту и эта частота больше частот других значений, то мода вычисляется как среднее арифметическое из этих двух значений. 3. Если два наиболее часто встречаемых значения находятся не рядом, между ними есть значение с меньшей частотой встречаемости, то распределение имеет две моды (бимодальное распределение). Медиана (Ме) – значение вариационного ряда, делящее этот ряд на две равные части, так что количество значений справа от медианы, равно количеству значений слева от медианы. Место, (порядковый номер) на котором находиться медиана, можно рассчитать по формуле: NMe = где n – количество значений в вариационном ряду.
Если место, на котором должна находиться медиана, число целое, то медиана равна значению, которое находится на этом расчетном месте. Если расчетное место (порядковый номер значения) на котором должна находиться медиана число дробное, то медианы вычисляется как среднее арифметическое из двух значений, находящихся справа и слева от вычисленного места медианы.
Пример №1. В вариационном ряду нечетное число значений, n=9.
Место, на котором располагается медиана, вычисляется: NMe = На пятом месте в вариационном ряду располагается число «3». Таким образом, медиана равна трем, Me=3. Мы видим, что слева от медианы располагается четыре значения (1, 2, 2, 3) и справа от медианы также располагается четыре значения (4, 4, 4, 5).
Пример №2. В вариационном ряду четное число значений.
Место, на котором располагается медиана, вычисляется: NMe=(10+1)/2=5,5. Расчетное место, на котором должна находиться медиана, число дробное. Это место располагается между порядковыми номерами 5 и 6. В вариационном ряду на этом дробном месте нет значения. Поэтому, медиана рассчитывается как возможное значение переменной «Х», которое могло бы располагаться на этом расчетном месте. Медиана рассчитывается как среднее арифметическое из двух значений, которые располагаются слева и справа от расчетного места. На пятом месте располагается число три, на шестом месте число четыре, поэтому медиана Me=(3+4)/2=3,5. Таким образом, мы видим, что слева от медианы располагается пять значений (1, 2, 2, 3, 3) и справа от медианы также располагается пять значений (4, 4, 4, 5,6).
Среднее арифметическое является оценкой математического ожидания. Среднее арифметическое: где xi - каждое наблюдаемое значение признака; i - индекс, указывающий на порядковый номер данного значения признака; n – объем выборки;
Меры изменчивости – статистические показатели вариации (разброса) признака (переменной) относительно среднего значения, степени индивидуальных отклонений от центральной тенденции распределения. К мерам изменчивости относятся: вариационный размах, дисперсия, стандартное отклонение.
Вариационный размах: W = xmax - xmin характеризует ширину вариационного ряда.
Дисперсия (выборочная)(S2) Стандартное отклонение(s)
Дисперсия (выборочная)(S2) Стандартное отклонение(s)
Особенности эмпирического распределения описываются при помощи таких показателей как асимметрия и эксцесс. Асимметрия характеризует сдвиг эмпирического распределения относительно нормального теоретического распределения. Эксцесс характеризует островершинность распределения. Показатель асимметрии (Аs) рассчитывается по формуле:
Графики распределения случайной величины «х», с различными показателями асимметрии представлены на рисунке 2.
Рис.1. Графики трех распределений признака, которые отличаются по показателю асимметрии.
На рисунке представлены три распределения, различающиеся по знаку асимметрии. Распределение 1 характеризуется положительной асимметрией (левосторонней), распределение 2 – отрицательной (правосторонней), распределение 3 – нормальное распределение. Для симметричных распределений (нормального распределения) показатель асимметрии равен нулю, Аs=0. В случае, когда какие-либо причины способствуют преимущественному появлению средних или близких к средним значений, образуется распределение с положительным эксцессом. Если в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двувершинное. Показатель эксцесса (Еs) рассчитывается по формуле:
Графики распределения случайной величины «х», с различными показателями эксцесса представлены на рисунке 2.
Рис.2. Виды распределений признака с различными показателями эксцесса.
На рисунке 2 представлены три различных распределения признака. Распределение 1 характеризуется меньшим диапазоном вариативности и меньшей дисперсией, эксцесс данного распределения больше нуля Es>0. В распределении 1 чаще встречаются значения признака близкие к среднему. В распределении 2 чаще встречаются более высокие и более низкие, чем среднее значение признака, эксцесс данного распределения меньше нуля Es<0. Распределение 3 – нормальное распределение, эксцесс равен нулю.
Коэффициент вариации
Если коэффициент вариации высок, то, как правило, это свидетельствует о неоднородности значений признака.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1975; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.012 с.) |



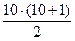 =1+2,5+2,5+4+6+6+6+4,5+4,5+10
=1+2,5+2,5+4+6+6+6+4,5+4,5+10


 - среднее арифметическое; σ-стандартное отклонение.
- среднее арифметическое; σ-стандартное отклонение. ,
,
 - знак суммирования.
- знак суммирования. , n<30.
, n<30.  , n<30.
, n<30. , n>30.
, n>30.  , n>30.
, n>30.
 - среднее арифметическое
- среднее арифметическое






