
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение модуля сдвига стали динамическим методомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте КРАТКАЯ ТЕОРИЯ. Под влиянием внешних сил всякое тело изменяет свою форму и размеры, т.е. деформируется. Упругой называется деформация, исчезающая с прекращением действия силы. Существуют различные типы деформации: растяжение (сжатие), сдвиг, кручение.
Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно. Так как угол мал, формулу можно записать в виде:
где СС1= ΔX- абсолютный сдвиг, γ - угол сдвига, называемый также относительным сдвигом, выражается в радианах. По закону Гука относительный сдвиг γ пропорционален касательному напряжению F/S, где S - площадь поверхности грани ВС, т.е.
где N - модуль сдвига:
Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном единице (при условии, что закон Гука выполняется). Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол φ - угол кручения. По закону Гука:
Модуль кручения f показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад.
Поэтому расчет деформации кручения может быть сведен к расчету деформации сдвига. Приведем без вывода соотношение, существующее между модулем кручения f и модулем сдвига N материала проволоки
где r, l - соответственно радиус и длина проволоки. Модуль кручения зависит не только от материала, но и от геометрических размеров проволоки. Из формулы (6) имеем
Таким образом, модуль сдвига материала можно найти, зная модуль кручения, радиус и длину проволоки.
Если колеблющиеся тела совершают вращательное движение, то к ним может быть применен основной закон динамики вращательного движения:
где М - вращающий момент относительно оси АВ, J - момент инерции тела относительно той же оси, Учитывая (4) и (8) можно переписать в виде:
Знак минус говорит о том, что вращающий момент сдвига направлен так, чтобы уменьшить угловое отклонение. Таким образом, тело совершает гармонические колебания, периоды которых можно найти из условия, что множитель пропорциональности между
Откуда
где Т - период колебания маятника. Чтобы найти f, необходимо исключить неизвестный момент инерции J. Для этого в задаче определяются два периода колебаний маятника. Используя возможность передвижения груза Р на рейке установки, меняем расстояние от оси вращения. В соответствии с l1 и l2 получаем моменты инерции J1 и J2.
где J0 - момент инерции рейки крутильного маятника. Периоды колебаний будут соответственно равны:
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА изображена на рис. 4. Крутильный маятник представляет собой стальной цилиндр Ц с двумя стержнями С, подвешенный с помощью двух стальных проволок к неподвижному кронштейну К. Момент инерции маятника J можно изменять перемещая вдоль стержней одинаковые стальные цилиндры m. ЗАДАНИЕ 1. Измерить L1, L2 и радиус проволоки r. 2. Снять зависимость Т периода полного колебания крутильного маятника от 3. Результаты эксперимента занести в таблицу.
4. Используя соотношения:
5.Результаты вычислений занести в таблицу.
6.Результат эксперимента представить в виде
ЛАБОРАТОРНАЯ РАБОТА № 2т
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1384; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

 Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 1).
Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 1). (1)
(1) , (2)
, (2) . (3)
. (3) . (4)
. (4) В результате деформации кручения возникает перекос образующих цилиндрической поверхности стержня (рис. 2), причем
В результате деформации кручения возникает перекос образующих цилиндрической поверхности стержня (рис. 2), причем (5)
(5)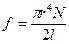 (6)
(6) (7)
(7) Динамический метод измерения модуля кручения основан на зависимости периода Т крутильных колебаний маятника, подвешенного на проволоке, от упругих свойств материала проволоки. Крутильным маятником служит рейка К с надетыми на нее цилиндрическими грузами Р, подвешенная на проволоке длиной L,радиусом r (см. рис. 3).
Динамический метод измерения модуля кручения основан на зависимости периода Т крутильных колебаний маятника, подвешенного на проволоке, от упругих свойств материала проволоки. Крутильным маятником служит рейка К с надетыми на нее цилиндрическими грузами Р, подвешенная на проволоке длиной L,радиусом r (см. рис. 3). (8)
(8) - угловое ускорение.
- угловое ускорение.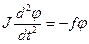 (9)
(9) и φ в уравнении (9) в данном случае 1/J должен быть равен:
и φ в уравнении (9) в данном случае 1/J должен быть равен: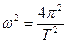 , т.е.
, т.е. 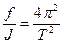 .
. , (10)
, (10) ,
,  , (11)
, (11) , Þ
, Þ  . (12)
. (12) Решая совместно два последних уравнения, получим формулу для расчета модуля кручения проволоки крутильного маятника:
Решая совместно два последних уравнения, получим формулу для расчета модуля кручения проволоки крутильного маятника: . (13)
. (13) момента инерции измеряя время t 50 полных колебаний.
момента инерции измеряя время t 50 полных колебаний. , мм
, мм
 ,
,  кг/м3, m =0,64 кг,
кг/м3, m =0,64 кг,  =3,4,
=3,4, 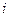 =1.2, вычислить Nji. Оценить погрешность измерения модуля сдвига стали.
=1.2, вычислить Nji. Оценить погрешность измерения модуля сдвига стали. Н/м2.
Н/м2.


