
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента поверхностного натяжения жидкости методом измерения максимального избыточного давления в пузырьках воздухаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КРАТКАЯ ТЕОРИЯ. Важнейший признак жидкости - существование свободной поверхности. Молекулы поверхностного слоя жидкости, имеющего толщину порядка 10-9м, находятся в ином состоянии, чем молекулы в толще жидкости. Поверхностный слой оказывает на жидкость давление, называемое молекулярным, что приводит к появлению сил, которые называются силами поверхностного натяжения.
Коэффициент поверхностного натяжения зависит от природы жидкости. Для каждой жидкости он является функцией температуры и зависит от того, какая среда находится над свободной поверхностью жидкости.
Микроманометр состоит из двух сообщающихся сосудов, один из которых представляет собой чашку большого диаметра, а другой наклонную стеклянную трубку малого диаметра (2-3 мм) (рис. 2). При достаточно большом отношении площадей сечений чашки и трубки можно пренебречь изменением уровня в чашке. Тогда по уровню жидкости в трубке малого диаметра можно определить измеряемую величину разности давлений:
где В начальный момент времени, когда давление воздуха над поверхностью жидкости в капилляре и сосуде В одинаково и равно атмосферному. Уровень смачивающей жидкости в капилляре выше, чем в сосуде В, а уровень несмачивающей – ниже, так как смачивающая жидкость в капилляре образует вогнутый мениск, а несмачивающая - выпуклый.
где Смачивающая капилляр жидкость поднимается до тех пор, пока гидростатическое давление столбика жидкости высотой
где
Если, повернув кран аспиратора А, медленно выпускать из него воду, то давление воздуха в аспираторе, в соединенных с ним сосуде В и наклонном колене микроманометра начнет уменьшаться. В капилляре же над поверхностью жидкости давление равно атмосферному. В результате увеличивающейся разности давлений мениск жидкости в капилляре будет опускаться, сохраняя кривизну, пока не опустится до нижнего конца капилляра (рис. 3б). В этот момент давление воздуха в капилляре будет равно:
С этого момента начинает меняться кривизна мениска. Давление воздуха в аспираторе и сосуде В продолжает уменьшаться. Так как разность давлений Из сказанного выше следует, что:
где
где Из формул (1) и (2) получим:
Так как глубина погружения капилляра в жидкость ничтожна
где В качестве манометрической жидкости в микроманометре используется вода ( ИЗМЕРЕНИЯ. 1. Налить в аспиратор воду до метки и закрыть его. Добиться равенства давлений в обоих коленах микроманометра, для чего на короткое время извлечь кран К. Установить его в такое положение, в котором он соединяет сосуд с аспиратором. 2. Открыть кран аспиратора настолько, чтобы изменение давления происходило достаточно медленно. Пузырьки воздуха должны отрываться примерно через каждые 10-15 с. После установления указанной частоты образования пузырьков можно проводить измерения. ЗАДАНИЕ. 1. С помощью термометра определить и записать комнатную температуру t. 2. Девять раз определить максимальное смещение уровня жидкости в наклонном колене микроманометра. Для расчета коэффициента поверхностного натяжения взять среднее значение Нср. 3. Аналогично определить коэффициент поверхностного натяжения этилового спирта. 4. Найти предельные абсолютную и относительную погрешности при определении поверхностного натяжения каждой жидкости. Записать для каждой жидкости окончательные результаты измерений с учетом их точности по формуле:
где 5. Сравнить полученные значения коэффициента поверхностного натяжения с табличными. РЕЗУЛЬТАТЫ t =, a = 300.
ЛАБОРАТОРНАЯ РАБОТА № 2э ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ КРАТКАЯ ТЕОРИЯ. Электрическим током называется упорядоченное (направленное) движение заряженных частиц. Сила тока – физическая величина, показывающая заряд, проходящий через поперечное сечение проводника за единицу времени:
Один из основных законов цепей постоянного тока - закон Ома для однородного участка цепи: величина тока прямо пропорциональна разности потенциалов (напряжению) на концах проводника и обратно пропорциональна сопротивлению проводника:
где R - сопротивление, которое, как показал Ом, прямо пропорционально длине проводника l и обратно пропорционально площади его поперечного сечения S:
где коэффициент 1 Ом = 1 В/1 А. Электрическое сопротивление проводника зависит от его температуры. У металлов оно возрастает при нагревании проводника, у электролитов уменьшается. В довольно широком интервале температур сопротивление металлических проводников является линейной функцией температуры T:
где R0 - сопротивление при 273 К (00 С), R - сопротивление при температуре T=T0 +D T, a - температурный коэффициент сопротивления. Возможны три способа соединения проводников: 1) последовательное, 2) параллельное, 3) комбинированное. При последовательном соединении n проводников сопротивлением Ri каждый общее напряжение, сила тока и сопротивление на участке цепи определяется в виде:
при параллельном:
где Ui, Ii, Ri – напряжение, сила тока и сопротивление для соответствующего проводника.
Если потенциалы точек С и D одинаковы, ток через гальванометр равен нулю. Это происходит при соответствующем выборе сопротивлений R1, R2, R3, когда:
Из соотношения (1), отображающего баланс моста, следует возможность измерения неизвестного сопротивления Rx:
Обычно в качестве сопротивления R3 используют магазин образцовых сопротивлений. Для балансировки моста подбирают в магазине сопротивлений такое сопротивление R=R3, при котором ток в гальванометре будет равен нулю. При этом достигается наибольшая точность. Выражение (2) упрощается, и искомое сопротивление становится численно равно сопротивлению R, набранному в магазине сопротивлений:
ИЗМЕРЕНИЯ Часть 1. Собрать измерительную цепь (рис. 1). Подключить к зажимам «а» и «б» неизвестное сопротивление Rx1, подбирая сопротивление (в магазине сопротивлений) добиться нулевого показания гальванометра. Записать полученный результат в таблицу. Часть 2. Определить сопротивление электрической лампочки, включенной в осветительную сеть ("горячей" лампочки). Для этого собрать и проверить электрическую цепь (рис. 2). (Внимание! Без разрешения преподавателя или лаборанта электрическую цепь в сеть не включать). Записать показания вольтметра U и амперметра I в таблицу и, по закону Ома для участка цепи, рассчитать сопротивление лампочки в горячем состоянии Rt по формуле:
где напряжение U берется в вольтах, ток I - в амперах, сопротивление R - в омах. ЗАДАНИЕ. 1.Измерить сопротивления двух резисторов (Rx1 и Rx2) порознь с помощью моста постоянного тока. Результаты занести в таблицу. 2.Измерить сопротивление тех же резисторов соединенных первый раз последовательно, а второй раз параллельно и сравнить значения, найденные из опыта с рассчитанными по формулам:
3. Определить относительную погрешность измерения:
4. Определить сопротивление электрической лампочки в горячем состоянии
5. Рассчитать температуру T нити накала лампочки согласно формуле:
где Для вольфрама a =5.1×10-3 К-1.
ЛАБОРАТОРНАЯ РАБОТА № 3э
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.205.182 (0.013 с.) |

 Силы поверхностного натяжения в любой точке поверхности направлены по касательной к ней и по нормали к любому элементу линии, мысленно проведенной на поверхности жидкости. Коэффициент поверхностного натяжения
Силы поверхностного натяжения в любой точке поверхности направлены по касательной к ней и по нормали к любому элементу линии, мысленно проведенной на поверхности жидкости. Коэффициент поверхностного натяжения 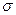 - физическая величина, показывающая силу поверхностного натяжения, действующую на единицу длины линии, разделяющей поверхность жидкости на части:
- физическая величина, показывающая силу поверхностного натяжения, действующую на единицу длины линии, разделяющей поверхность жидкости на части: .
.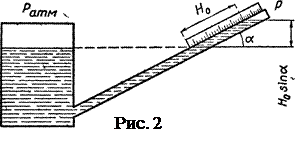 ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Экспериментальная установка изображена на рис. 1. Она состоит из аспиратора А, соединенного с микроманометром М и сосудом В, в котором находится исследуемая жидкость. В аспиратор наливается вода. С помощью крана К аспиратор А может отсоединяться от сосуда В и присоединяться к такому же сосуду С с другой исследуемой жидкостью. Сосуды В и С плотно закрываются резиновыми пробками, имеющими по отверстию. В каждое отверстие вставляется стеклянная трубочка, конец которой представляет собой капилляр. Капилляр погружается на очень малую глубину в жидкость (так, чтобы он только касался поверхности жидкости). Микроманометр измеряет разность давления воздуха в атмосфере и аспираторе, или, что то же самое, в капилляре и сосуде В или С.
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Экспериментальная установка изображена на рис. 1. Она состоит из аспиратора А, соединенного с микроманометром М и сосудом В, в котором находится исследуемая жидкость. В аспиратор наливается вода. С помощью крана К аспиратор А может отсоединяться от сосуда В и присоединяться к такому же сосуду С с другой исследуемой жидкостью. Сосуды В и С плотно закрываются резиновыми пробками, имеющими по отверстию. В каждое отверстие вставляется стеклянная трубочка, конец которой представляет собой капилляр. Капилляр погружается на очень малую глубину в жидкость (так, чтобы он только касался поверхности жидкости). Микроманометр измеряет разность давления воздуха в атмосфере и аспираторе, или, что то же самое, в капилляре и сосуде В или С. ,
, - плотность манометрической жидкости;
- плотность манометрической жидкости;  - расстояние принимаемого неизменным уровня жидкости в чашке до уровня в трубке по наклону трубки;
- расстояние принимаемого неизменным уровня жидкости в чашке до уровня в трубке по наклону трубки;  - угол, образованный наклонной трубкой с плоскостью горизонта.
- угол, образованный наклонной трубкой с плоскостью горизонта. Молекулярное давление под выпуклой поверхностью жидкости больше, а под вогнутым - меньше относительно давления под плоской поверхностью. Молекулярное давление, обусловленное кривизной поверхности, принято называть избыточным капиллярным давлением (давление Лапласа). Избыточное давление под выпуклой поверхностью считается положительным, под вогнутой - отрицательным. Оно всегда направлено к центру кривизны сечения поверхности, т.е. в сторону ее вогнутости. В случае сферической поверхности избыточное давление можно вычислить по формуле:
Молекулярное давление под выпуклой поверхностью жидкости больше, а под вогнутым - меньше относительно давления под плоской поверхностью. Молекулярное давление, обусловленное кривизной поверхности, принято называть избыточным капиллярным давлением (давление Лапласа). Избыточное давление под выпуклой поверхностью считается положительным, под вогнутой - отрицательным. Оно всегда направлено к центру кривизны сечения поверхности, т.е. в сторону ее вогнутости. В случае сферической поверхности избыточное давление можно вычислить по формуле: ,
, - радиус сферической поверхности.
- радиус сферической поверхности. (рис. 3а) не уравновесит избыточного давления, направленного в этом случае вверх. Высота
(рис. 3а) не уравновесит избыточного давления, направленного в этом случае вверх. Высота 
 ,
, - ускорение свободного падения, т.е.
- ускорение свободного падения, т.е. .
.
 где
где  - давление воздуха в сосуде В,
- давление воздуха в сосуде В,  - глубина погружения капилляра в жидкость,
- глубина погружения капилляра в жидкость, 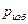 - давление Лапласа. Разность давлений воздуха в капилляре и сосуде В равна:
- давление Лапласа. Разность давлений воздуха в капилляре и сосуде В равна: .
. увеличивается, радиус кривизны мениска убывает, а кривизна возрастает. Наступает момент, когда радиус кривизны становится равным внутреннему радиусу капилляра (рис. 3в), а разность давлений
увеличивается, радиус кривизны мениска убывает, а кривизна возрастает. Наступает момент, когда радиус кривизны становится равным внутреннему радиусу капилляра (рис. 3в), а разность давлений  , (1)
, (1) - внутренний радиус капилляра. Эту разность можно определить с помощью микроманометра, так как
- внутренний радиус капилляра. Эту разность можно определить с помощью микроманометра, так как , (2)
, (2)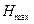 - максимальное смещение уровня жидкости в наклонной трубке микроманометра,
- максимальное смещение уровня жидкости в наклонной трубке микроманометра,  . (3)
. (3) , то ею можно пренебречь, тогда:
, то ею можно пренебречь, тогда: или
или  , (4)
, (4)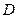 - внутренний диаметр капилляра.
- внутренний диаметр капилляра. = 103 кг/м3).
= 103 кг/м3).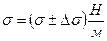 ,
, ,
,  ,
,  и
и  .
. .
. ,
, ,
, , зависящий от материала проводника, называют удельным сопротивлением. В СИ сопротивление измеряется в омах. 1 Ом - это сопротивление проводника, ток в котором равен 1 ампер, если на концах его поддерживается разность потенциалов 1 вольт:
, зависящий от материала проводника, называют удельным сопротивлением. В СИ сопротивление измеряется в омах. 1 Ом - это сопротивление проводника, ток в котором равен 1 ампер, если на концах его поддерживается разность потенциалов 1 вольт: ,
, ,
,  , I 1 =I 2 = …..= I i =In.
, I 1 =I 2 = …..= I i =In. ,
, 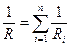 , U 1 = U 2 = ……= U i = Un.
, U 1 = U 2 = ……= U i = Un. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Мостовая схема для измерения сопротивлений приведена на рис. 1. Измерительный мост образован четырьмя резисторами: сопротивления трех из них R1, R2, R3 известны, сопротивление четвертого Rx подлежит измерению. Точками А и В мост присоединен к источнику электрического тока Е, а в диагональ CD моста включен чувствительный гальванометр G (нуль - индикатор).
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. Мостовая схема для измерения сопротивлений приведена на рис. 1. Измерительный мост образован четырьмя резисторами: сопротивления трех из них R1, R2, R3 известны, сопротивление четвертого Rx подлежит измерению. Точками А и В мост присоединен к источнику электрического тока Е, а в диагональ CD моста включен чувствительный гальванометр G (нуль - индикатор). . (1)
. (1) . (2)
. (2)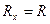 . (3)
. (3) ,
, - последовательное соединение,
- последовательное соединение, - параллельное соединение.
- параллельное соединение.
 .
. , включенной по схеме рис.2:
, включенной по схеме рис.2: .
. ,
, ,
,  .
.


