
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объясните капиллярные явления в жидкостях.Содержание книги
Поиск на нашем сайте
Если размеры сосуда, в котором находится жидкость, или, в более общем случае, если расстояние между поверхностями, ограничивающими жидкость, сравнимы с радиусом кривизны поверхности жидкости, то такие сосуды называются капиллярными. Явления, происходящие в таких сосудах, называются капиллярными явлениями. Если капилляр погрузить одним концом в жидкость, налитую в широкий сосуд, то под искривленной поверхностью в капилляре давление будет отличаться от давления под плоской поверхностью в широком сосуде на величину, определяемую формулой Лапласа: где R1 и R2 - радиусы кривизны поверхности жидкости в двух взаимно перпендикулярных сечениях. Полусумма называется средней кривизной поверхности в данной точке. Для всех форм поверхности, которые могут образоваться у жидкости, средняя кривизна остаётся постоянной для любой пары нормальных взаимно перпендикулярных сечений поверхности в данной точке. Поэтому эти сечения выбирают из соображений удобства. Для сферической поверхности R1 = R2 = R, где R – радиус сферы, поэтому для круглого капилляра формула (4) примет вид:
При смачивании стенок капилляра уровень жидкости в сферической поверхности будет выше, чем в сосуде, при несмачивании – ниже. Какие сосуды можно считать капиллярными? Чем объясняется высота поднятия жид в капилляре? Если размеры сосуда, в котором находится жидкость, или, в более общем случае, если расстояние между поверхностями, ограничивающими жидкость, сравнимы с радиусом кривизны поверхности жидкости, то такие сосуды называются капиллярными. Явления, происходящие в таких сосудах, называются капиллярными явлениями. При смачивании стенок капилляра уровень жидкости в сферической поверхности будет выше, чем в сосуде, при несмачивании – ниже. Изменение высоты уровня жидкости в узких трубках получило название капиллярности. Между жидкостью в круглом капилляре и широком сосуде устанавливается такая разность уровней h, чтобы гидростатическое давление ρgh уравновешивало капиллярное давление ∆р:
где r - плотность жидкости, a - коэффициент поверхностного натяжения на границе жидкость - газ. Радиус кривизны мениска R можно выразить через радиус капилляра r и краевой угол q. Как видно из рис.3,
Для высоты h подъёма жидкости в капилляре имеем: Высота подъема жидкости в капилляре (капиллярный подъем) растет с уменьшением радиуса капилляра и с увеличением коэффициента поверхностного натяжения жидкости. Рассказать о методе компенсации давлений в Лаб № 9. Какие давления компенсируют друг друга, и чем они вызваны? Измерение высоты столба жидкости в капилляре требует использования высокоточных приборов. Поэтому в данной работе это измерение заменяется измерением избыточного капиллярного давления Δр. Применяется метод компенсации добавочного давления. Для измерения давления используется микроманометр многопредельный с наклонной трубкой типа ММН. Если опустить в сосуд с исследуемой жидкостью капиллярную трубку, то в случае смачивания стенок трубки этой жидкостью последняя поднимается в капилляре на некоторую высоту вследствие возникновения добавочного давления (в данном случае отрицательного). Добавочное капиллярное давление для круглого капилляра в случае полного смачивания определяется формулой Dpвн=9,804×k×n получим:
|
|||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 812; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.130.154 (0.007 с.) |

 , (4)
, (4)
 . (4а)
. (4а) , (5)
, (5)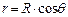 . Тогда
. Тогда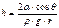 .
. .
. . Если тем или иным способом увеличить внешнее давление над поверхностью жидкости в капилляре, то можно добиться, чтобы уровни жидкости в капилляре и широком сосуде сравнялись. Очевидно, что при этом избыточное внешнее давление равно добавочному давлению, определяемому формулой
. Если тем или иным способом увеличить внешнее давление над поверхностью жидкости в капилляре, то можно добиться, чтобы уровни жидкости в капилляре и широком сосуде сравнялись. Очевидно, что при этом избыточное внешнее давление равно добавочному давлению, определяемому формулой 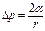 и
и .
.


