Вероят чего можно определить с помощью бин расп.

Вероят чего можно определить с помощью бин расп?

Вероятность выпадения, например, орла равна 1/2. Очевидно, необходимо провести n опытов, из которых в 50% случаев должен выпасть орел, а в 50% - решка. На практике при небольшом n это может не выполняться, то есть, например, из 10 бросаний не обязательно 5 раз выпадет орел, а 5 раз - решка. Однако в 100 опытах эта закономерность выполнится точнее, в 1000 - еще точнее и т.д. Абсолютно точно это распределение (50 х 50) выполнится при n ®¥. Однако на практике мы можем провести только конечное число опытов. В более общем случае можно определить вероятности того, что из n опытов орел выпадет 0,1,2,3,…, k,…, n раз. Примеры. Вероятность того, что из 10 подбрасываний монеты 6 раз выпадет орел, равна (p=1/2):

/Вероятность того, что из 3 бросаний игральной кости 3 раза выпадет "6", равна (p=1/6):

Вероятность рождения мальчика равна p=0,515. Вероятность того, что из 10 новорожденных будет 5 мальчиков, равна:

Что означают понятия «дискретная величина» и «непрерывная величина»?

Дискретной называется случайная величина, принимающая конечное, или счетное, число значений. Это может быть некоторый набор чисел или функция, принимающая дискретные значения. Непрерывной называется случайная величина, принимающая непрерывное множество значений. Пусть опыт по бросанию монетки повторяется n раз. Вероятность того, что из n опытов орел выпадет k раз (то есть событие А произойдет k раз), определяется биномиальным законом распределения:

где - число сочетаний из n по k, p - вероятность выпадения орла при однократном бросании (или вероятность события А), q - вероятность не выпадения орла при однократном бросании (или вероятность того, что в отдельном опыте не произойдет это событие, то есть произойдет второе событие - выпадение решки). Случайная величина k в формуле является дискретной, а результат многократных измерений некоторой физической величины a (это может быть, например, ускорение, характерный размер тела, коэффициент температуропроводности и т.д.) является непрерывной случайной величиной, так как при измерениях могут получиться любые значения внутри некоторого интервала.

Чем отличаются биномиальное распределение, распределение Лапласса-Гаусса и распределение Гаусса друг от друга?

Случайная величина k является дискретной. Дискретной называется случайная величина, принимающая конечное, или счетное, число значений. Математическое ожидание определяется следующим образом: это среднее арифметическое случайной величины, найденное с учетом вероятностей:

для биномиального распределения m_k = np. Дисперсия - это среднее квадратов отклонений случайной величины от своего математического ожидания с учетом вероятности: для биномиального s_k² = npq. Распределение Лапласа-Гаусса. При n®¥ биномиальный закон распределения вероятностей переходит в формулу Лапласа-Гаусса. Применим формулу Стирлинга. 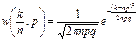- формула Лапласа-Гаусса. Это распределение совпадает с биномиальным распределением, математическое ожидание и дисперсия вычисляются по тем же формулам. Тогда Здесь случайная величина k, так же, как и в биномиальном законе, является дискретной. Распределение Гаусса: 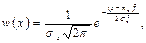где m_x - математическое ожидание x, s_x² - дисперсия x. Функция w(x) определяет вероятность того, что x лежит в интервале x, x+dx. С другой стороны, на систему действуют случайные причины, которые вызывают независимые друг от друга отклонения +s и - s, причем p(+s)+p(-s) =1. Совокупность этих отклонений вызывает ошибку D x=x-<x>. Это совпадает с моделью биноминального эксперимента, а распределение Лапласа-Гаусса, практически совпадает с законом Гаусса. Отличие в том, что в распределении Лапласа-Гаусса фигурирует дискретная случайная величина k, а в другом непрерывная случайная величина х. Математическое ожидание и дисперсия определяются: , .

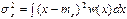Миллиметр ртутного столба

1 мм рт. см. равен гидростатическому давлению столба ртути высотой 1 мм и плотностью 13 595,1 кг/м 3 при ускорении свободного падения g = 9,80665 м/с 2.

Соотношение между мм рт. ст. и другими единицами давления:

1 мм рт. ст. = 133,322 н/м 2 = 13,5951 мм вод. ст.

1 psi = 6894,757 паскалей (или 6894,757 ньютонов на метр квадратный).

Вероят чего можно определить с помощью бин расп?

Вероятность выпадения, например, орла равна 1/2. Очевидно, необходимо провести n опытов, из которых в 50% случаев должен выпасть орел, а в 50% - решка. На практике при небольшом n это может не выполняться, то есть, например, из 10 бросаний не обязательно 5 раз выпадет орел, а 5 раз - решка. Однако в 100 опытах эта закономерность выполнится точнее, в 1000 - еще точнее и т.д. Абсолютно точно это распределение (50 х 50) выполнится при n ®¥. Однако на практике мы можем провести только конечное число опытов. В более общем случае можно определить вероятности того, что из n опытов орел выпадет 0,1,2,3,…, k,…, n раз. Примеры. Вероятность того, что из 10 подбрасываний монеты 6 раз выпадет орел, равна (p=1/2):

/Вероятность того, что из 3 бросаний игральной кости 3 раза выпадет "6", равна (p=1/6):

Вероятность рождения мальчика равна p=0,515. Вероятность того, что из 10 новорожденных будет 5 мальчиков, равна: