
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое моделирование связи методом корреляционного и регрессионного анализаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В общем виде задача статистики в области изучения взаимосвязей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых, должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на результативный признак. Задачами регрессионного анализа являются выбор типа модели (формы связи), установление степени влияния независимых переменны на зависимую и определение расчетных значений, зависимой переменной (функции регрессии). Решение всех названных задач приводит к необходимости комплексного использования этих методов. Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле модель — это аналог, условный образ (изображение, описание, схема, чертеж и т.п.) какого-либо объекта, процесса или события, приближенно воссоздающий "оригинал". Модель представляет собой логическое или математическое описание компонентов и функций, отображающих существенные свойства моделируемого объекта или процесса, дает возможность установить основные закономерности изменения оригинала. В модели оперируют показателями, исчисленными для качественно однородных массовых явлений (совокупностей). Выражение модели в виде функциональных уравнений используют для расчета средних значений моделируемого показателя по набору заданных величин и для выявления степени влияния на него отдельных факторов. По количеству включаемых факторов модели могут быть однофакторными и многофакторными (два и более факторов). В зависимости от познавательной цели статистические модели подразделяются на структурные, динамические и модели связи. Рассмотрим основные проблемы статистического моделирования связи методами корреляционного и регрессионного анализа. Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный линейный корреляционный и регрессионный анализ). Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака* на результативный признаку и представляющая собой однофакторный корреляционный и регрессионный анализ. Овладение теорией и практикой построения и анализа двухмерной модели корреляционного и регрессионного анализа представляет собой исходную основу для изучения многофакторных стохастических связей. Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться эмпирически — перебором и оценкой функций разных типов и т.п. При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) регрессии имеет вид:
где Поскольку a0 является средним значением у в точке х = 0, экономическая интерпретация часто затруднена или вообще невозможна. Коэффициент парной линейной регрессии а1 имеет смысл показателя силы связи между вариацией факторного признака x и вариацией результативного признака у. Уравнение (5.3) показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у. приходящуюся на единицу вариации х. Знак а1 указывает направление этого изменения. Параметры уравнения а0, a1 находят методом наименьших квадратов (метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), т.е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi от выровненных
Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
Решим эту систему в общем виде:
Определив значения
Проверка адекватности регрессионной модели. Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии и корреляции — параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько зги показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей. При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n < 30) осуществляют с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t-критерия для параметра a0
для параметра a1
где n- объем выборки
(5.10) – среднее квадратическое отклонение результативного признака у от выравненных значений
Или
-среднеквадратическое отклонение факторного признака х от общей средней Вычисленные значения, сравнивают с критическими t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости а и числом степеней свободы вариации v=n-2. В социально-экономических исследованиях уровень значимости а обычно принимают равным 0,05. Параметр признается значимым (существенным) при условии, если tрасч.>tтабл. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями. Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у. Теснота корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением
где
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отлипать от эмпирического корреляционного отношения — теоретическое. Теоретическое корреляционное отношение η представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значений результативного признака
где
Тогда результативного признака.
Изменение значения η объясняется влиянием факторного признака. В основе расчета корреляционного отношения лежит правило сложения дисперсий, т.е.
где
Тогда формула теоретического корреляционного отношения примет вид:
или Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации (меры определенности, причинности). Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака-фактора. Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком. При криволинейных связях теоретическое корреляционное отношение, исчисляемое по вышеприведенным формулам часто называют индексом корреляции R. Как видно из приведенных формул, корреляционное отношение может находиться в пределах от 0 до 1, т.е. (0<η<1). Чем ближе корреляционное отношение к 1, тем связь между признаками теснее. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи — линейный коэффициент корреляции:
Или Для практических вычислений при малом числе наблюдений n≤20÷30 линейный коэффициент корреляции исчисляют по формуле:
Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -1 < г < 1. Отрицательные значения указывают на обратную связь, Квадрат линейного коэффициента корреляции г2 называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено и пределах от 0 до 1, т.е. 0 ≤ г2 ≤1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции. Факт совпадений и несовпадений значений теоретического корреляционного отношения η и линейного коэффициента корреляции г используется для оценки формы связи. Выше отмечалось, что посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции — только прямолинейной. Следовательно, значения η и г2 совпадают только при наличии прямолинейной связи. Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что если разность квадратов η2 и г2 не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной. Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность. Для оценки значимости коэффициента корреляции г используют t-критерий Стьюдента, который применяется при t- распределении, отличном от нормального. При линейной однофакторной связи t-критерий можно рассчитать по формуле:
где (n-2) — число степеней свободы при заданном уровне значимости α, и объеме выборки n. Полученное значение Экономическая интерпретация параметров регрессии. После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака -фактора на результативный признак (показатель). Для удобства интерпретации параметра а1 используют коэффициент эластичности. Он показывает средние изменения результативного признака при изменении факторного признака на 1 % и вычисляется по формуле, %:
Непараметрические методы Применение корреляционного и регрессионного анализа требует, чтобы все признаки были количественно измеренными. Построение аналитических группировок предполагает, что количественным должен быть результативный признак. Параметрические методы основаны на использовании основных количественных параметров распределения (средних величин и дисперсий). Вместе с тем в статистике применяются также непараметрические методы, с помощью которых устанавливается связь между качественными (атрибутивными) признаками. Сфера их применения шире, чем параметрических, поскольку не требуется соблюдения условия нормальности распределения зависимой переменной, однако при этом снижается глубина исследования связей. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерении ее тесноты. В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками, представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициенты ассоциации и контингенции. Коэффициент ассоциации определяется по формуле
Коэффициент контингенции определяется по формуле
где a, b,c,d - частоты (число единиц). Для расчета коэффициентов ассоциации и контингенции строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений признака.
Коэффициенты ассоциации и контингенции изменяются от —1 до +1; чем ближе к +1 или -1, тем сильнее связаны между собой изучаемые признаки. Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной,если К,>0,5 или К,>0,3. Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателей взаимной сопряженности Пирсона.
где Вычтя из этой суммы единицу, получим Вспомогательная таблица для расчета коэффициентов взаимной сопряженности из трех групп имеет следующий вид:
Коэффициенты взаимной сопряженности Пирсона и Чупрова изменяются от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков. В анализе социально - экономических явлений часто приходится прибегать к различным условным оценкам, например рангам, а взаимосвязь между признаками измерять с помощью непараметрических коэффициентов связи. Данные коэффициенты исчисляются при условии, что исследуемые признаки подчиняются различным законам распределения. Ранжирование - это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения. Ранг - это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые определяют. Такие ранги называются связанными К непараметрическим ранговым коэффициентам связи можно отнести коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов Спирмена, ранговый коэффициент корреляции Кендалла, Коэффициент корреляции знаков Фехнера основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков, а не на сопоставлении попарно размеров отклонений индивидуальных значений факторного и результативного признаков от средней. Формула коэффициента корреляции знаков Фехнера
где а число пар с одинаковыми знаками отклонений х и у от Коэффициент Фехнера колеблется в пределах от -1 до +1. Чем ближе коэффициент к 1, тем теснее связь. Если Коэффициент корреляции рангов Спирмена исчисляется не по первичным данным, а по рангам (порядковым номерам),которые присваиваются всем значениям изучаемых признаков, расположенным в порядке предпочтительности. Если значения признаков совпадают, то определяется средний ранг. Коэффициент корреляции рангов Спирмена определяется по формуле:
где число рангов; Коэффициент корреляции рангов также колеблется от -1 до + 1. Если ранги по обеим признакам совпадают, то Коэффициент корреляции рангов Кендалла может также использоваться для измерения взаимосвязи между качественными и количественными признаками, ранжированными по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле;
где n-число наблюдений; S-сумма, включающая два слагаемых Р и Q, т.е. S=P+Q. Для нахождения Р нужно установить, сколько чисел, находящихся после каждого из элементов последовательности рангов переменной у, имеют величину ранга, превышающую ранг рассматриваемого элемента. Суммируя эти числа получают значение Р, которое можно рассматривать как меру соответствия последовательности рангов переменной у последовательности переменной х. Второе слагаемое Q характеризует степень несоответствия последовательности рангов переменной у последовательности рангов переменной х. Чтобы подсчитать Q определяют сколько чисел после каждого из членов последовательности рангов переменной у имеет ранг меньше, чем у рассматриваемого. Такие величины берутся со знаком минус. Коэффициент корреляции рангов Кендалла основан на сравнении общего итога суммы положительных и отрицательных баллов (S=P=Q) с максимальным значением одного из слагаемых. Коэффициент Кендалла также изменяется от -1 до +1 и равен кулю при отсутствия связи.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 856; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.68.161 (0.009 с.) |

 (1.7.3.)
(1.7.3.) -теоретические значения результативного признака, полученные по уравнению регрессии; а0, a1 — коэффициенты (параметры) уравнения регрессии.
-теоретические значения результативного признака, полученные по уравнению регрессии; а0, a1 — коэффициенты (параметры) уравнения регрессии. :
: (1.7.4.)
(1.7.4.) (1.7.5.)
(1.7.5.)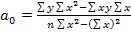 (1.7.6.)
(1.7.6.) (1.7.7.)
(1.7.7.)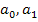 и подставив их в уравнение связи
и подставив их в уравнение связи находим значения
находим значения  х , зависящие только от заданного значения х.
х , зависящие только от заданного значения х. (1.7.8.)
(1.7.8.) (1.7.9.)
(1.7.9.) (1.7.10.)
(1.7.10.)
 (1.7.11.)
(1.7.11.) (1.7.12.)
(1.7.12.) .
.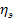 , когда
, когда  (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней:
(межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней: (1.7.13.)
(1.7.13.) - общая дисперсия результативного признака.
- общая дисперсия результативного признака. (1.7.14.)
(1.7.14.) (1.7.15.)
(1.7.15.) т.е. рассчитанных по уравнению регрессии, со средним квадратаческим отношением эмпирических (фактических) значений результативности признака
т.е. рассчитанных по уравнению регрессии, со средним квадратаческим отношением эмпирических (фактических) значений результативности признака  :
: (1.7.16.)
(1.7.16.) - дисперсия выровненных значений результативного признака
- дисперсия выровненных значений результативного признака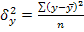 (1.7.18.)
(1.7.18.) (1.7.19.)
(1.7.19.) (1.7.20.)
(1.7.20.) - отражает вариацию у за счет всех остальных факторов, кроме X, т.е. является остаточной дисперсией:
- отражает вариацию у за счет всех остальных факторов, кроме X, т.е. является остаточной дисперсией: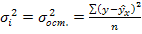 (1.7.21.)
(1.7.21.) (1.7.22)
(1.7.22) (1.7.23.)
(1.7.23.) (1.7.24.)
(1.7.24.) (1.7.25.)
(1.7.25.) (1.7.26.)
(1.7.26.)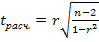 (1.7.27.)
(1.7.27.) сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение
сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение  то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т.е. отклоняется гипотеза о его случайности).
то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т.е. отклоняется гипотеза о его случайности). (1.7.28.)
(1.7.28.) (1.7.29.)
(1.7.29.) (1.7.30.)
(1.7.30.) у
х
у
х
 , где
, где 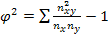 ,а
,а  или
или и Чупрова.
и Чупрова. (1.7.31.)
(1.7.31.) — число возможных значений первой статистической величины (число групп по столбцам);
— число возможных значений первой статистической величины (число групп по столбцам);  - число возможных значений второй статистической величины (число групп по строкам);
- число возможных значений второй статистической величины (число групп по строкам);  - показатель взаимной сопряженности (определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки).
- показатель взаимной сопряженности (определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки). .
. (1.7.32.)
(1.7.32.) и
и  ;
;  -число пар с разными знаками отклонений х и у от
-число пар с разными знаками отклонений х и у от >0 связь прямая, если
>0 связь прямая, если 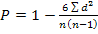 (1.7.33.)
(1.7.33.) - квадрат разности рангов для каждой единицы, d = Rx — Ry; n-
- квадрат разности рангов для каждой единицы, d = Rx — Ry; n- 0, значит р=1 и связь полная прямая. Бели р=-1, то связь полная обратная. При р=0 связь отсутствует.
0, значит р=1 и связь полная прямая. Бели р=-1, то связь полная обратная. При р=0 связь отсутствует. (1.7.34.)
(1.7.34.)


