
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы выявления корреляционной связиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выделяют три этапа изучения связей между явлениями. В основе первого этапа лежит качественный анализ состава явления методами экономики, социологии и других наук. Второй этап предполагает построение модели связи с помощью методов группировки, средних величин, индексного метода и др. Третий этап состоит в интерпретации результатов в соответствии с качественными особенностями изучаемого явления. При исследовании корреляционных связей между признаками необходимо решить следующие задачи: § предварительно проанализировать свойства изучаемой совокупности; § установить факт наличия связи, определить ее направление и формы; § измерить степень тесноты связи между признаками; § построить регрессионную модель (найти аналитическое выражение связи); § оценить адекватность модели, возможность ее экономической интерпретации и практического использования. Таким образом, статистика не только определяет наличие взаимосвязей социально-экономических явлений, но и дает количественную характеристику этих взаимосвязей. Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: метод параллельных рядов; графический; метод аналитических группировок; дисперсионный анализ; корреляционно-регрессионный анализ. Метод параллельных рядов состоит в том, чтостатистические показатели располагают в виде параллельных рядов – ряда значений факторного признака Графический метод позволяет наглядно судить о наличии, направлении и форме связи с помощью графика поля корреляции. На оси абсцисс откладываются значения факторного признака, а на оси ординат – результативного. На графике откладываются все единицы, имеющие значения
Рис. 10.1. График поля корреляции
На рис. 10.1 видно, что эмпирическая линия связи при некотором приближении имеет вид прямой линии. Поэтому можно предположить наличие прямолинейной корреляционной связи между признаками. Если значения результативного признака изменяются неравномерно, то эмпирическая линия связи будет приближаться к некоторой кривой. В этом случае можно предположить наличие криволинейной (нелинейной) корреляционной связи (рис. 10.2).
Рис. 10.2. Вид криволинейной обратной связи Метод аналитических группировок состоит в том, что единицы совокупности группируются, как правило, по факторному признаку. Для каждой группы по результативному признаку рассчитывается средняя или относительная величина. Для выявления характера связи между признаками сопоставляют изменения значений (средних или относительных) результативного признака с изменениями значений факторного признака. Метод дисперсионного анализа позволяетрешить две задачи: 1) определить долю систематической и случайной вариаций в общей вариации; 2) установить роль факторного признака в изменении результативного признака. Замечание. Дисперсионный анализ – это раздел математической статистики, изучающий степень влияния одного или нескольких факторных признаков на результативный признак при небольшом числе наблюдений. Отличие дисперсионного анализа от корреляционного состоит в том, что измерение колеблемости в дисперсионном анализе осуществляется на основе расчета дисперсий. В дисперсионном анализе используются одно- и многофакторные статистические комплексы, т.е. комбинационные таблицы, в которых определена (представлена) структура качественно разнородной статистической совокупности. Таким образом, дисперсионный анализ применяют для установления существенности влияния качественных факторов на исследуемую величину. Метод корреляционно-регрессионного анализа позволяет оценить тесноту и направление связи, получить уравнение зависимости между факторными и результативными признаками.
Статистическое изучение социально-экономических явлений предполагает не только выявление связи между признаками, но и построение математической модели (аналитическое выражение) этой связи. Уравнение парной регрессии
При статистическом изучении корреляционных зависимостей решаются две основные задачи: 1) нахождение формы связи между признаками 2) измерение тесноты связи. Эти задачи являются неразрывными и взаимно дополняющими друг друга задачами корреляционно-регрессионного анализа. Решение данных задач допускается в разной последовательности. В настоящем пособии сначала рассматривается нахождение уравнения регрессии, а затем – методы выявления и измерения тесноты связи. Определение формы связи называется нахождением уравнения регрессии (уравнения связи). Регрессия – это зависимость среднего значения случайной величины от одной или нескольких величин. Термин «регрессия» (от лат. regression – отступление, возврат к чему-либо) введен Ф. Гальтоном в 1886 г. Парная регрессия позволяет получить аналитическое выражение связи между двумя признаками: факторным Найти уравнение регрессии – значит по фактическим (эмпирическим) данным математически описать изменения взаимно коррелируемых величин. Уравнение регрессии также называют теоретической линией регрессии – это линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление (основную тенденцию) связи. Теоретическая линия регрессии позволяет оценить среднее значение результативного признака Значения результативного признака, рассчитанные по уравнению регрессии, называются теоретическими Аналитическая связь между признаками может описываться следующими уравнениями: § прямая: § парабола: § гипербола: Считается, что если факторный и результативный признаки изменяются одинаково (примерно в арифметической прогрессии), то это свидетельствует о линейной связи между ними. Если признаки изменяются в разных направлениях, то связь является обратной. В этом случае применяется уравнение гиперболы. А если признаки изменяются в одном направлении, но с разной скоростью, то применяется параболическая или степенная функция. После выбора типа функции определяют параметры уравнения регрессии. Параметры должны быть такими, чтобы рассчитанные с их помощью теоретические значения результативного признака Уравнение парной линейной регрессии имеет вид:
где:
Знак при коэффициенте регрессии показывает направление связи между признаками: § при § при Параметры уравнения регрессии (
Рассмотрим парную линейную регрессию, так как линейная зависимость является наиболее используемой формой связи между двумя признаками. Найдя частные производные указанной суммы по
где Решение этой системы дает параметры уравнения регрессии. Для нахождения параметров
Однако значения параметров
Теперь, зная значение Если связь выражена параболой, то для отыскания параметров уравнения
Решив систему, получим уравнение регрессии вида:
Оценка обратной зависимости признаков
Также коэффициент регрессии
Коэффициент регрессии применяется для определения коэффициента эластичности Коэффициент эластичности определяется по формуле:
Для большинства форм связи коэффициент эластичности является переменной величиной, т.е. изменяется в соответствии с изменением значений фактора
|
|||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 724; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.94.93 (0.01 с.) |

 и соответствующих ему значений результативного признака
и соответствующих ему значений результативного признака 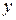 . При этом значения факторного признака располагают по возрастанию. С этими значениями сопоставляются изменения значений результативного признака. Такое сопоставление рядов позволяет установить характер и тесноту связи. Если значения признаков
. При этом значения факторного признака располагают по возрастанию. С этими значениями сопоставляются изменения значений результативного признака. Такое сопоставление рядов позволяет установить характер и тесноту связи. Если значения признаков 


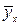 . То есть, теоретические значения рассматриваются в виде функции, т.е.
. То есть, теоретические значения рассматриваются в виде функции, т.е. 
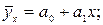

 и др.
и др. ).
).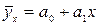 ,
, - свободный член уравнения (не имеет экономического смысла);
- свободный член уравнения (не имеет экономического смысла);  - коэффициент регрессии, который показывает, на сколько единиц в среднем изменится результативный признак при изменении факторного признака на единицу его измерения. При такой интерпретации коэффициента регрессии
- коэффициент регрессии, который показывает, на сколько единиц в среднем изменится результативный признак при изменении факторного признака на единицу его измерения. При такой интерпретации коэффициента регрессии  .
.
 - объем исследуемой совокупности.
- объем исследуемой совокупности.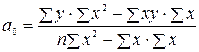 ;
;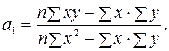
 .
.
 применяется система нормальных уравнений вида:
применяется система нормальных уравнений вида: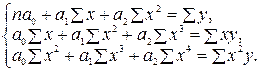

 по формуле:
по формуле: .
. , который показывает, на сколько процентов изменится в среднем величина результативного признака
, который показывает, на сколько процентов изменится в среднем величина результативного признака 



