
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вариация альтернативного признакаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Наряду с вариацией количественного признака в статистике может ставиться задача оценки вариации качественного признака. При наличии двух взаимоисключающих вариантов значений признака говорят о наличии альтернативной изменчивости качественного признака. В таких случаях возникает необходимость в измерении дисперсии альтернативных признаков, т.е. признаков, которыми обладают одни единицы и не обладают другие. Введем обозначения: 1 - наличие данного признака; 0 – отсутствие признака; р =
Тогда справедливо равенство Среднее значение альтернативного признака:
Дисперсия альтернативного признака определяется по формуле:
Среднее квадратическое отклонение альтернативного признака: Предельное значение вариации альтернативного признака равно 0,25; оно получается при Правило сложения дисперсий Изучая дисперсию признака в совокупности и проводя расчеты помощью общей средней, нельзя оценить влияние отдельных факторов на колеблемость индивидуальных значений признака. Это можно сделать с помощью метода группировок: единицы изучаемой совокупности подразделяются на однородные группы по признаку-фактору. В случае разделения совокупности на группы по какому-либо признаку существует возможность оценки влияния этого признака-фактора на колеблемость индивидуальных значений. Наряду с изучением вариации признака по совокупности в целом, появляется возможность проследить количественные изменения признака: 1) по группам, на которые разделяется совокупность; 2) а также между группами. При этом кроме общей средней для всей совокупности исчисляются: - средние по отдельным группам (групповые или частные средние); - три показателя дисперсии: • общая дисперсия • межгрупповая дисперсия • средняя внутригрупповая дисперсия Общая дисперсия
где: Межгрупповая дисперсия
где:
Средняя внутригрупповая дисперсия
где Средняя внутригрупповая дисперсия Между указанными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий: величина общей дисперсии равна сумме межгрупповой и средней внутригрупповой дисперсии:
Это правило показывает, что общая вариация признака в совокупности складывается из вариации признака внутри отдельных групп и вариации между ними. Разные виды дисперсий широко используют для исчисления показателей тесноты связи между признаками. Показателями тесноты связи служат эмпирическое корреляционное отношение и коэффициент детерминации. В частотности, на основании правила сложения дисперсии рассчитывается эмпирическое корреляционное отношение
Эмпирическое корреляционное отношение может быть только положительным. Качественная интерпретация показателя связи Таблица 6.3
|
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1060; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.007 с.) |

 - доля единиц, обладающих данным признаком;
- доля единиц, обладающих данным признаком;  число единиц совокупности, обладающие данным признаком; n- число наблюдений.
число единиц совокупности, обладающие данным признаком; n- число наблюдений.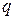 - доля единиц, не обладающих данным признаком;
- доля единиц, не обладающих данным признаком; ,
, 




 ;
;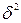 ;
; .
. ,
, - общая средняя арифметическая для всей совокупности;
- общая средняя арифметическая для всей совокупности; вокруг общей средней
вокруг общей средней  ,
, - число единиц в отдельной группе;
- число единиц в отдельной группе;
 ,
, - внутригрупповая дисперсия отдельной группы, дает оценку колеблемости признака внутри каждой
- внутригрупповая дисперсия отдельной группы, дает оценку колеблемости признака внутри каждой  ой группы.
ой группы.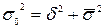 .
. («эта»). Этот показатель позволяет определить тесноту связи между факторным (группировочным) и результативным признаками. Он определяется по формуле:
(«эта»). Этот показатель позволяет определить тесноту связи между факторным (группировочным) и результативным признаками. Он определяется по формуле: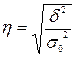 ,
, 



