
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели тесноты связи между количественными признакамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистическое изучение взаимосвязей социально-экономических явлений предполагает измерение тесноты (силы) и направления связи. Нахождение уравнения регрессии сопровождается измерением тесноты связи между признаками. Связь между количественными признаками измеряется через их вариацию. При измерении тесноты корреляционной связи ставится задача – определить, в какой мере вариация результативного признака вызвана вариацией факторного признака. Теснота связи между количественными признаками измеряется с помощью следующих показателей: § линейный коэффициент корреляции § эмпирическое § коэффициент Фехнера § ранговые коэффициенты связи Спирмена § коэффициент конкордации Линейный коэффициент корреляции При расчете коэффициента учитывается величина отклонений признаков от средних значений:
После преобразования данной формулы можно получить следующее выражение для расчета линейного коэффициента корреляции:
В статистике используются различные модификации формулы расчета данного коэффициента:
где
Линейный коэффициент корреляции может принимать значения от -1 до +1: Интерпретация значений коэффициента корреляции представлена в табл. 10.2. Таблица 10.2 Оценка линейного коэффициента корреляции
Таким образом, линейный коэффициент парной корреляции одновременно характеризует тесноту и направление связи. Коэффициент корреляции является симметричной мерой связи между признаками Рассмотрим порядок проверки коэффициента корреляции на значимость (существенность).
Коэффициент корреляции является выборочным показателем, поэтому он может содержать случайную ошибку, и не всегда однозначно отражать реальную связь между изучаемыми показателями. Поэтому, чтобы оценить существенность (значимость) самого коэффициента и реальность измеряемой связи, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции Для оценки существенности (значимости) линейного коэффициента корреляции необходимо сопоставить его со средней квадратической ошибкой:
Если число наблюдений
Значимость линейного коэффициента корреляции проверяется на основе
При этом выдвигается и проверяется нулевая гипотеза Если нулевая гипотеза верна, т.е.
По таблице распределения Стьюдента (Приложение 5) находится критическое значение tтабл., которое допустимо при справедливости нулевой гипотезы. С этим значением сравнивается фактическое (расчетное) значение tрасч.. При этом, если Если Величина С помощью линейного коэффициента связи Таблица 10.3
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.152 (0.011 с.) |

 ;
; и теоретическое корреляционное отношение
и теоретическое корреляционное отношение  ;
; ;
; и Кендалла
и Кендалла  ;
; .
. .
. .
. ;
; ,
, - коэффициент регрессии в уравнении связи;
- коэффициент регрессии в уравнении связи; - среднее квадратическое отклонение соответствующего факторного признака. Знаки коэффициентов регрессии и корреляции совпадают.
- среднее квадратическое отклонение соответствующего факторного признака. Знаки коэффициентов регрессии и корреляции совпадают. . Знак «-» означает, что связь обратная, а знак «+» свидетельствует о наличии прямой связи.
. Знак «-» означает, что связь обратная, а знак «+» свидетельствует о наличии прямой связи.

 уменьшается
уменьшается 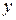 ,
и наоборот
,
и наоборот




 .
. .
. 30, то средняя ошибка линейного коэффициента корреляции определяется по формуле:
30, то средняя ошибка линейного коэффициента корреляции определяется по формуле: .
. - критерия Стьюдента:
- критерия Стьюдента: .
. :
:  о равенстве коэффициента корреляции нулю (гипотеза об отсутствии связи между х и у в генеральной совокупности)
о равенстве коэффициента корреляции нулю (гипотеза об отсутствии связи между х и у в генеральной совокупности) (обычно принимается за 0,05) и числом степеней свободы
(обычно принимается за 0,05) и числом степеней свободы 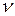 = п -2.
= п -2. >
>  , то нулевая гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции. Следовательно, связь между х и у является статистически существенной (реальной).
, то нулевая гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции. Следовательно, связь между х и у является статистически существенной (реальной). получено случайно), связь между х и у отсутствует.
получено случайно), связь между х и у отсутствует. носит название коэффициента детерминации. Он показывает, в какой степени результативный признак зависит от факторного признака. Очевидно, что чем ближе коэффициент к 100 %, тем теснее выявленная зависимость между признаками.
носит название коэффициента детерминации. Он показывает, в какой степени результативный признак зависит от факторного признака. Очевидно, что чем ближе коэффициент к 100 %, тем теснее выявленная зависимость между признаками.


