
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды, методы и способы отбораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Выборочная совокупность будет полно и адекватно отражать свойства генеральной совокупности в том случае, если она будет репрезентативной (представительной). Репрезентативность выборки зависит от применяемых видов, методов и способов отбора единиц. Достоверность результатов наблюдения достигается за счет соблюдения основного принципа выборочного наблюдения: обеспечение случайности отбора единиц (равная возможность единиц попасть в выборку) В теории выборочного наблюдения разработаны различные виды, методы и способы отбора единиц из генеральной совокупности. Различают два вида отбора единиц в выборочную совокупность: повторный и бесповторный. При повторном отборе отобранная единица подвергается обследованию, возвращается в генеральную совокупность и снова может быть выбранной («схема возвратного шара»). В результате вероятность попадания отдельной единицы в выборку не меняется независимо от числа отобранных единиц. На практике такой отбор применяется, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями регистрируемых признаков (например, в маркетинговых исследованиях). В социально-экономических исследованиях повторный отбор встречается редко. При бесповторном отборе отобранная единица подвергается обследованию и в дальнейшей процедуре отбора не участвует («схема безвозвратного шара»). Тем самым, вероятность попасть в выборку для оставшихся единиц увеличивается с каждым шагом отбора. Такой вид отбора практически возможен, когда объем генеральной совокупности четко определен.
В ходе выборочного наблюдения могут применяться следующие способы отбора единиц из генеральной совокупности: § индивидуальный отбор - в выборку отбираются отдельные единицы совокупности; § групповой отбор - в выборку попадают качественно однородные группы или серии единиц; § комбинированный отбор – сочетание индивидуального и группового способов отбора. Выборочная совокупность может быть сформирована с помощью следующих методов отбора единиц: 1. случайный (собственно-случайный); 2. механический; 3. типический (расслоенный, стратифицированный); 4. серийный (гнездовой); 5. комбинированный. Приведем краткую характеристику этих методов отбора единиц. Собственно-случайный (случайный) отбор – индивидуальный отбор единиц, каждой из которых присвоен порядковый номер, с помощью жеребьевки или таблицы случайных чисел (Приложение 3). Генеральная совокупность предварительно не разделяется на какие-либо группы. Условием репрезентативности выборки служит принцип случайности (равная возможность каждой единицы попасть в выборку). Собственно-случайная выборка может осуществляться по схемам повторного и бесповторного обора (например, проведение тиражей денежно-вещевой лотереи). Механический отбор – отбор из предварительно упорядоченной и разбитой на равные интервалы (группы) генеральной совокупности. Размер интервала равен обратной величине доли выборки. Например, при 5 % - ной выборке отбирается каждая 20-я единица (1/0,05), при 10 %-ной выборке - каждая 10-я единица (1/0,1) и т.д. В результате, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица. При этом отбор начинается не с первой единицы совокупности, а с середины первого интервала. Для обеспечения репрезентативности все единицы генеральной совокупности должны располагаться в определенном порядке. Механический отбор всегда бывает бесповторным. Он имеет преимущество перед случайным отбором, т.к. его легче организовать. Типический отбор(расслоенный, стратифицированный) – неоднородная генеральная совокупность вначале разбивается на качественно однородные типические группы (не обязательно равные). Затем из каждой группы производится индивидуальный отбор случайным или механическим методом. Типическая выборка применяется при изучении сложных статистических совокупностей и дает более точные результаты по сравнению с другими методами отбора. В частности, случайная ошибка при типическом отборе меньше, чем при собственно-случайном и механическом отборе. Это объясняется тем, что имевшееся соотношение между группами единиц генеральной совокупности, сохраняется и в выборочной совокупности. Типический отбор бывает повторным и бесповторным. Из каждой типической группы в выборочную совокупность можно отбирать определенное число единиц с помощью следующих разновидностей типического отбора: 1. пропорциональный типический отбор – число единиц выборки n пропорционально удельному весу каждой группы в генеральной совокупности: где:
2. непропорциональный типический отбор - число единиц выборки непропорционально удельному весу каждой группы в генеральной совокупности:
где 3. отбор с учетом вариации признака -число единиц выборки пропорционально удельному весу в генеральной совокупности с учетом вариации признака по группам: - для средней - для доли Серийный (гнездовой)отбор – это отбор, при котором в случайном порядке отбираются не отдельные единицы, а целые группы единиц (серии, гнезда), которые подвергаются сплошному наблюдению. Отбор отдельных серий осуществляется на основе случайного или механического метода. Серийный отбор применяется в том случае, если генеральная совокупность разбита на группы еще до начала выборочного наблюдения. На практике чаще применяется бесповторный отбор с равными сериями. Ошибка серийной выборки больше, чем при другом методе отбора. Но серийный отбор обладает организационными преимуществами, поэтому довольно часто применяется на практике. Серийную выборку применяют в двух случаях: 1) все серии имеют одинаковое количество единиц; 2) серии различны по объему. Серийный отбор обеспечивает экономию средств, если обследования распространяются на обширную территорию и гнездами являются территориальные единицы. В рассмотренных выше методах осуществлялся одноступенчатый и многоступенчатый отбор единиц в выборочную совокупность. При одноступенчатой выборке каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайный и серийный отбор). При многоступенчатой выборке применяется несколько стадий (ступеней) отбора. Производят отбор отдельных групп из генеральной совокупности, затем из групп выбираются отдельные единицы (механический отбор). При этом каждая стадия имеет свою единицу отбора. Число ступеней определяется числом типов единиц отбора. Например, на последней ступени единица отбора совпадает с единицей выборки. Ошибка всей выборки складывается из ошибок на отдельных ступенях отбора. При построении многоступенчатой выборки используется комбинация разных методов отбора, поэтому такой метод отбора иногда называют комбинированной выборкой. От многоступенчатого отбора следует отличать многофазный отбор. В отличие от многоступенчатого отбора, он предполагает сохранение одной и той же единицы отбора на всех этапах его проведения. При этом отобранные на каждой стадии единицы подвергаются обследованию по более широкой программе. Многофазная выборка используется для расширения программы обследования. Особым видом выборочного наблюдения явления моментное наблюдение, т.е. выборочное наблюдение во времени. При этом все единицы изучаемой совокупности подлежат сплошному учету: объектами выборки служат отрезки времени. Поэтому понятия генеральной и выборочной совокупности относятся не к совокупности единиц, а ко времени наблюдения. Ошибки выборки Выборочное наблюдение носит несплошной характер, поэтому оно сопровождается ошибками (погрешностями). Ошибки выборочного наблюдения возникают в двух случаях: 1. при сборе данных (ошибки регистрации); 2. в результате неполного учета единиц генеральной совокупности (ошибки репрезентативности). Таким образом, любому выборочному наблюдению свойственна ошибка репрезентативности - расхождение между характеристиками выборочной и генеральной совокупности (рис 7.1).
Рис 7.1. Виды ошибок репрезентативности Ошибка репрезентативности возникает в результате того, что выборочная совокупность не полностью отражает закономерности, присущие генеральной совокупности. Величина случайной ошибки репрезентативности зависит: 1) от объема выборки; 2) от степени вариации признака в генеральной совокупности; 3) от метода отбора единиц и т.д. По данным выборочной совокупности оценивают показатели (параметры) генеральной совокупности. Например, используют оценку 2-х параметров: - генеральной средней величины изучаемого признака (для количественного признака); - генеральной доли (для альтернативного признака). Теоретическое обоснование появления случайных ошибок выборки объясняют предельные теоремы теории вероятностей. Так как случайная ошибка выборки возникает в результате случайных различий между границами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки эта ошибка будет сколь угодно мала. Поэтому характеристики выборки могут достаточно хорошо представлять характеристики генеральной совокупности. Случайные ошибки могут быть доведены до незначительных размеров, что позволит определить их размеры и пределы с достаточной степенью точности на основании закона больших чисел. Выборочное распределение средней величины будет приближаться к нормальному распределению по мере увеличения объема выборки Одной из задач выборочного метода является определение ошибок выборки, т.е. возможных расхождений характеристик совокупностей: 1) между выборочной средней ( 2) между выборочной долей единиц Методы математической статистики позволяют измерить эти ошибки и указать границы их колеблемости. Величину ошибок можно оценить по формулам:
В статистике различают три вида ошибок выборки: - средняя ошибка - предельная ошибка - относительная ошибка Вид формулы средней ошибки выборки зависит от метода отбора. Рассмотрим порядок расчета ошибок выборки при собственно-случайном отборе. Средняя ошибка выборки Рассмотрим формулы средней ошибки выборки 1. При повторном отборе: 1.1. Средняя ошибка выборочной средней
1.2. Средняя ошибка выборочной доли
2. При бесповторном отборе: 2.1. Средняя ошибка выборочной средней
2.2. Средняя ошибка выборочной доли
где
Замечание. На практике величина дисперсии признака в генеральной совокупности
При большой численности выборочной совокупности Замечание. Поскольку при бесповторном отборе в ходе выборки объем генеральной совокупности Средняя ошибка выборки при собственно-случайном повторном отборе зависит от: - объема выборки - степени вариации признака (прямая зависимость). Чем больше вариация признака, тем больше ошибка выборки. Для ее уменьшения необходимо увеличить объем выборочной совокупности. Формулы расчета средних ошибок Таблица 7.2 Формулы средних ошибок
Условные обозначения в таблице:
М, m – количество равных серий соответственно в генеральной и выборочной совокупностях;
где
Следует иметь в виду, что в каждой конкретной выборке разность Предельная ошибка выборки Величина предельной ошибки определяется по формуле:
где Соответственно, формулы предельной ошибки для средней
Значения интеграла Лапласа табулированы в зависимости от значений коэффициента
Таким образом, предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью, величина которой зависит от значения коэффициента доверия t. Например, при t = 1 с вероятностью 0,683 можно утверждать, что расхождение между выборочными и генеральными характеристиками не превысит одной величины средней ошибки выборки, т.е. При t = 2 вероятность Появление ошибки в три раза большей, чем средняя ошибка выборки, маловероятно (1-0,997=0,003), и считается практически невозможным событием. Пределы, в которых с данной вероятностью В качестве доверительной вероятности обычно принимают значения вероятностей Р и соответствующие им уровни значимости Таблица 7.3 Соотношение между значениями доверительной вероятности и уровнями значимости
Например, 10 %-ный уровень значимости означает, что в 90 случаях из 100 характеристика генеральной совокупности, выявленная на основе выборки, будет лежать в пределах доверительного интервала. То есть, в 10 случаях из 100 существует риск совершить ошибку по выборочным данным при оценке генеральной совокупности. Очевидно, что чем больше значение предельной ошибки Формулы предельной ошибки позволяют определить: § доверительные интервалы, в которых будут находиться значения генеральных параметров: - генеральная средняя: - генеральная доля: § необходимую численность выборки § вероятность Наряду с абсолютной величиной предельной ошибки выборки § для средней § для доли Выборка считается репрезентативной, если Пример. В порядке случайной бесповторной выборки было обследовано n = 160 турфирм из N = 1500, и получены следующие данные об их объеме продаж за отчетный период (табл. 7.4). Таблица 7.4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 11088; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

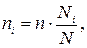
 - объем выборки из
- объем выборки из  - ой типической группы;
- ой типической группы; - объем
- объем  ,
, - число выделенных типических групп.
- число выделенных типических групп. , где
, где  - среднее квадратическое отклонение i – й группы;
- среднее квадратическое отклонение i – й группы;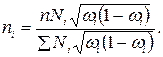
 , независимо от характера распределения генеральной совокупности. С увеличением численности выборки
, независимо от характера распределения генеральной совокупности. С увеличением численности выборки 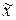 приближается к генеральной средней
приближается к генеральной средней  .
. )и генеральной средней (
)и генеральной средней ( , обладающих изучаемым признаком, и генеральной долей (р).
, обладающих изучаемым признаком, и генеральной долей (р). ;
;  .
. ;
; ;
; .
. ) и генеральных характеристик (средняя
) и генеральных характеристик (средняя 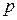 ) совокупности. Представляет собой среднее квадратическое отклонение возможных значений характеристик выборочной совокупности от характеристик генеральной совокупности.
) совокупности. Представляет собой среднее квадратическое отклонение возможных значений характеристик выборочной совокупности от характеристик генеральной совокупности. :
:
 :
:

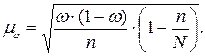
 - дисперсия признака в генеральной совокупности;
- дисперсия признака в генеральной совокупности; дисперсия доли (альтернативного признака).
дисперсия доли (альтернативного признака). , как правило, неизвестна. Поэтому в формулы ошибки выборки подставляют дисперсию выборочной совокупности
, как правило, неизвестна. Поэтому в формулы ошибки выборки подставляют дисперсию выборочной совокупности  . Это возможно, поскольку между дисперсиями генеральной и выборочной совокупностей существует следующая взаимосвязь:
. Это возможно, поскольку между дисперсиями генеральной и выборочной совокупностей существует следующая взаимосвязь: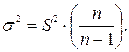
 стремится к единице, и выборочная дисперсия
стремится к единице, и выборочная дисперсия 
 сокращается, то в формулу для расчета средней ошибки включают дополнительный множитель
сокращается, то в формулу для расчета средней ошибки включают дополнительный множитель 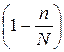 .
. для различных методов отбора приведены в табл. 7.2.
для различных методов отбора приведены в табл. 7.2.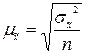




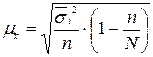
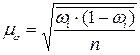
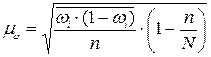








 - средняя из групповых дисперсий;
- средняя из групповых дисперсий;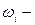 доля единиц i -й типической группы (серии) выборки, обладающих изучаемым признаком;
доля единиц i -й типической группы (серии) выборки, обладающих изучаемым признаком; - средняя из групповых дисперсий для доли.
- средняя из групповых дисперсий для доли. - межгрупповая выборочная дисперсия,
- межгрупповая выборочная дисперсия,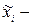 средняя в i -й серии;
средняя в i -й серии; 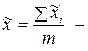 общая выборочная средняя;
общая выборочная средняя; - межгрупповая выборочная дисперсия доли, где
- межгрупповая выборочная дисперсия доли, где  - доля единиц, обладающих признаком в выборке. При равновеликих сериях
- доля единиц, обладающих признаком в выборке. При равновеликих сериях 

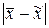 может быть меньше, больше или равна величине средней ошибки
может быть меньше, больше или равна величине средней ошибки 
 - коэффициент доверия, который определяется по таблице значений интеграла Лапласа при заданной доверительной вероятности
- коэффициент доверия, который определяется по таблице значений интеграла Лапласа при заданной доверительной вероятности  Он показывает, во сколько раз предельная ошибка выборки отличается от средней ошибки.
Он показывает, во сколько раз предельная ошибка выборки отличается от средней ошибки.

 и соответствующие им значения
и соответствующие им значения 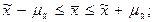
 или
или 
 (табл. 7.3)
(табл. 7.3)



 и находится вероятность).
и находится вероятность). . Она определяетсякак процентное отношение предельной ошибки выборки
. Она определяетсякак процентное отношение предельной ошибки выборки  =
= 

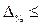 5 %.
5 %.


