
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерение сезонных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При изучении многих социально-экономических явлений часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются длительное время. Колебания особенно заметны в явлениях сезонного характера, возникают под влиянием социальных, общих экономических и других факторов. В анализе рядов динамики большое значение имеет выявление сезонных колебаний, под которыми понимаются колебания значений динамических рядов, устойчиво повторяющиеся из года в год. Причинами колеблемости уровней ряда динамики являются случайные и периодические (сезонные) колебания. Динамический ряд с сезонными колебаниями называется сезонным рядом. Изучение сезонных колебаний направлено на то, чтобы исключить их влияние на общую динамику для выявления случайной («чистой») колеблемости. Сезонные колебания (сезонная неравномерность) проявляются с различной интенсивностью в сферах производства, обращения и потребления (сельское хозяйство, транспорт, строительство, торговля, туризм и т.д.). Сезонность наносит вред экономике, что проявляется в неравномерности использования рабочей силы, производственных мощностей, транспорта и т.п. Поэтому для выявления сезонных колебаний анализируются месячные и квартальные уровни ряда динамики за год или за несколько лет. При анализе сезонности необходимо решить следующие задачи: 1) выявление наличия сезонности, численное определение ее характеристик (силы и характера в разных фазах годичного цикла); 2) характеристика факторов, вызывающих развитие сезонных колебаний; 3) оценка последствий действия сезонных колебаний; 4) математическое моделирование сезонности. Влияние сезонных колебаний полностью устранить невозможно. Но сезонные колебания, отраженные в рядах динамики, необходимо измерять. Для количественного измерения сезонных колебаний применяются методы: · метод абсолютных разностей; · метод относительных разностей; · индексы сезонности. Метод абсолютных разностей – основан на оценкеабсолютного отклонения значений средних за месяц
где:
Замечание. Если сезонность оценивается за 3 года (тридцать шесть месяцев), то О характере сезонности судят по величине и знаку значений абсолютных отклонений Метод относительных разностей является продолжением метода абсолютных разностей. В этом случае абсолютные отклонения
О величине и силе сезонности судят по величине и знаку значений относительных отклонений Вместо относительных разностей за каждый месяц может быть вычислен индекс сезонности Их расчет выполняют разными способами в зависимости от характера динамики: 1. В ряду внутригодовой динамики основная тенденция роста незначительна (не наблюдается совсем), т.е. колебания происходят вокруг некоторого постоянного уровня. В этом случае применяется способ постоянной средней. 1.1. По данным одного года:
где 1.2. По данным за несколько лет (в основном за три года) - помесячные данные одного года являются не слишком надежными для выявления закономерностей колебаний в силу элемента случайности. Поэтому на практике рекомендуется рассчитывать индексы сезонности за несколько лет (например, за три года):
2. В ряду динамики наблюдается определенная тенденция в развитии, т.е. тренд присутствует. В этом случае для выявления общей тенденции необходимо обработать фактические данные методами скользящей средней или аналитического выравнивания. Затем найти отношение фактического уровня
Измерение сезонных колебаний на базе переменных уровней тренда называется способом переменной средней. Значения индексов сезонности также позволяют судить о величине и характере сезонных колебаний. Для наглядного представления индексов сезонности в виде графика строят сезонную волну. Графическое изображение индексов сезонности наглядно показывает форму и характер «сезонной волны» относительно среднемесячного уровня за год, который принимается за 100 %. Для характеристики силы колеблемости уровней динамического ряда из-за сезонной неравномерности применяется среднее квадратическое отклонение индексов сезонности (в %) от 100 %:
Сравнение значений показателя Сезонную волну можно выделить с помощью построения модели сезонных колебаний. Аналитическая модель позволяет вывить основной закон колеблемости временного ряда и дает среднюю характеристику внутригодичных колебаний. Для анализа и прогнозирования внутригодовой динамики социально-экономических явлений может быть построена модель сезонных колебаний с помощью гармоник ряда Фурье. При аналитическом выражении изменений уровней ряда динамики используется формула:
где При При Параметры уравнения
При анализе внутригодовой динамики по месяцам значение Тогда ряд внутригодовой динамики можно записать в следующем виде (табл.8.5). Таблица 8.5
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 867; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.007 с.) |

 от общей средней
от общей средней  :
: ,
, , где
, где  - значение уровня ряда.
- значение уровня ряда.
 делят на общую среднюю
делят на общую среднюю  .
.
 .
. %,
%, - средний уровень года.
- средний уровень года.
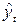 :
: .
. .
. , вычисленных за разные периоды, показывает сдвиги в сезонности.
, вычисленных за разные периоды, показывает сдвиги в сезонности. 

 - номер гармоники, определяющий степень точности (адекватности) модели (обычно
- номер гармоники, определяющий степень точности (адекватности) модели (обычно 
 и т.д.
и т.д. ;
;  ;
;  .
. . Уровни ряда представляют как части окружности с периодом
. Уровни ряда представляют как части окружности с периодом  .
.


