
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое изучение сезонностиСодержание книги
Поиск на нашем сайте
При рассмотрении квартальных или месячных данных многих cоциально-экономических явлений часто обнаруживаются определенные, постоянно повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также ряда многочисленных разнообразных факторов, которые частично являются регулируемыми. В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезонных колебаний» или «сезонных волн», а динамический ряд в этом случае называют тренд-сезонным, или просто сезонным рядом динамики. Сезонные колебания характеризуются специальным показателями, которые называются индексами сезонности (Is). Совокупность этих показателей отражает сезонную волну. Индексами сезонности являются процентные отношения фактических внутригодовых уровней к постоянной или переменной средней. Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам или кварталам. Данные за несколько лет (обычно не менее трех) берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года. Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по фактическим данным без их предварительного выравнивания. Для каждого месяца определяется средняя величина уровня, например, за три года (уi), затем из них рассчитывается среднемесячный уровень для всего ряда (у) и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, то есть: Is=
Серийная выборка Сущность серийной выборки заключается в собственно-случайном либо механическом отборе групп единиц (серий), внутри которых производится сплошное обследование. Единицей отбора при этой выборке является группа или серия, а не отдельная единица генеральной совокупности. Данный способ отбора удобен в тех случаях, когда единицы генеральной совокупности изначально объединены в небольшие более или менее равновеликие группы или серии. В качестве таких серий могут выступать упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие подобные объединения.
В связи с тем, что при серийном отборе внутри отобранных групп обследуются все без исключения единицы, внутригрупповая вариация признака не отразится на ошибках выборочного наблюдения. В то же время, обследуются не все группы, а только попавшие в выборку. Следовательно на ошибках получаемых характеристик будут отражаться различия между группами, которые определяются межгрупповой дисперсией. Поэтому средняя ошибка серийной выборки определяется по формулам:
где r - число отобранных серий; R - общее число серий. Межгрупповую дисперсию при равновеликих группах вычисляют следующим образом:
Где x i- средняя i-й серии x- общая средняя по всей выборочной совокупности. Рассмотрим следующий пример: Предположим, партия готовой продукции предприятия упакована в 100 ящиков по 30 изделий в каждом. В целях контроля соблюдения параметров технологического процесса проведена 5%-ная серийная выборка, в ходе которой отбирался каждый 20-й ящик. Все изделия, находящиеся в отобранных ящиках были подвергнуты сплошному обследованию, заключающемуся в определении их точного веса. Полученные результаты представлены в следующей таблице:
С вероятностью 0,997 требуется определить границы среднего веса изделия во всей партии.
С учетом полученной средней рассчитаем межгрупповую ди
Рассчитаем среднюю и предельную ошибки выборки(с учетом бесповторного отбора):
Так как вероятность = 0,997,следовательно коэффициент доверия t=3 Δ~=3* 9,027=27 Определим границы генеральной средней: 589-27≦Δx≦589+27 На основе результатов проведенных расчетов с вероятностью 0,997 можно утверждать, что средний вес изделия в целом по всей партии продукции находится в пределах от 562 г до 616 г.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 730; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.250 (0.009 с.) |

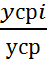 x100%, ГДЕ Усрi- средняя из фактических уровней одноименных месяцев, а Уср - общая средняя за исследуемый период
x100%, ГДЕ Усрi- средняя из фактических уровней одноименных месяцев, а Уср - общая средняя за исследуемый период


 На основе приведенных в таблице внутригрупповых средних определим средний вес изделия по выборочной совокупности:
На основе приведенных в таблице внутригрупповых средних определим средний вес изделия по выборочной совокупности:  (г)
(г) сперсию:
сперсию:
 = 9,027
= 9,027


