
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность средних величин. Виды средних величин и способы их вычисления. Расчёт среднеё арифметической, хронологической, геометрической и гармонической.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина. Средняя величина – это обобщенная типическая характеристика совокупности по изучаемому признаку в конкретных условиях места и времени. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака от- дельных единиц совокупности колеблются в ту или иную сторону под влиянием множест- ва факторов, среди которых могут быть как основные, так и случайные. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Средняя, рассчитываемая для совокупностей, состоящих из качественно однородных единиц, называется типической средней. Например, можно рассчитать среднемесячную заработную плату работника той или иной профессиональной группы (шахтера, врача библиотекаря). Разумеется, уровни месячной заработной платы шахтеров в силу различия их квалификации, стажа работы, отработанного за месяц времени и многих других факторов отличаются друг от друга, так и от уровня средней заработной платы. Однако в среднем уровне отражены основные факторы, которые влияют на уровень заработной платы, и взаимно погашаются различия, которые возникают вследствие индивидуальных особенностей работника. Средняя заработная плата отражает типичный уровень оплаты труда для данного вида работников. Получению типической средней должен предшествовать анализ того, насколько данная совокупность качественно однородна. Если совокупность состоит их отдельных частей, следует разбить ее на типические группы (средняя температура по больнице).
Средние величины, используемые в качестве характеристик для неоднородных совокупностей, называются системными средними. Например, средняя величина валового внутреннего продукта (ВВП) на душу населения, средняя величина потребления различных групп товаров на человека и другие подобные величины, представляющие обобщающие характеристики государства как единой экономической системы.
Средняя должна вычисляться для совокупностей, состоящих из достаточно большого числа единиц. Соблюдение этого условия необходимо для того, чтобы вошел в силу закон больших чисел, в результате действия которого случайные отклонения индивидуальных величин от общей тенденции взаимно погашаются.
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. Наиболее часто применяются средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и средняя кубическая. Перечисленные средние относятся к классу степенных средних и объединяются общей формулой:
Где x̅ – среднее значение исследуемого признака; m – показатель степени средней; xᵢ– текущее значение (варианта) осредняемого признака; n – число признаков.
Различают следующие виды степенных средних: · средняя гармоническая; · средняя геометрическая; · средняя арифметическая; · средняя квадратическая; · средняя кубическая и тд. 1. Средняя арифметическая А) Средняя арифметическая простая рассчитывается по формуле:
Б) Средняя арифметическая взвешенная рассчитывается по формуле: х 2. Средняя хронологическая (если моментов больше двух и интервалы между ними равны): x̅= Например: на 1.01 на 1.02 на 1.03 на 1.04 Остатки материалов 90 95 81 70 Среднемесячные остатки материалов на складе составят: х̅= 3. Средняя геометрическая (используется для анализа динамики явлений и позволяет определить средний коэффициент роста) х̅= Например: Количество зарегистрированных преступлений за 4 года возросло в 1,57 раза, в т. ч. за 1-й – в 1,08 раза, за 2-й – в 1,1 раза, за 3-й – в 1,18 и за 4-й – в 1,12 раза. Тогда среднегодовой темп роста количества преступлений составляет: х̅= т.е. число зарегистрированных преступлений ежегодно росло в среднем на 12%. 4. Средняя гармоническая (применяется если статистическая информация не содержит частот f по отдельным вариантам x совокупности, а представлена как их произведение) А) Средняя гармоническая простая: x̅= Б) Средняя гармоническая взвешенная: х̅= Пример: Даны данные по двум предприятиям:
Cреднее значение реализованной продукции на одного работника определяется по формуле средней гармонической взвешенной: х̅=
Виды статистического наблюдения. План и программа. Различают следующие виды наблюдения: В зависимости от охвата единиц совокупности: 1. Сплошное наблюдение – регистрации подлежат все единицы изучаемой совокупности (перепись населения). 2. Несплошное наблюдение охватывает определённую часть изучаемой совокупности и в свою очередь подразделяется на:
По времени регистрации наблюдения: 1. Непрерывное (текущее) наблюдение ведется систематически, постоянно, непрерывно, осуществляется путём непрерывной регистрации фактов по мере их возникновения. 2. Прерывное наблюдение производится либо регулярно через равные промежутки времени, либо по мере надобности и подразделяется на:
По источнику сведений различают непосредственное наблюдение, документальное наблюдение и опрос.
В статистике применяются следующие способы сбора сведений:
План статистического наблюдения состоит из двух частей, первая включает программно-методологические вопросы, а вторая организационные вопросы.
Программа наблюдения - это перечень признаков, подлежащих регистрации при проведении статистического наблюдения. К программе наблюдения предъявляется ряд требований, которым она должна удовлетворять, а именно:
а) программа должна включать только существенные признаки, характеризующие изучаемый объект;
Вопросы программы могут дополняться статистическим подсказом, т.е. вариантами ответов. Подсказ может быть закрытым или открытым. Закрытый подсказ подразумевает ряд ответов, из которых респондент должен выбрать один или несколько" При открытом подсказе респондент может выбрать один или несколько ответов из предлагаемого перечня или сформулировать на специально выделенном поле формуляра свой собственный ответ. Для записи ответов на вопросы программы наблюдения разрабатывается формуляр наблюдения. В процессе статистического наблюдения собирается первичная информация, которая затем подвергается систематизации обобщению и анализу. От качества первичной информации зависит успех всего исследования, поэтому к информации предъявляется ряд требований:
Сопоставимость - сравнимость данных с прошлыми исследованиями. Сопоставимость обеспечивается использованием одних и тех же единиц измерения, наблюдением в одно и тоже время и по единой методологии.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 871; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |


 ; или х̅=
; или х̅= 
 =
= 

 =85,3 тыс
=85,3 тыс
 = 1,12
= 1,12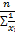

 = 825
= 825


