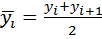Виды рядов динамики. Правила построения рядов динамики.

Ряды динамики подразделяются на моментные, интервальные и ряды средних величин.

Моментные ряды динамики отображают состояние исследуемых процессов на определенные даты времени.

Интервальные ряды динамики отображают итоги развития или функционирования исследуемых процессов за отдельные периоды времени.

Для характеристики процесса за определенный период рассчитывают средний уровень из всех членов динамического ряда.

К составлению рядов динамики предъявляются следующие требования.

 

1. Периодизация развития, т. е. расчленение его во временна однородные этапы, в пределах которых показатель подчиняете одному закону развития. Это, по существу, типологическая группировка во времени.

Методами периодизации являются:

• исторический метод, когда периодизация осуществляется на основе «узаконенной» структуры динамики

• метод параллельной периодизации: предполагается, что существует показатель X, которому соответствует динамический ряд Xt определяющий поведение исследуемого показателя У, тогда в рол однокачественных периодов развития У можно взять периоды X.

• методы многомерного статистического анализа. Част требуется выделить однокачественные периоды в развитии явлений или процессов, таких, например, как здоровье населения, развитие сельскохозяйственного производства и др., получить адекватное отображение которых с помощью одного лишь показателя трудно. Очевидно, что для эквивалентного описания столь сложного, интегрированного явления, как здоровье, нельзя ограничиться комплексными показателями смертности, продолжительности жизни, заболеваемости.

Однокачественность уровней временного ряда означает, что в пределах всего изучаемого периода, к которому относятся уровни, должна быть проведена типологическая группировка. После выделения однородных групп можно использовать и анализировать уровни ряда. Это требование формулируется как обеспечение сравнимости по структуре совокупности, для чего обычно применяется стандартная, нормативная структура.

 

2. Сопоставимость статистических данных — по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета.

Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах, а сопоставимость по кругу охватываемых объектов предполагает сравнение совокупностей с равным числом элементов. Территориальная и объемная сопоставимость обеспечивается смыканием рядов динамики, при лом либо абсолютные уровни заменяются относительными, либо делается пересчет в условные абсолютные уровни. Не возникает особых сложностей при обеспечении сопоставимости данных по единицам измерения; стоимостная сравнимость достигается системой сопоставимых цен. Трудности могут появиться при сравнении данных по моменту регистрации. В большей степени это относится к сезонным явлениям. В таких случаях даже регистрации на одну и ту же дату часто бывает недостаточно для обеспечения сопоставимости

3. Соответствие величины временных интервалов интенсивности изучаемых процессов. Чем больше вариация уровней времени, тем чаще следует делать замеры. Соответственно дл стабильных процессов интервалы можно увеличить. Так, перепись населения достаточно проводить один раз в десять лет; уч национального дохода, урожая — раз в год, ежедневно регистрируются курсы покупки и продажи валют, ежечасно — температур воздуха и т. п.

4. Упорядоченность числовых уровней рядов динамики времени. Не допускается анализ рядов с пропусками отдельных уровней; если же такие пропуски неизбежны, то их восполняют" условными расчетными значениями.

 

Вычисление среднего уровня в рядах динамики

Интервальные ряды динамики

Уровни интервального ряда характеризуют результат изучаемого процесса за период времени: производство или реализация продукции (за год, квартал, месяц и др. периоды), число принятых на работу, число родившихся и.т.п. Уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени.

Средний уровень в интервальных рядах динамики () исчисляется по формуле средней арифметической простой:

, где y — уровни ряда (y₁, y₂ ,...,y_n),

n — число периодов (число уровней ряда).

Пример: Рассмотрим методику расчета среднего уровня интервального ряда динамики на примере данных о продаже сахара в России.

Годы	Продано сахара, тыс. тонн

тыс. тонн - это среднегодовой объем реализации сахара населению России за 1994-1996 гг.

 

Моментные ряды динамики

Уровни моментных рядов динамики характеризуют состояние изучаемого явления на определенные моменты времени. Каждый последующий уровень включает в себя полностью или частично предыдущий показатель. Так, например, число работников на 1 апреля 1999 г. полностью или частично включает число работников на 1 марта.

Если сложить эти показатели, то получим повторный счет тех работников, которые работали в течение всего месяца. Полученная сумма экономического содержания не имеет, это расчетный показатель.

В моментных рядах динамики с равными интервалами времени средний уровень ряда исчисляется по формуле средней хронологической:

Пример: Рассмотрим методику такого расчета по следующим данным о списочной численности работников предприятия за 1 квартал.

Дата	Число работников
01.янв
01.фев
01.мар
01.апр

человек

В моментных рядах динамики с неравными интервалами времени средний уровень ряда исчисляется по формуле средней арифметической взвешенной. В качестве весов средней принимается продолжительность времени (t- дни, месяцы). Выполним расчет по этой формуле.

 

 

Списочная численность работников предприятия за октябрь такова:

 

Дата	Число работников
01.окт
07.окт
12.окт
21.окт

человек.

В тех случаях, когда имеем моментный ряд динамики с неравными интервалами времени, а конкретные даты изменения показателя неизвестны исследователю, то сначала надо вычислить среднюю величину () для каждого интервала времени по формуле средней арифметической простой, а затем вычислить средний уровень для всего ряда динамики, взвесив исчисленные средние величины продолжительностью соответствующего интервала времени . Формулы имеют следующий вид:

, где