
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значения коэффициента доверияСодержание книги
Поиск на нашем сайте
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Так, при случайном повторном отборе средняя ошибка определяется по формуле а при бесповторном: где s2 - выборочная (или генеральная) дисперсии; s - выборочное (или генеральное) среднее квадратическое отклонение; n - объем выборочной совокупности; N - объем генеральной совокупности.
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для генеральной средней такие пределы устанавливаются на основе следующих соотношений:
где
Пример. В городе проживает 250 тыс. семей. Для определения среднего числа посещений торгового центра «Всё для вас» за месяц была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу посещений центра:
С вероятностью 0,954 необходимо определить пределы, в которых будет находиться среднее число посещений в генеральной совокупности. Решение. Вначале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).
Следовательно, пределы генеральной средней:
Таким образом, с вероятностью 0,954 можно утверждать, что среднее число посещений торгового центра «Все для вас» семьями города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три посещения центра в месяц.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака. В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:
где
Тогда, например, при собственно-случайном повторном отборе для определения средней (стандартной) ошибки выборки используется следующая формула:
Соответственно, при бесповторном отборе:
Предельная ошибка доли признака: Пределы доли признака в генеральной совокупности р выглядят следующим образом:
2) Анализ показателей ряда динамики (вычисление абсолютных приростов, темпов роста и прироста, абсолютное содержание 1 % темпа прироста). При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут: Расчет показателей динамики представлен в следующей таблице.
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях. Система средних показателей динамики включает:
где n или (n +1) – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Yi (1 = 1, 2,..., n или 1 = 0, 1, 2,..., n). Средний абсолютный прирост рассчитывается по формулам в зависимости от способа нумерации интервалов (моментов).
Средний темп роста:
где Средний темп прироста (%) определяется по единственной методологии:
P.S.Пример задачи сами придумайте;) Например как мы делали задание с переписью населения;)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

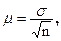
 ,
, ,
, и
и  - генеральная и выборочная средняя соответственно;
- генеральная и выборочная средняя соответственно; - предельная ошибка выборочной средней.
- предельная ошибка выборочной средней.


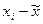


 (посещения);.
(посещения);.  .
.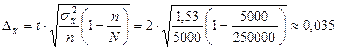 .
. .
. ,
, - доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
- доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки. .
. .
.
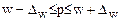
 *
*






 .
.
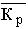 – средний коэффициент роста, рассчитанный как
– средний коэффициент роста, рассчитанный как  . Здесь Кцеп – цепные коэффициенты роста;
. Здесь Кцеп – цепные коэффициенты роста;



