
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели изменения уровней рядов динамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При анализе изменений явления во времени на практике часто определяют средние показатели, в том числе средний уровень ряда. Средний уровень - это важнейшая обобщающая характеристика для рядов динамики, изменение которых стабилизировалось в исследуемом периоде и при этом подвержено ощутимым случайным колебаниям. Средний уровень ряда определяется по-разному для моментных и интервальных рядов. При этом следует обратить внимание на то, какие -равностоящие или не равностоящие во времени - уровни наблюдаются в ряду динамики. Для интервальных рядов динамики с равностоящими во времени уровнями расчет среднего уровня проводится по формуле простой средней арифметической:
где n - число уровней или длина ряда; В случае интервальных рядов динамики с не равностоящими во времени уровнями для расчета среднего уровня используется формула взвешенной средней арифметической, где в качестве весовых коэффициентов используется продолжительность интервалов времени (число периодов времени, при которых значение уровня не изменяется) находится по формуле:
Для моментных рядов динамики с равностоящими во времени уровнями средний уровень (так называемая средняя хронологическая) находится по формуле:
В случае моментных рядов динамики с не равностоящими во времени уровнями средний уровень определяется по формуле средней скользящей взвешенной:
где у1,у2....уn— уровни рядов динамики; t — продолжительность интервала времени между смежными уровнями. Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста. Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста. Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, — базисным. Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными. Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными. Важнейшим статистическим показателем анализа динамики является абсолютное изменение — абсолютный прирост (сокращение). Абсолютное изменение характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста. Абсолютный прирост Абсолютный прирост (цепной): (базисный):
где yi — уровень сравниваемого периода; yi-1 - уровень предшествующего периода; у - уровень базисного периода (в данном случае начальный уровень ряда). Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени
Для характеристики интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы называется коэффициентом роста, а в процентах — темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения. Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число. Коэффициент роста (цепной); Коэффициент роста (базисный):
Темп роста (цепной): Темп роста (базисный):
Итак Tp=Kp Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период базисного темпа роста на предыдущий равно соответствующему цепному темпу роста. Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Теми прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста). Темп прироста (цепной): Темп прироста (базисный):
Темп прироста (сокращения) можно получить также и из темпа роста, выраженного в процентах, если из него вычесть 100%, а коэффициент получается вычитанием единицы из коэффициента роста: Tпр=Tp-100 (1.8.9) Kпр=Kp-1 (1.8.10) абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы, правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:
Абсолютное значение одного процента, прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста. В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем темп прироста соответствующего периода по сравнению с базисным. Для более глубокого понимания характера явления необходимо показатели динамики анализировать комплексно, совместно. Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний годовой абсолютный прирост как среднюю арифметическую простую:
где m — число цепных абсолютных приростов ( Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост ( применим следующую формулу:
где n — число уровней ряда динамики в изучаемом периоде, включая базисный. Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. Средний темп роста (снижения) — обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (снижения) применяется определяющий показатель — произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему правилу нужно применять среднюю геометрическую. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах, (
где m - число цепных коэффициентов роста; Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода у„ на уровень базисного периода у. Тогда формула для расчета среднего коэффициента роста для равностоящих радов динамики (по «базисному способу»):
где п — число уровней ряда динамики в изучаемом периоде, включая базисный. Для расчета средних коэффициентов роста по формуле (6.15) нет необходимости знать годовые темпы. Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:
где
Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100 %, "а средний темп прироста — отрицательной величиной. Отрицательный темп прироста При анализе развития явлений, отражаемых двумя динамическими рядами, представляет интерес сравнение интенсивностей изменения во времени обоих явлений. Такое сопоставление интенсивностей изменения производится при сравнении динамических рядов одинакового содержания, но относящихся к разным территориям (странам, республикам, районам и т.п.), или к различным организациям (министерствам, предприятиям, учреждениям), или при сравнении радов разного содержания, но характеризующих один и тот же объект. Например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в Российской Федерации и других странах. Сравнительные характеристики направления и интенсивности роста одновременно развивающихся во времени явлений определяются приведением рядов динамики к общему (единому) основанию и расчетом коэффициентов опережения (отставания). Ряды динамики (в которых возникают, например, проблемы сопоставимости цен сравниваемых стран, методики расчета сравниваемых показателей и т.п.) обычно приводят к одному основанию, если они не могут быть решены другими методами. По исходным уровням нескольких рядов динамики определяют относительные величины — базисные темпы роста или прироста. Принятый при этом за базу сравнения период времени (дата) выступает в качестве постоянной базы расчетов темпов роста для каждого из изучаемых радов динамики. В зависимости от целей исследования базой может быть начальный, средний или другой уровень ряда. Сравнение интенсивности изменений уровней рядов во времени возможно с помощью коэффициентов опережения (отставания), представляющих собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени:
Где Коэффициенты опережения (отставания) могут быть исчислены на основе сравнения средних темпов роста (или прироста) двух динамических радов за одинаковый период времени:
Где динамики соответственно. Коэффициент опережения (отставания) показывает, во сколько раз быстрее растет (отстает) уровень одного рада динамики по сравнению с другим. При этом сравнении темпы должны характеризовать тенденцию одного направления. Таблица 1.8.1. Основные показатели динамики
Компоненты временных рядов В практике исследования динамики явления и прогнозирования принято считать, что значения уровней временных рядов могут содержать следующие компоненты: - тренд; - сезонную компоненту; - циклическую компоненту; - случайную компоненту. Под трендом понимают изменение, определяющее общее направление развития, основную тенденцию временного ряда. Это систематическая составляющая долговременного действия. Наряду с долговременными тенденциями во временных рядах часто возникают более или менее регулярные колебания - периодические составляющие рядов динамики. Если период колебания не превышает одного года, то их называют природно-климатические условия. В сезонных колебаниях прослеживается устойчивая годовая периодичность. При большом периоде колебания считают, что во временных радах имеет место циклическая составляющая. Примерами могут служить циклы деловой активности, демографические, инвестиционные и другие циклы. Если из временного ряда удалить тренд и периодические составляющие, то останется нерегулярная компонента. Экономисты разделяют факторы, под воздействием которых формируется нерегулярная компонента, на два вида: - факторы резкого, внезапного действия; - текущие факторы. Факторы первого вида (например, стихийные бедствия, войны, кризис и т.п.), как правило, вызывают более значительные отклонения, Факторы второго вида вызывают случайные колебания, являющиеся результатом действия большого числа побочных причин. Влияние каждого из текущих факторов незначительно, но ощущается их суммарное действие. Если временной ряд представляется в виде суммы соответствующих компонент, то полученная модель носит название аддитивной (6.19), если в виде произведения - мультипликативной (6.20); также можно выделить еще один вид модели - смешанного типа (6.21): yt=ut+st+vt+ yt=ut x st x vt x yt=ut x st x vt+ где yt - уровни временного ряда; ut - трендовая компонента; st- сезонная компонента; vt - циклическая компонента;
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 702; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.012 с.) |

 (1.8.1.)
(1.8.1.) - уровень ряда динамики (t=1,2,...,n)
- уровень ряда динамики (t=1,2,...,n) (1.8.2)
(1.8.2) (1.8.3)
(1.8.3) (1.8.4)
(1.8.4) (1.8.5a)
(1.8.5a)  (1.8.5б)
(1.8.5б)
 (1.8.6a)
(1.8.6a)  (1.8.6б)
(1.8.6б) (1.8.7a)
(1.8.7a) 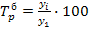 (1.8.7б)
(1.8.7б) .
. , а частное от деления последующего
, а частное от деления последующего (1.8.8a)
(1.8.8a)  (1.8.8б)
(1.8.8б) (1.8.11)
(1.8.11) (.1.8.12)
(.1.8.12) ) в изучаемом периоде.
) в изучаемом периоде. ). Для случая равных интервалов
). Для случая равных интервалов (1.8.13)
(1.8.13)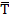 =
=  • 100), то для равноотстоящих радо» динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):
• 100), то для равноотстоящих радо» динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»): (1.8.14)
(1.8.14) ,...,
,..., 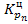 — цепные коэффициенты роста.
— цепные коэффициенты роста. (1.8.15)
(1.8.15)
 (1.8.16)
(1.8.16) - средний темп прироста
- средний темп прироста - средний коэффициент прироста.
- средний коэффициент прироста. , представляет собой средний темп сокращения и характеризует среднюю относительную скорость снижения уровня.
, представляет собой средний темп сокращения и характеризует среднюю относительную скорость снижения уровня. (1.8.17a)
(1.8.17a)  (1.8.17б)
(1.8.17б)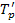 ,
,  — базисные темпы роста и прироста первого и второго рядов динамики (соответственно).
— базисные темпы роста и прироста первого и второго рядов динамики (соответственно). (1.8.18)
(1.8.18)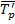 ,
,  — средние темпы роста первого и второго радов
— средние темпы роста первого и второго радов
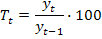





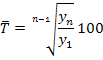

 t (1.8.19)
t (1.8.19) t (1.8.20)
t (1.8.20)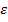 t - случайная компонента.
t - случайная компонента.


