
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение типовых задач к теме 1.5.: Обобщающие показатели.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Задача № 1. Имеются данные о производстве мыла за отчетный и базисный
Определите динамику производства мыла в натуральном измерении и в условно-натуральном измерении (40%-го мыла). Решение: 1) Динамика производства мыла в натуральном выражении = (63 + 65 + 95) / (60 + 63 +82) = 223 / 207 = 1, 077 или 107, 7% 2) Для определения объема продукции в условно-натуральном измерении мыло 40% - коэффициент = 1,0 мыло 60% - коэффициент = 60/40 = 1,5 мыло 80% - коэффициент = 80/40 = 2,0 Тогда динамика производства мыла в условно-натуральном измерении равна = (63×1, 0 + 65×1, 5 + 95×2, 0) / (60×1, 0 + 63×1, 5 +82×2, 0) = (63 + 97, 5 + 190) / (60 + 97, 5 + 64) = 1, 090 или 109, 0. Задача № 2. По плану на 2002 год рост производства продукции по предприятию должен был составить 104,3%. Фактический рост выпуска продукции в 2002году составил 104,8%. Как был выполнен план производства продукции на предприятии? Решение: Исходя из взаимосвязи относительных величин планового задания, выполнения плана и динамики, искомая относительная величина выполнения плана будет равна частному от деления относительной величины динамики на относительную величину планового задания 1,048:1,043=1,004 или 100,4%. Задача № 3. Определите относительные величины структуры по данным о количестве проданных квартир в стране.
Задача № 4. На начало учебного года численность студентов высших учебных заведений Республики составляла 67,6 тыс. чел., а численность всего населения 3,7 млн. чел. Определите относительную величину интенсивности (количество студентов на 1000 человек населения (о/оо)). Решение: 67,6 тыс. чел. студентов; 3700 тыс. чел. населения х 1000=18о/оо (18 человек на 1000 человек населения). Задача № 5. Пассажирооборот отдельных видов транспорта общего пользования в Республике составил, тысяч пассажиро-километров.
Определите, сколько пассажиро-километров каждого вида транспорта приходится на 1000 пассажиро-километров железнодорожного транспорта. К какому виду относительных величин относится исчисленные показатели? Решение:
Рассчитанные показатели в промилле (о/оо) являются относительными величинами координации, т.к., характеризуют соотношение частей целого между собой. Задача № 6. Средняя урожайность картофеля в Российской Федерации составила 106 ц/га, а в Республике Татарстан - 122 ц/га. Сравните урожайность картофеля в Российской Федерации с урожайностью в Республике Татарстан. Решение: Относительная величина сравнения 106/122×100% = 86, 9% Задача № 7. В двух бригадах выработка одноименной продукции за смену характеризуется следующими данными:
Определите в какой бригаде и на сколько выше средняя выработка продукции на одного рабочего. Какой вид средней выработки использован для расчета в каждом случае? Решение: Для определения средней выработки по первой бригаде используется формула средней арифметической простой x = ∑xn/n, где х – выработка в п каждой группе рабочих, а n – число групп. X = (20 + 25 + 30 +40)/4 = 29 (шт.), т.к. каждый вариант выборки встречается равное (по 25) число раз. Для определения средней выработки по второй бригаде используется формула средней арифметической взвешеннойx = ∑xf/f, где х – выработка в каждой группе рабочих, а f – число рабочих в каждой группе. Х = Следовательно, средняя выработка в бригадах одинаковая. Задача № 8. Требуется вычислить среднюю цену продукта «А» в отчетном и базисном периодах на основании данных по двум рынкам города:
Решение: Средняя цена Х = Выручка, руб./Продано, кг В базисном периоде среднюю цену продукта определяем по средней арифметической взвешенной, т.к. знаменатель дроби известен (количество проданного продукта), а числитель (выручку) определяем путем умножения цены 1 кг продукта на количество в кг.
Среднюю цену в отчетном периоде следует вычислять по средней гармонической взвешенной, т.к. числитель дроби известен (выручка), а знаменатель дроби (продано, кг) можно определить путем деления суммы выручки по каждому рынку на цену 1 кг.
Задача № 9. Имеются данные о выполнении плана на двух предприятиях за два периода:
Необходимо определить средний процент выполнения плана на двух предприятиях в базисном и отчетном периодах. Решение: Т.к. процент выполнения это отношение: фактический выпуск / плановый объем, то в базисном периоде средний процент выполнения плана определяем по средней гармонической взвешенной, т.к. числитель дроби известен (фактический выпуск), а знаменатель дроби (плановый объем) находим как частное от деления фактического выпуска на коэффициент выполнения плана.
В отчетном периоде средний процент выполнения плана определяем по средней арифметической взвешенной, т.к. знаменатель дроби известен (плановый объем), а числитель дроби можно определить как произведение коэффициента выполнения плана по каждому заводу на плановый объем продукции.
Задача № 10. Рабочие завода распределены по возрасту следующим образом:
Определите моду и медиану: Решение:
Задача № 11. На основании нижеследующих данных определите: а) средний размер основных промышленно-производственных фондов на один завод (упрощенным способом);
Т.к. интервал группировки равный, для расчета используем упрощенный метод моментов Х = тi - i + A Средний размер основных фондов
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 =
=  =
=  = 29 (шт.), т.к. каждый вариант выработками встречается разное число раз.
= 29 (шт.), т.к. каждый вариант выработками встречается разное число раз. =
=  =
=  = 62, 06 руб.
= 62, 06 руб. =
=  =
=  =
=  = 61, 51 руб.
= 61, 51 руб.
 100 = 100, 6%
100 = 100, 6% =
=  =
=  × 100 =
× 100 =  × 100 = 10, 0%
× 100 = 10, 0% =
=  +
+ 
 (
( ) = 20+10×
) = 20+10×  = 20 + 10×
= 20 + 10× 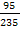 = 24 (года), т.к. модальный интервал 20-30.
= 24 (года), т.к. модальный интервал 20-30. =
=  ×
×  = 20+10×
= 20+10×  = 20+10×
= 20+10×  = 24, 5 (лет), т.к. медианный интервал 20-30
= 24, 5 (лет), т.к. медианный интервал 20-30 )
i=2
)
i=2
 )
)
 =
=  =
=  = 0, 35, где
= 0, 35, где  момент первой степени, тогда
момент первой степени, тогда 
 0, 35×2+9=9,7 (млн. руб.).
0, 35×2+9=9,7 (млн. руб.).


