
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение типовых задач к теме 1.8.: Статистическое изучение динамики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача №1. По данным о вводе в действие жилых домов (таблица 1) необходимо рассчитать 1, Цепные, базисные и средние: а) абсолютные приросты; б) темпы роста; в) темпы прироста; 2. Абсолютное значение 1 % прироста. Таблица 1. Ввод в действие жилых домов, млн. кв.м.
Решение: Представим расчет цепных и базисных абсолютных приростов, темпов роста, темпов прироста в таблице 2
Для получения обобщающих показателей динамики развития определим средние характеристики % средний абсолютный прирост, средний темп роста и средний темп прироста. Средний абсолютный прирост равен:
то есть, в среднем ежегодно общая площадь вводимого жилья уменьшалась на 0,525 млн. кв. м. Определим средний темп роста:
то есть, в среднем ежегодно строительство жилья составляло 91,47 % уровня базисного года. Средний темп пророста Задача №2. Имеются следующие данные о поголовье крупного рогатого скота на 1 января: Годы 1-ый 2-ой 3-ий 4-ый Млн. голов 60,4 61,0 60,3 69,2 Решение: так как это моментный ряд с равным интервалом (1 год), то средний уровень ряда определяется по средней хронологической:
Задача №3. Имеются данные об уровне запасов картофеля на начало года: Млн. т. 2103 2170 1584 Решение: так как это моментный ряд с неравным интервалом, то среднегодовой уровень определяется по формуле средней скользящей взвешенной:
Задача №4. Численность работников организации с 1 января до 9 января была 180 человек, 9 января были приняты 7 человек, 15 января уволены 2 человека, 25 января были приняты 5 и уволены 10. До конца месяца изменений не было. Определите среднюю списочную численность работников организаций в январе. Решение: так как это интегральный рад с неравным интервалом, то средний уровень ряда определяем по средней арифметической взвешенной:
Решение типовых задач к вопросу: Статистические методы прогнозирования рядов динамики. Задача №1 Проверка гипотезы на существование тренда. В таблице 1. представлены годовые данные об урожайности зерновых культур. Таблица 1 Урожайность зерновых культур п/га
Определить: существует ли тенденция в исследуемом процессе. Решение: Процесс формирования серий показан в таблице 2. Во второй строке этой таблицы в соответствии указан «+», если последующее значение уровня ряда больше предыдущего, «-», если - меньше. Таблица 2 Формирование серий
Анализ полученной последовательности знаков позволил число серий v(21)=8 протяженность самой длинной серии Табличное значение (см.табл.1.8.2.) Делаем проверку. Для этого сначала определим значение для правой части первого неравенства:
Тогда проверка выполнения условий показывает, что оба неравенства не выполняются. Следовательно, нулевая гипотеза отвергается, динамика временного ряда характеризуется наличием систематической составляющей - в изменении урожайности присутствует динамика. Задача № 2. Методы сглаживания временных рядов. По данным об урожайности (табл. 1) за 16 лет рассчитайте: трех-, семилетние скользящие средние и графически сравните результаты; пятилетнюю взвешенную скользящую среднюю.
Таблица1. Урожайность пшеницы, ц/га
Решение: 1. Результаты расчетов представлены в табл.2. Таблица 2. Расчет скользящих средних
При трехлетней скользящей средней (i=3)
При семилетней скользящей средней (i=7)
2. Для вычисления значений пятилетней взвешенной скользящей средней воспользуемся таблицей 1. Тогда
И т.д. Задача № 3, Пусть сглаживание осуществляется по пятичленной скользящей средней (I=5), причем аппроксимация осуществляется квадратичным полиномом (m=2). Требуется определить весовые коэффициенты для восстановления двух последних уровней рада. Решение: Осуществим перенос начала координат в середину активного участка: t=-2;-1;0;+1;+2; После этого система нормальных уравнений примет вид:
Из первого и третьего уравнений определим выражение для коэффициента a0:
или в символической записи Выразим теперь остальные неизвестные параметры из системы уравнений (1.8.54):
Полученные выражения для коэффициентов a0,a1,a2, подставим в уравнение сглаживающего квадратического полинома:
Последовательно подставляя в это выражение t=1;2, получим весовые коэффициенты для восстановления последних уровней ряда: - при t=l (восстановление предпоследнего уровня ряда)
-при t=2(восстановление последнего уровня ряда)
Если последними пятью уровнями ряда были 0; 1; 4; 9; 16, то восстановление двух последних значений осуществлялось бы следующим образом: - при t=1
-при t=2
Задача №4 Методы аналитического выравнивания и прогнозирования временных радов. Необходимо выравнить рад динамики с помощью уравнения линейного тренда y=a0+a1
Решение: Параметры a0 и a1 находим по формулам:
n=9 Подставляя в уравнение yt=410,12-6,63t вместо t числовые значения текущих лет (дней, месяцев) - 1,2,3,...n получим выравненные значения yt то есть
Задача №5. Методы аналитического выравнивания и прогнозирования временного ряда. В таблице 1. представлен ряд динамики условного экономического показателя (у) за девять лет (t).
Рассчитать доверительный интервал прогноза по уровню тренда. Решение: По данным таблицы 1. построим уравнение линейного тренда. y=a0+a1 Расчет параметров a0,a1 производится по методу наименьших квадратов, для чего строится система нормальных уравнений:
В результате получим линейное уравнение у = 410,12 — 6,63 t ,R2 =0,716 Последовательно подставляя в полученное уравнение вместо t его численные значения 1-год, 2-год,3-год и т.д. получим расчетные значения
Колеблемость уровней динамического ряда относительно тренда определяется по формуле
Тогда доверительный интервал для тренда составит:
где ta- табличное значение критерия Стьюдента. При a=0,05 и числе степеней свободы равном 7,для нашего примера, ta = 2,365 и доверительный интервал для тренда равен
Если распространить этот интервал прогноза на следующий 10-й год (t=10), то он составит
343,4-25,5≤yt=10≤343,8+25,5 318,3≤yt=10≤369,3
Задаче № 6. Методы изучения сезонных колебаний. В таблице 1 представлены условные данные о ежемесячном выпуске продукция за три года. Необходимо рассчитать индекс сезонности. Таблица 1. Производство условного продукта по месяцам в расчет индексов.
Решение: Для каждого месяца рассчитывается средняя величина уровня. В нашем примере за три года (
где Средний индекс сезонности для 12 месяцев должен быть равен 100%, тогда сумма индексов должна составлять 1200. В нашем примере это отношение равно 1200,4 (небольшая погрешность — следствие округления). Задача № 7. Упрощенные приемы прогнозирования. Прибыть за год характеризуется данными, приведенными в таблице 1.
Оценим существенность различий в дисперсиях: F=0,92/0,86=1,07 при табличном значении 5,05 (для а =0,05 и при числе степеней свободы 5 и 5). Дисперсии можно признать равными. Тогда оценим существенность расхождения в среднемесячных уровнях прибыли за каждое полугодие по t-критерию Стьюдента:
Произведя дальнейшие вычисления, находим, что t= 1,84. Это меньше i т= 2,23. Следовательно, с вероятностью 0,95 можно признать, что тенденции в ряду динамики нет. Прогноз по стационарному ряду основан на предположении о неизменности в будущем среднего уровня динамического ряда, т.е. yp=
где yp - прогнозное значение. Так как средний уровень динамического ряда имеет погрешность как выборочная средняя и, кроме того, отдельные уровни ряда колеблются вокруг среднего значения, принято прогноз давать в интервале:
где
n- длина динамического ряда.
где дисперсия.
ta=0,05,n-1=11=2,201 Тогда ошибка прогноза составит: 2,201 Соответственно прогноз прибыли на январь следующего года окажется таким: 61
Задача № 8. Метод экспоненциального сглаживания. Рассчитайте экспоненциальную среднюю для временного ряда курса акций фирмы IBM (таблица 1). В качестве начального значения экспоненциальной средней возьмите среднее значение из пяти первых уровней ряда. Расчеты проведите для двух различных значений параметров адаптации а: а) а=0,1; б) а=0,5. Курс акций фирмы IBM долл. США Таблица 1.
Решение: 1. Определим
Найдем значения экспоненциальной средней при а=0,1
И т.д. Результаты расчетов представлены в табл.2. Проведем аналогичные расчеты для а=0,5.
Результаты расчетов также представлены в таблице 2. Экспоненциальные средние Таблица2.
При а=0,1 экспоненциальная средам носит более гладкий характер,так как в этом случае в случае в наибольшей степени поглощаются случайные колебания временного ряда. Задача №9. Метод гармонических весов. В таблице 1 дан ряд динамики производства продукции за 9 лет. Таблица 1
Решение: Предварительно ряд динамики был проверен на выполняемость предпосылок, на которых базируется метод. Далее находим параметры уравнений отдельных фаз движения скользящего тренда. В нашем примере к=3, тогда находим: (9-3+1)=7 уравнений:
С помощью полученных уравнений определяем значение скользящего тренда. При t=1 имеем одно значение уравнения
При t=2 имеем два значения
Отсюда Аналогично находим все значения:
Затем были рассчитаны приросты по формуле (7. 27)
и гармонические веса по формуле (7.31)
Гармонические коэффициенты получим по формуле (7.32): С2 = 0,0156 С3 = 0,0335 С4 = 0,0543 С5 = 0,0793 С6 =0,1106 С7= 0,1522 С8= 0,2147 С9 = 0,3397 Все эти коэффициенты удовлетворяют условиям 7.29, Используя формулу 7.28. находим средний абсолютный прирост ( y10=20,51 y11=22,02 y12= 23,53
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 3233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.10.9 (0.011 с.) |

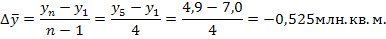
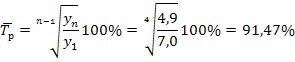
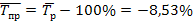 то есть в среднем ежегодно строительство жилья снижалось на 8,53 %.
то есть в среднем ежегодно строительство жилья снижалось на 8,53 %.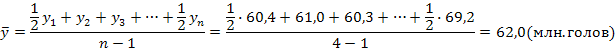

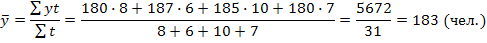
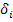
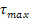 (21) = 6
(21) = 6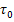 (21) = 6
(21) = 6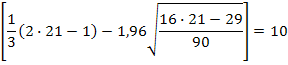
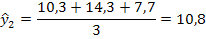
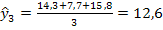 и т.д.
и т.д.
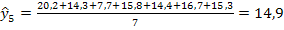 и т.д.
и т.д.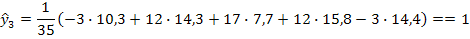
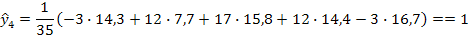
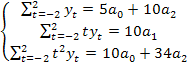 (1.8.53)
(1.8.53)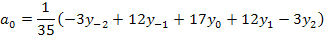

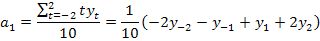
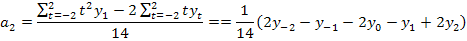
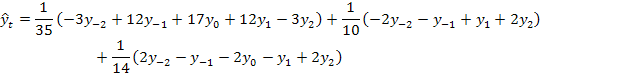
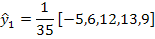
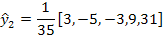
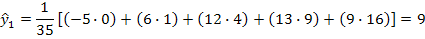
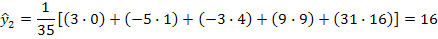
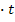
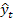

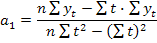
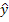 t (графа 5 таблицы1).
t (графа 5 таблицы1).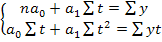 отсюда,
отсюда,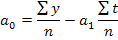
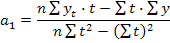
 t .
t .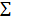 0 1046,66
0 1046,66
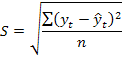
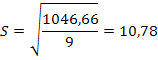
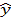 t ±taS
t ±taS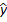 ±10,78 • 2,365 или
±10,78 • 2,365 или  =10 ±25,5или при
=10 ±25,5или при 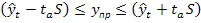
 i
i
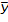 =18,42
=18,42
 ). Затем вычисляется среднемесячный уровень для всего ряда
). Затем вычисляется среднемесячный уровень для всего ряда 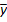 . После чего определяется показатель сезонной волны - индекс сезонности Is как процентное отношение средних для каждого месяца к общему среднемесячному уровню, %.
. После чего определяется показатель сезонной волны - индекс сезонности Is как процентное отношение средних для каждого месяца к общему среднемесячному уровню, %.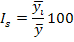
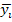 - средний уровень для каждого месяца (за три года);
- средний уровень для каждого месяца (за три года);  2
2
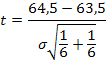

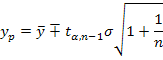
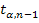 - табличное значение t-критерия Стьюдента при уровне значимости а числе степеней свободы (n-1). Для нашего примера:
- табличное значение t-критерия Стьюдента при уровне значимости а числе степеней свободы (n-1). Для нашего примера: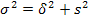
 - межгрупповая дисперсия;
- межгрупповая дисперсия; 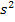 - внутригрупповая
- внутригрупповая
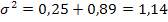 и
и 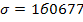
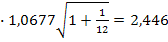
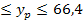

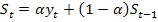 a=0,1 по условию
a=0,1 по условию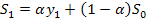

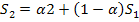
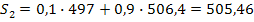
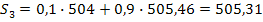
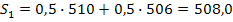
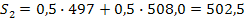
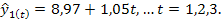
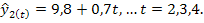
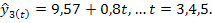
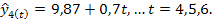
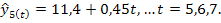
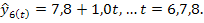
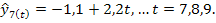
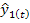 которое получаем из
которое получаем из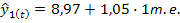
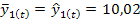
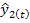 , которые получаем из уравнений:
, которые получаем из уравнений: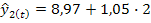
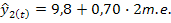
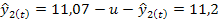
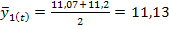

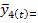 12,68
12,68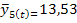
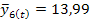

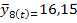
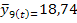
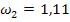
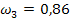
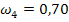
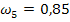
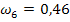
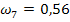
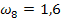
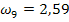
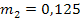
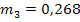
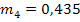
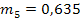
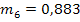
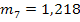
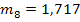
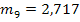
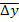 = 1,51) и рассчитаем прогнозные значения производства продукции по формуле 7.33.
= 1,51) и рассчитаем прогнозные значения производства продукции по формуле 7.33.


