
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение общих качественных индексов в агрегатной форме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для построения общих качественных индексов в агрегатной форме следует помнить следующие правила: В индексе изменяется только индексируемая величина и всегда от отчетного периода (в числителе) к базисной (в знаменателе). Вес (соизмеримость) остается неизменным, т.е. одинаковым в числителе и знаменателе (кроме случая, когда индексируемой величиной яачяется все произведение); 2. В индексах качественных показателей индексируемая величина качественный показатель ("х"), а весом является количественный показатель ("d"), который берется неизменным в числителе и знаменателе на уровне отчетного периода ("I");(Исключение индекс производительности труда по трудоемкости) З. При записи сводного индекса на первом месте (первым сомножителем) пишется индексируемая величина (х) а на втором вec (d) (правило не строгое, но необходимое во избежание механических ошибок); 4.Изменение показателя в абсолютном выражении определяется как разность числителя и знаменателя индекса (исключение индекс производительности труда по трудоемкости). Тогда индексы всех качественных индексов (кроме исключения) в общем виде можно записать в виде формулы
Например, конкретный индекс цены: где
отчетного периода, a
характеризует изменение товарооборота (стоимости продукции) за счет цен "+" - увеличение,"-" уменьшение. Исключением является индекс производительности труда по трудоемкости, т.к. трудоемкость - обратный показатель производительности труда и, следовательно, уменьшение затрат труда на единицу продукции означает рост производительности труда. Поэтому индекс производительности труда по трудоемкости определяется по формуле:
а изменение затрат труда определяется как разность знаменателя и числителя индекса, т.е,
изменение затрат труда за счет изменения производительности труда. Построение качественных индексов в форме среднего индекса. Сводный индекс может быть исчислен как средняя величина из индивидуальных индексов. Форма среднего индекса используется в тех случаях, когда в агрегатной форме индекс на основе имеющейся информации рассчитать невозможно. Однако, форму средней для этого' нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу. В практике статистики в большинстве случаев принято все качественные индексы в форме среднего рассчитывать как средние гармонические. Выведем средний гармонический индекс из агрегатного в общем виде.
Т.к. Изменение же явления в абсолютном выражении определяется так же как и в агрегатной форме разностью числителя и знаменателя индекса (исключение индекс производительности труда по трудоемкости).
Аналогично записываются все качественные индексы (кроме исключения). Например, индекс цен:
Изменение же явления в абсолютном выражении
и показывает изменение товарооборота в абсолютном выражении за счет цен. Исключением является индекс производительности труда по трудоемкости.
Он происходит от агрегатного и тождествен ему, исходя из следующих соотношений: Конкретные индексы качественных показателей в агрегатной форе и форме среднего индекса в приложении 1 ( Таблица 1)
Индексы средних величин. Для характеристики динамики средних величии (среднеотраслевой себестоимости определенного вида продукции, средних цен одного вида продукции, средней урожайности одной и той же культуры, средней заработной платы работников одной профессии и так далее используются индексы переменного состава, постоянного (фиксированного) состава и индексы структурных сдвигов. Эти индексы представляют собой отношение двух средних качественных показателей. Динамика средних показателей зависит от одновременного изменения индекс, в котором отражается изменение как индексируемой величины (х), так и структуры (состава) совокупности
называется индексом переменного состава и определяется в обобщенном виде по формуле:
средняя базисная величина при условии отчетной структуры, характеризует изменение только индексируемой величины. Влияние структурных сдвигов на индексируемую величину видно из индекса структурных сдвигов:
Между этими индексами существует взаимосвязь, а именно:
Так, например, изменение средней отраслевой себестоимости какого то вида продукции может происходить не только за счет ее изменения на отдельных предприятиях но и за счет изменения доли выпуска этой продукции в общем объеме ее в отрасли т.е.структуры выпуска. В этом случае изменение средней себестоимости при совместном влиянии двух факторов (себестоимости на каждом предприятии и структуры выпуска) отразит индекс переменного состава:
Влияние на среднюю себестоимость изменения себестоимости на каждом предприятии отразит индекс фиксированного состава:
Как изменилась средняя себестоимость за счет изменения структуры выпуска (доли выпуска на каждом предприятии от уровня отраслевого) покажет индекс структурных сдвигов
Исключением является индекс производительности труда по трудоемкости
Конкретные индексы средних величин в приложении 1 (таблица 3)
Базисные и цепные индексы. При изучении динамики явления за ряд последовательных периодов (лет, месяцев т.д.) рассчитывают ряд индексов. Эти индексы показывают изменение явления либо по отношению к постоянной базе (базисные индексы), либо по отношению к переменной базе (цепные индексы). Цепные и базисные индексы могут быть индивидуальными и общими. Расчет индивидуальных индексов при этом прост, (Для удобства записи отсчет времени начнем с первого периода). Тогда качественные базисные индивидуальные индексы в общем виде
И т.д. а цепные
ит.д. Аналогично рассчитываются и количественные базисные и цепные индивидуальные индексы. Взаимосвязь между ними: произведение цепных индексов равно последнему базисному:
При построении базисных и цепных общих индексов возникает проблема весов. Веса при этом могут быть постоянными (т.е. одинаковыми во всех индексах) и могут быть переменными (т.е. изменяющимися от индекса к индексу). В большинстве случаев принято все общие индексы (базисные и цепные) количественных показателей записывать с постоянными весами. В общем виде это выглядит так:
И т.д. и цепные индексы
и т.д. Взаимосвязь между ними в этом случае сохраняется: произведение цепных индексов равно последнему базисному индексу:
Базисные и цепные индексы качественных показателей в большинстве случаев записываются с переменными весами. В общем виде это будет: базисные индексы:
И т.д. и цепные индексы
и т.д. Между базисными и цепными индексами с переменными весами вышеуказанная взаимосвязь отсутствует. Конкретные базисные и цепные индексы в приложении I (Таблица 2).
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

 (1.9.5)
(1.9.5) (1.9.6)
(1.9.6) - товарооборот (или стоимость произведенной продукции)
- товарооборот (или стоимость произведенной продукции) (1.9.7)
(1.9.7) - - товарооборот (стоимость продукции) отчетного периода в базисных ценах, а разность
- - товарооборот (стоимость продукции) отчетного периода в базисных ценах, а разность
 (1.9.8)
(1.9.8) (8.8) и означает
(8.8) и означает (1.9.9)
(1.9.9) отсюда
отсюда 
 (1.9.10)
(1.9.10)

 (1.9.11)
(1.9.11) ,
, 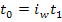 ,
, 

 (1.9.12)
(1.9.12)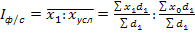 где
где  (1.9.13)
(1.9.13) (1.9.14)
(1.9.14) (1.9.15)
(1.9.15)




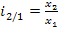 ,
,  ,
,  (1.9.16)
(1.9.16) ,
,  (1.9.17)
(1.9.17) =
= 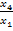 (1.9.18)
(1.9.18) ,
,  ,
,  (1.9.19)
(1.9.19) ,
,  (1.9.20)
(1.9.20) (1.9.21)
(1.9.21) ,
,  ,
,  (1.9.22)
(1.9.22) ,
,  (1.9.23)
(1.9.23)


